北师大版九年级数学上册3.1用树状图或表格求概率 课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级数学上册3.1用树状图或表格求概率 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 187.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第三章
概率的进一步认识
3.1
用树状图或表格求概率
生活中,有些事情我们先能肯定它一定会发生,这些事情称为
有些事情我们先能肯定它一定不会发生,这些事情称为
有些事情我们事先无法肯定它会不会发生,这些事情称为
必然事件
不可能事件
不确定事件
一、复习回顾
1.
概率是研究大量同类随机现象的统计规律的数学学科。
概率是随机事件发生的可能性的数量指标。
在独立随机事件中,如果某一事件在全部事件中出现的频率,在更大的范围内比较明显地稳定在某一固定常数附近,就可以认为这个事件发生的概率为这个常数。
对于任何事件的概率值一定介于
0
和
1
之间。
0
≤
概率值P
≤
1
一、复习回顾
2.
概率的计算:
一般地,若一件实验中所有可能结果出现的可能性是一样,那么事件A发生的概率为
P(A)=
事件A可能出现的结果数
所有可能出现的结果数
3.
求事件发生的常用一种方法就是将所有可能的结果都列出来,然后计算所有可能出现的结果总数及事件中A可能出现的结果数,从而求出所求事件的概率。
4.
在求概率时,我们可用“树状图”或“列表法”来帮助分析。
一、复习回顾
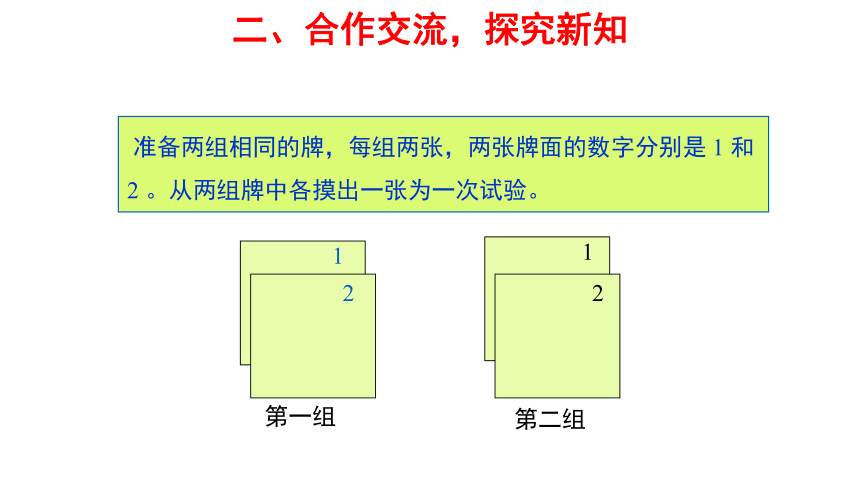
准备两组相同的牌,每组两张,两张牌面的数字分别是
1
和
2
。从两组牌中各摸出一张为一次试验。
1
2
1
2
第一组
第二组
二、合作交流,探究新知
两步试验
对于摸牌游戏,在一次试验中,如果摸得第一张牌的牌面数字为
1
,那么摸第二张牌时,摸得牌面数字为几的可能性大?
如果摸得第一张牌的牌面数字为
2
呢?
根据你所做的
30
次试验的记录,分别统计一下,摸得第一张牌的牌面数字为
1
时,摸第二张牌的牌面数字为
1
和
2
的次数。
二、合作交流,探究新知
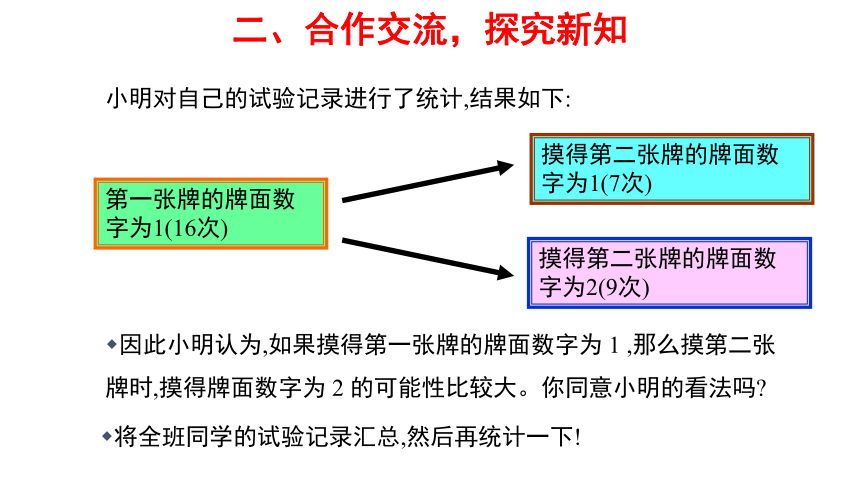
小明对自己的试验记录进行了统计,结果如下:
因此小明认为,如果摸得第一张牌的牌面数字为
1
,那么摸第二张牌时,摸得牌面数字为
2
的可能性比较大。你同意小明的看法吗?
将全班同学的试验记录汇总,然后再统计一下!
第一张牌的牌面数字为1(16次)
摸得第二张牌的牌面数字为1(7次)
摸得第二张牌的牌面数字为2(9次)
二、合作交流,探究新知
事实上,在一次试验中,不管摸得第一张牌的牌面数字为几,摸第二张牌时,摸得牌面数字为
1
和
2
的可能性是相同的。
概率的等可能性
二、合作交流,探究新知
对于前面的摸牌游戏,一次试验中会出现哪些可能的结果?每种结果出现的可能性相同吗?
频率的等可能性如何表示?
会出现三种可能的结果:牌面数字和为
2,
牌面数字和为
3,
牌面数字和为
4;
每种结果出现的可能性相同。
二、合作交流,探究新知
我与他的结果不同:
对此你有什么评论?
会出现四种可能的结果:牌面数字为(1
,
1),牌面数字为(1
,
2),牌面数字为(2
,
1),牌面数字为(2
,
2)。
每种结果出现的可能性相同。
二、合作交流,探究新知
(一)用树状图表示概率
实际上,摸第一张牌时,可能出现的结果是:牌面数字为
1
或
2,
而且这两种结果出现的可能性相同;摸第二张牌时,情况也是如此。因此,我们可以用右面的树状图或下面的表格来表示所有可能出现的结果:
开始
第一张牌的牌面数字
1
2
第二张牌的牌面数字
1
2
1
2
所有可能出现的结果
(1
,
1)
(1
,
2)
(2
,
1)
(2
,
2)
二、合作交流,探究新知
从上面的树状图或表格可以看出,一次试验可能出现的结果共有
4
种:(1
,
1),
(1
,
2),
(2
,
1),
(2
,
2),
而且每种结果出现的可能性相同。也就是说,每种结果出现的概率都是
1/4。
老师提示:
利用树状图或表格可以较方便地求出某些事件发生的概率。
(二)用表格表示概率
第二张牌的牌面数字
第一张牌的牌面数字
1
1
2
(1
,
1)
(1
,
2)
2
(2
,
1)
(2
,
2)
二、合作交流,探究新知
例1
随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?
总共有
4
种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有
3
种:(正
,
正),
(正
,
反),
(反
,
正),
因此至少有一次正面朝上的概率是
3/4。
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
三、运用新知
例2
袋中装有四个红色球和两个兰色球,它们除了颜色外都相同;
(1)随机从中摸出一球,恰为红球的概率是
;
(2)随机从中摸出一球,记录下颜色后放回袋中,充分混合后再随机摸出一球,两次都摸到红球的概率为
;
(3)随机从中一次摸出两个球,两球均为红球的概率是
。
三、运用新知
分析
(1)随机从中摸出一球,恰为红球的概率是
;
袋中一共有
6
个球,红球有
4
个,所以随机摸一个,摸到红球的概率是
4/6,也就是
2/3。
2/3
三、运用新知
(2)随机从中摸出一球,记录下颜色后放回袋中,充分混合后再随机摸出一球,两次都摸到红球的概率为
;
红球
红球
红球
红球
兰球
兰球
1
2
3
4
5
6
分析
三、运用新知
分析
第二次摸球号
第一次摸球号
1
2
3
4
5
6
1
2
3
4
6
5
(1,1)
(1,2)
(2,1)
(2,2)
(1,3)
(2,3)
(3,1)
(3,2)
(3,3)
(1,4)
(1,5)
(1,6)
(2,4)
(2,5)
(2,6)
(3,6)
(3,5)
(3,4)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(5,6)
(4,6)
(6,6)
(5,5)
(6,5)
(5,4)
(6,4)
(5,3)
(6,3)
(5,2)
(6,2)
(5,1)
(6,1)
两次都摸到红球的概率为
_______。
4/9
三、运用新知
(3)随机从中一次摸出两个球,两球均为红球的概率是
。
红球
红球
红球
红球
兰球
兰球
1
2
3
4
5
6
分析
三、运用新知
第二次摸球号
第一次摸球号
1
2
3
4
5
6
1
2
3
4
6
5
(1,1)
(1,2)
(2,1)
(2,2)
(1,3)
(2,3)
(3,1)
(3,2)
(3,3)
(1,4)
(1,5)
(1,6)
(2,4)
(2,5)
(2,6)
(3,6)
(3,5)
(3,4)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(5,6)
(4,6)
(6,6)
(5,5)
(6,5)
(5,4)
(6,4)
(5,3)
(6,3)
(5,2)
(6,2)
(5,1)
(6,1)
两球均为红球的概率为
_______。
2/5
分析
三、运用新知
四、归纳小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率。
用树状图或表格表示概率。
再
见
第三章
概率的进一步认识
3.1
用树状图或表格求概率
生活中,有些事情我们先能肯定它一定会发生,这些事情称为
有些事情我们先能肯定它一定不会发生,这些事情称为
有些事情我们事先无法肯定它会不会发生,这些事情称为
必然事件
不可能事件
不确定事件
一、复习回顾
1.
概率是研究大量同类随机现象的统计规律的数学学科。
概率是随机事件发生的可能性的数量指标。
在独立随机事件中,如果某一事件在全部事件中出现的频率,在更大的范围内比较明显地稳定在某一固定常数附近,就可以认为这个事件发生的概率为这个常数。
对于任何事件的概率值一定介于
0
和
1
之间。
0
≤
概率值P
≤
1
一、复习回顾
2.
概率的计算:
一般地,若一件实验中所有可能结果出现的可能性是一样,那么事件A发生的概率为
P(A)=
事件A可能出现的结果数
所有可能出现的结果数
3.
求事件发生的常用一种方法就是将所有可能的结果都列出来,然后计算所有可能出现的结果总数及事件中A可能出现的结果数,从而求出所求事件的概率。
4.
在求概率时,我们可用“树状图”或“列表法”来帮助分析。
一、复习回顾
准备两组相同的牌,每组两张,两张牌面的数字分别是
1
和
2
。从两组牌中各摸出一张为一次试验。
1
2
1
2
第一组
第二组
二、合作交流,探究新知
两步试验
对于摸牌游戏,在一次试验中,如果摸得第一张牌的牌面数字为
1
,那么摸第二张牌时,摸得牌面数字为几的可能性大?
如果摸得第一张牌的牌面数字为
2
呢?
根据你所做的
30
次试验的记录,分别统计一下,摸得第一张牌的牌面数字为
1
时,摸第二张牌的牌面数字为
1
和
2
的次数。
二、合作交流,探究新知
小明对自己的试验记录进行了统计,结果如下:
因此小明认为,如果摸得第一张牌的牌面数字为
1
,那么摸第二张牌时,摸得牌面数字为
2
的可能性比较大。你同意小明的看法吗?
将全班同学的试验记录汇总,然后再统计一下!
第一张牌的牌面数字为1(16次)
摸得第二张牌的牌面数字为1(7次)
摸得第二张牌的牌面数字为2(9次)
二、合作交流,探究新知
事实上,在一次试验中,不管摸得第一张牌的牌面数字为几,摸第二张牌时,摸得牌面数字为
1
和
2
的可能性是相同的。
概率的等可能性
二、合作交流,探究新知
对于前面的摸牌游戏,一次试验中会出现哪些可能的结果?每种结果出现的可能性相同吗?
频率的等可能性如何表示?
会出现三种可能的结果:牌面数字和为
2,
牌面数字和为
3,
牌面数字和为
4;
每种结果出现的可能性相同。
二、合作交流,探究新知
我与他的结果不同:
对此你有什么评论?
会出现四种可能的结果:牌面数字为(1
,
1),牌面数字为(1
,
2),牌面数字为(2
,
1),牌面数字为(2
,
2)。
每种结果出现的可能性相同。
二、合作交流,探究新知
(一)用树状图表示概率
实际上,摸第一张牌时,可能出现的结果是:牌面数字为
1
或
2,
而且这两种结果出现的可能性相同;摸第二张牌时,情况也是如此。因此,我们可以用右面的树状图或下面的表格来表示所有可能出现的结果:
开始
第一张牌的牌面数字
1
2
第二张牌的牌面数字
1
2
1
2
所有可能出现的结果
(1
,
1)
(1
,
2)
(2
,
1)
(2
,
2)
二、合作交流,探究新知
从上面的树状图或表格可以看出,一次试验可能出现的结果共有
4
种:(1
,
1),
(1
,
2),
(2
,
1),
(2
,
2),
而且每种结果出现的可能性相同。也就是说,每种结果出现的概率都是
1/4。
老师提示:
利用树状图或表格可以较方便地求出某些事件发生的概率。
(二)用表格表示概率
第二张牌的牌面数字
第一张牌的牌面数字
1
1
2
(1
,
1)
(1
,
2)
2
(2
,
1)
(2
,
2)
二、合作交流,探究新知
例1
随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?
总共有
4
种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有
3
种:(正
,
正),
(正
,
反),
(反
,
正),
因此至少有一次正面朝上的概率是
3/4。
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
三、运用新知
例2
袋中装有四个红色球和两个兰色球,它们除了颜色外都相同;
(1)随机从中摸出一球,恰为红球的概率是
;
(2)随机从中摸出一球,记录下颜色后放回袋中,充分混合后再随机摸出一球,两次都摸到红球的概率为
;
(3)随机从中一次摸出两个球,两球均为红球的概率是
。
三、运用新知
分析
(1)随机从中摸出一球,恰为红球的概率是
;
袋中一共有
6
个球,红球有
4
个,所以随机摸一个,摸到红球的概率是
4/6,也就是
2/3。
2/3
三、运用新知
(2)随机从中摸出一球,记录下颜色后放回袋中,充分混合后再随机摸出一球,两次都摸到红球的概率为
;
红球
红球
红球
红球
兰球
兰球
1
2
3
4
5
6
分析
三、运用新知
分析
第二次摸球号
第一次摸球号
1
2
3
4
5
6
1
2
3
4
6
5
(1,1)
(1,2)
(2,1)
(2,2)
(1,3)
(2,3)
(3,1)
(3,2)
(3,3)
(1,4)
(1,5)
(1,6)
(2,4)
(2,5)
(2,6)
(3,6)
(3,5)
(3,4)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(5,6)
(4,6)
(6,6)
(5,5)
(6,5)
(5,4)
(6,4)
(5,3)
(6,3)
(5,2)
(6,2)
(5,1)
(6,1)
两次都摸到红球的概率为
_______。
4/9
三、运用新知
(3)随机从中一次摸出两个球,两球均为红球的概率是
。
红球
红球
红球
红球
兰球
兰球
1
2
3
4
5
6
分析
三、运用新知
第二次摸球号
第一次摸球号
1
2
3
4
5
6
1
2
3
4
6
5
(1,1)
(1,2)
(2,1)
(2,2)
(1,3)
(2,3)
(3,1)
(3,2)
(3,3)
(1,4)
(1,5)
(1,6)
(2,4)
(2,5)
(2,6)
(3,6)
(3,5)
(3,4)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(5,6)
(4,6)
(6,6)
(5,5)
(6,5)
(5,4)
(6,4)
(5,3)
(6,3)
(5,2)
(6,2)
(5,1)
(6,1)
两球均为红球的概率为
_______。
2/5
分析
三、运用新知
四、归纳小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率。
用树状图或表格表示概率。
再
见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
