人教版八年级数学上册 13.2 轴对称图形 同步提高训练(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 13.2 轴对称图形 同步提高训练(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 839.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 20:55:16 | ||
图片预览


文档简介
人教版八年级数学上册
13.2
轴对称图形
同步练习(含答案)
一、选择题(本大题共7道小题)
1.
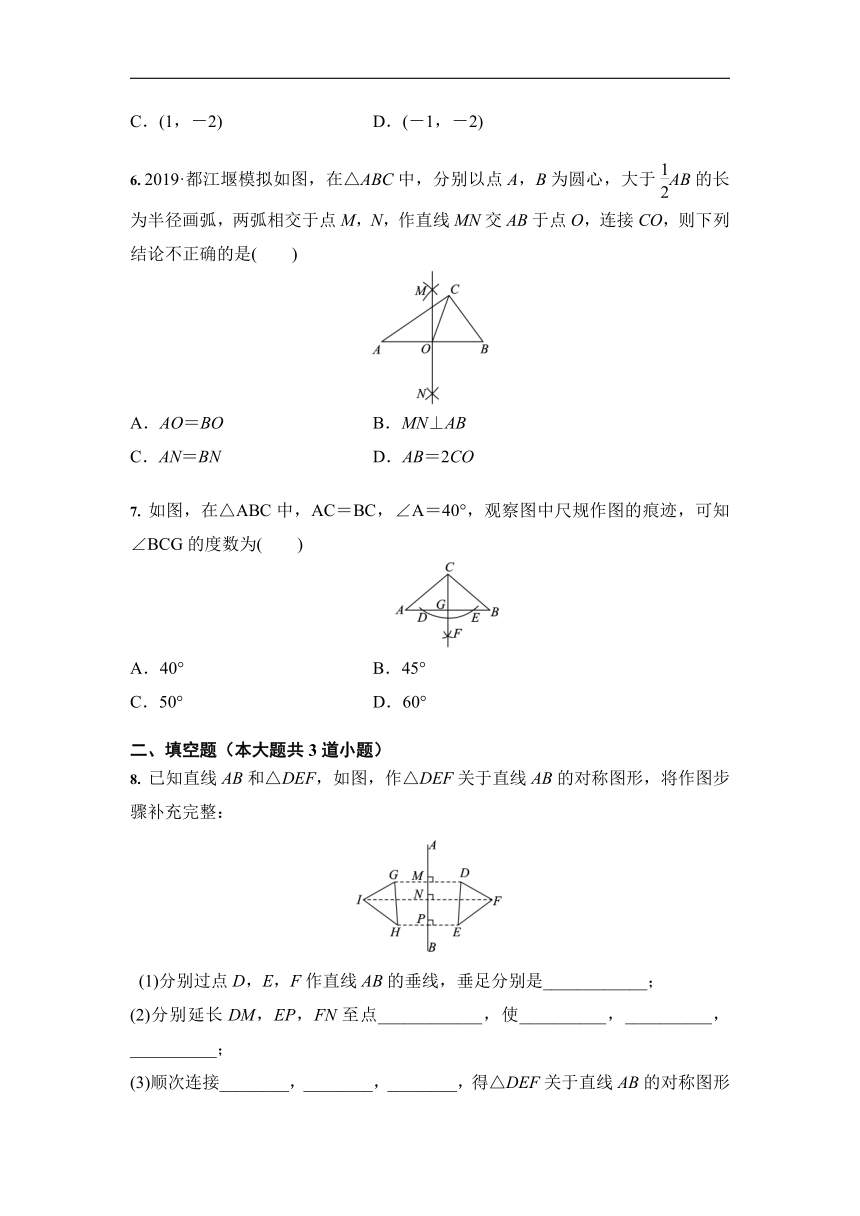
下列轴对称图形中,只有一条对称轴的图形是( )
2.
下列作图,是作点A关于直线l的对称点B的是( )
3.
下列作图,最有可能是作线段AB关于直线l的对称线段A′B′的是( )
4.
如图,长方形的一条对称轴是( )
A.直线l1
B.直线l2
C.直线l3
D.直线l4
5.
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则她放的位置是( )
A.(-2,1)
B.(-1,1)
C.(1,-2)
D.(-1,-2)
6.
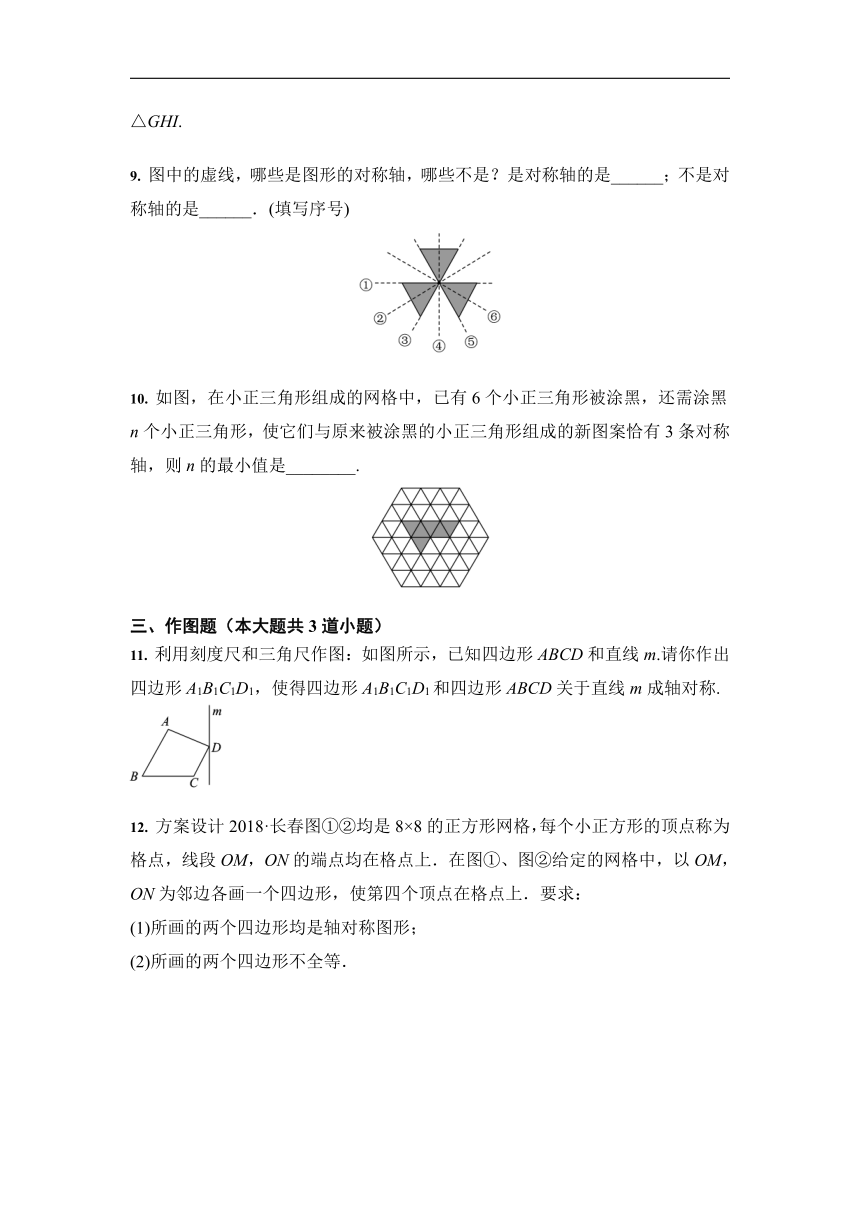
2019·都江堰模拟如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则下列结论不正确的是( )
A.AO=BO
B.MN⊥AB
C.AN=BN
D.AB=2CO
7.
如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
A.40°
B.45°
C.50°
D.60°
二、填空题(本大题共3道小题)
8.
已知直线AB和△DEF,如图,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
(1)分别过点D,E,F作直线AB的垂线,垂足分别是____________;
(2)分别延长DM,EP,FN至点____________,使__________,__________,__________;
(3)顺次连接________,________,________,得△DEF关于直线AB的对称图形△GHI.
9.
图中的虚线,哪些是图形的对称轴,哪些不是?是对称轴的是______;不是对称轴的是______.(填写序号)
10.
如图,在小正三角形组成的网格中,已有6个小正三角形被涂黑,还需涂黑n个小正三角形,使它们与原来被涂黑的小正三角形组成的新图案恰有3条对称轴,则n的最小值是________.
三、作图题(本大题共3道小题)
11.
利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.
12.
方案设计2018·长春图①②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM,ON的端点均在格点上.在图①、图②给定的网格中,以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
(1)所画的两个四边形均是轴对称图形;
(2)所画的两个四边形不全等.
13.
(1)在图①中,CA=CB,CM=CN,请用无刻度的直尺画出△ABC的对称轴;
(2)在图②中,已知正五边形ABCDE,请用无刻度的直尺画出它的一条对称轴.
四、解答题(本大题共3道小题)
14.
如图,△ABC在正方形网格中.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)若网格中的最小正方形的边长为1,求△ABC的面积.
15.
请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
16.
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出与△ABC关于y轴对称的△A2B2C2;
(3)请写出点A1,A2的坐标.
人教版八年级数学上册
13.2
轴对称图形
同步练习-答案
一、选择题(本大题共7道小题)
1.
【答案】C [解析]
选项A有三条对称轴,选项B有五条对称轴,选项D有两条对称轴,只有选项C仅有一条对称轴.
2.
【答案】C
3.
【答案】B
4.
【答案】B
5.
【答案】B [解析]
根据方子的位置可知对称轴是从左上斜向下的对角线所在的直线,由此可知第4枚圆子应放入棋盘(-1,1)的位置.故选B.
6.
【答案】D [解析]
由作法得MN垂直平分AB,
∴OA=OB,MN⊥AB,AN=BN,只有选项D不成立.
7.
【答案】C [解析]
由作法得CG⊥AB.
∵AC=BC,∴CG平分∠ACB,∠A=∠B=40°.
∵∠ACB=180°-∠A-∠B=100°,
∴∠BCG=∠ACB=50°.
二、填空题(本大题共3道小题)
8.
【答案】(1)M,P,N
(2)G,H,I MG=DM PH=EP NI=FN
(3)GH HI IG
9.
【答案】②④⑥ ①③⑤
10.
【答案】3 [解析]
如图所示,n的最小值为3.
三、作图题(本大题共3道小题)
11.
【答案】
解:如图,四边形A1B1C1D1即为所求.
12.
【答案】
如图所示:
13.
【答案】
解:(1)如图①,直线CD即为所求.
(2)答案不唯一,如图②,直线OA即为所求.
四、解答题(本大题共3道小题)
14.
【答案】
解:(1)如图,分别作点A,B,C关于直线MN的对称点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
(2)如图,S△ABC=S长方形DECF-S△ABD-S△BEC-S△AFC=2×3-2×-×1×3=6-2-=.
15.
【答案】
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
16.
【答案】
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
(3)A1(2,3),A2(-2,-1).
13.2
轴对称图形
同步练习(含答案)
一、选择题(本大题共7道小题)
1.
下列轴对称图形中,只有一条对称轴的图形是( )
2.
下列作图,是作点A关于直线l的对称点B的是( )
3.
下列作图,最有可能是作线段AB关于直线l的对称线段A′B′的是( )
4.
如图,长方形的一条对称轴是( )
A.直线l1
B.直线l2
C.直线l3
D.直线l4
5.
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则她放的位置是( )
A.(-2,1)
B.(-1,1)
C.(1,-2)
D.(-1,-2)
6.
2019·都江堰模拟如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则下列结论不正确的是( )
A.AO=BO
B.MN⊥AB
C.AN=BN
D.AB=2CO
7.
如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
A.40°
B.45°
C.50°
D.60°
二、填空题(本大题共3道小题)
8.
已知直线AB和△DEF,如图,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
(1)分别过点D,E,F作直线AB的垂线,垂足分别是____________;
(2)分别延长DM,EP,FN至点____________,使__________,__________,__________;
(3)顺次连接________,________,________,得△DEF关于直线AB的对称图形△GHI.
9.
图中的虚线,哪些是图形的对称轴,哪些不是?是对称轴的是______;不是对称轴的是______.(填写序号)
10.
如图,在小正三角形组成的网格中,已有6个小正三角形被涂黑,还需涂黑n个小正三角形,使它们与原来被涂黑的小正三角形组成的新图案恰有3条对称轴,则n的最小值是________.
三、作图题(本大题共3道小题)
11.
利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.
12.
方案设计2018·长春图①②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM,ON的端点均在格点上.在图①、图②给定的网格中,以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
(1)所画的两个四边形均是轴对称图形;
(2)所画的两个四边形不全等.
13.
(1)在图①中,CA=CB,CM=CN,请用无刻度的直尺画出△ABC的对称轴;
(2)在图②中,已知正五边形ABCDE,请用无刻度的直尺画出它的一条对称轴.
四、解答题(本大题共3道小题)
14.
如图,△ABC在正方形网格中.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)若网格中的最小正方形的边长为1,求△ABC的面积.
15.
请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
16.
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出与△ABC关于y轴对称的△A2B2C2;
(3)请写出点A1,A2的坐标.
人教版八年级数学上册
13.2
轴对称图形
同步练习-答案
一、选择题(本大题共7道小题)
1.
【答案】C [解析]
选项A有三条对称轴,选项B有五条对称轴,选项D有两条对称轴,只有选项C仅有一条对称轴.
2.
【答案】C
3.
【答案】B
4.
【答案】B
5.
【答案】B [解析]
根据方子的位置可知对称轴是从左上斜向下的对角线所在的直线,由此可知第4枚圆子应放入棋盘(-1,1)的位置.故选B.
6.
【答案】D [解析]
由作法得MN垂直平分AB,
∴OA=OB,MN⊥AB,AN=BN,只有选项D不成立.
7.
【答案】C [解析]
由作法得CG⊥AB.
∵AC=BC,∴CG平分∠ACB,∠A=∠B=40°.
∵∠ACB=180°-∠A-∠B=100°,
∴∠BCG=∠ACB=50°.
二、填空题(本大题共3道小题)
8.
【答案】(1)M,P,N
(2)G,H,I MG=DM PH=EP NI=FN
(3)GH HI IG
9.
【答案】②④⑥ ①③⑤
10.
【答案】3 [解析]
如图所示,n的最小值为3.
三、作图题(本大题共3道小题)
11.
【答案】
解:如图,四边形A1B1C1D1即为所求.
12.
【答案】
如图所示:
13.
【答案】
解:(1)如图①,直线CD即为所求.
(2)答案不唯一,如图②,直线OA即为所求.
四、解答题(本大题共3道小题)
14.
【答案】
解:(1)如图,分别作点A,B,C关于直线MN的对称点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
(2)如图,S△ABC=S长方形DECF-S△ABD-S△BEC-S△AFC=2×3-2×-×1×3=6-2-=.
15.
【答案】
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
16.
【答案】
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
(3)A1(2,3),A2(-2,-1).
