人教版八年级数学上册11.2.1三角形的内角和定理 课件 (共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册11.2.1三角形的内角和定理 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 104.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 20:55:37 | ||
图片预览





文档简介
(共20张PPT)
三角形内角和定理
为什么要证明
观察、试验可以发现规律,但下结论缺乏说服力,三角形的个数无限多个,只有通过理由充足的推理论证,才能得出让人们信服的结论,这种推理的过程就叫证明。
证明文字命题的步骤:根据题意画图形、写已知、求证、进行分析、写出证明过程。
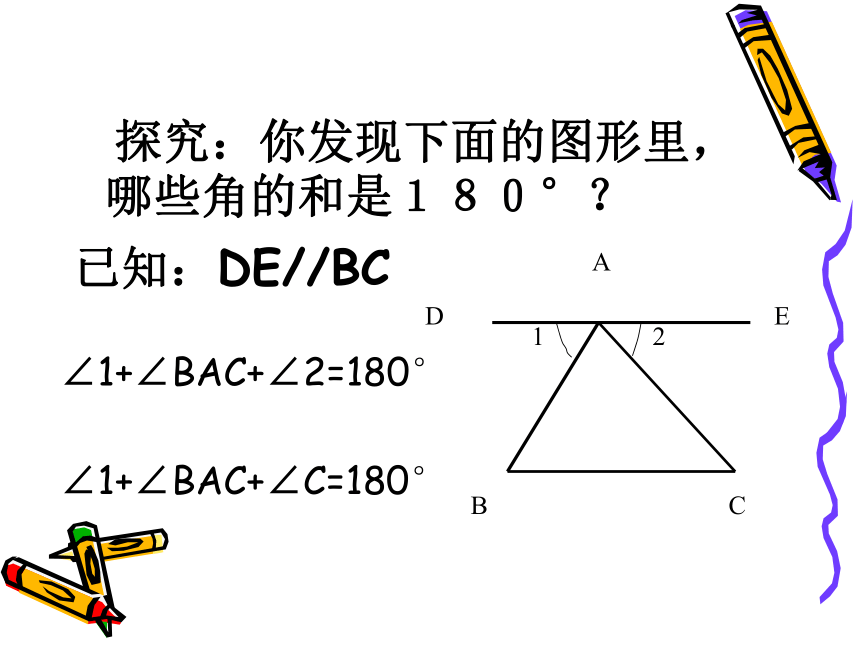
探究:你发现下面的图形里,哪些角的和是180°?
已知:DE//BC
B
D
C
A
E
1
2
∠1+∠BAC+∠2=180°
∠1+∠BAC+∠C=180°
探究发现:
可以得到180°的角有下列情况:
(1)平角、邻补角的度数是180°
(2)两直线平行,同旁内角的和
是180°。
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。
在平面几何里,辅助线通常画成虚线。
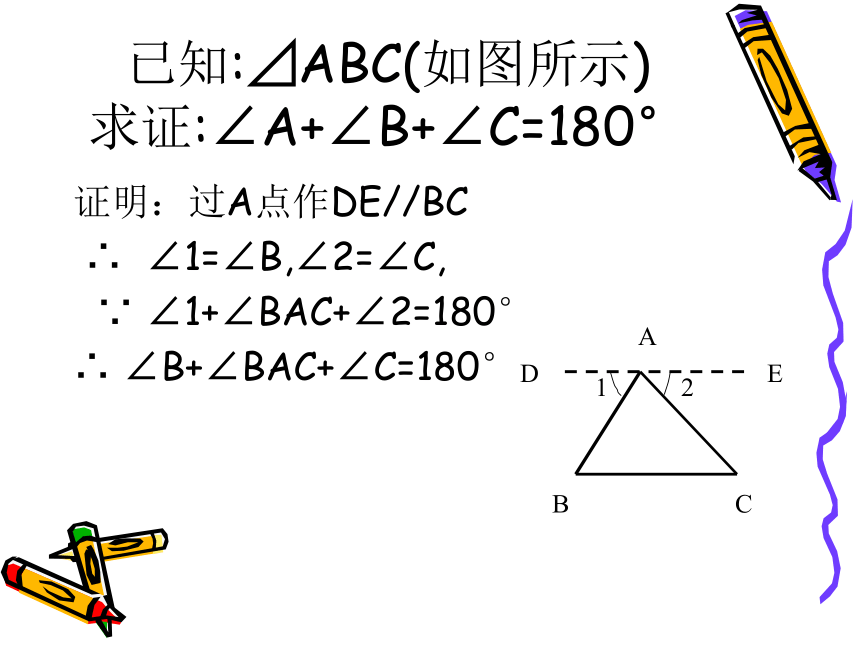
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:过A点作DE//BC
∴
∠1=∠B,∠2=∠C,
∵
∠1+∠BAC+∠2=180°
∴
∠B+∠BAC+∠C=180°
B
D
C
A
E
1
2
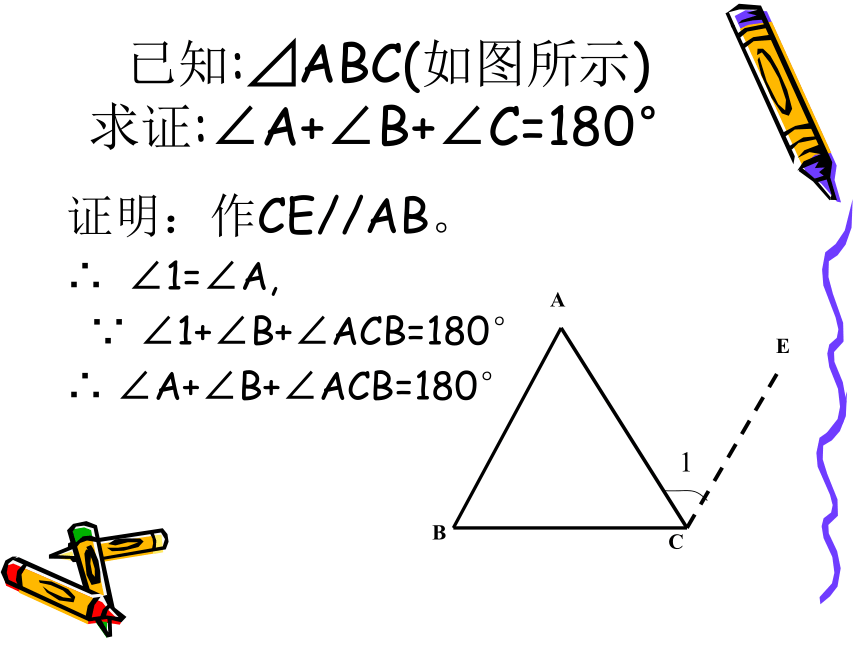
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:作CE//AB。
∴
∠1=∠A,
∵
∠1+∠B+∠ACB=180°
∴
∠A+∠B+∠ACB=180°
C
B
A
E
1
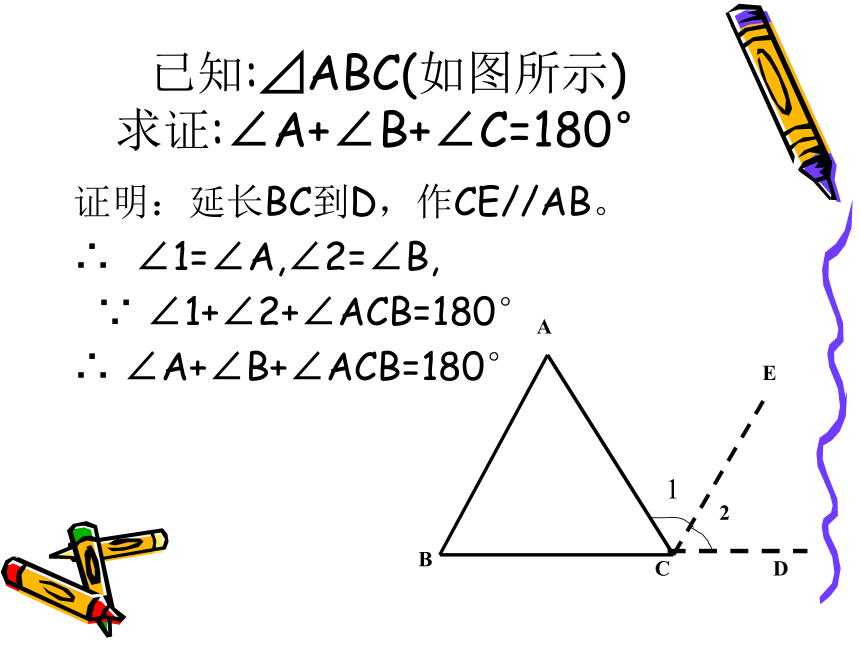
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:延长BC到D,作CE//AB。
∴
∠1=∠A,∠2=∠B,
∵
∠1+∠2+∠ACB=180°
∴
∠A+∠B+∠ACB=180°
C
B
A
E
1
2
D
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:作AD⊥BC,BE
⊥
BC,CF
⊥
BC。
A
B
C
D
F
E
1
3
2
4
证明:过BC上任意一点D,
作DE//AC,DF//AB,
B
D
C
A
F
E
3
5
2
4
1
思路总结:
证明三角形内角和等于180°,关键是:添加辅助线,通过平行线来移动三角形的角,把它们转化成我们熟悉的图形,如
(1)一个平角;
(2)平行线的同旁内角;
(3)两个直角之和;
或者用其它方法,把新知识转化为旧知识,最后解决问题。
转化思想是数学中的常用方法.
例21、如图,在△ABC中,∠BAC=40°,∠B=75°,
AD是∠
BAC的角平分线.求∠ADB的度数.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=
180°-75°-20°
=85°
C
A
B
D
75°
40°
解:∵
AD是∠
BAC的角平分线,
例2
如图3,C岛在A岛的北偏东50度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西40度方向,从C岛看A、B两岛的视角∠ACB是多少度?
A
B
北
E
C
D
北
分析:
已知:AD//BE,
,
∠DAC=50°,∠DAB=80°,
∠EBC=40°
求:∠C=?
E
A
B
北
C
D
北
50°
80°
40°
解:∵∠CAD=50°,∠DAB=80°
∴
∠BAC=∠BAD-∠CAD=30°
∵AD//BE,∠DAB=80°
∴
∠ABE=180°-∠DAB=100°
∵
∠EBC=40°∴
∠ABC=60°
∴
∠ACB=180°-∠ABC-∠BAC=90°
答:从C岛看A、B两岛的视角∠ACB
是90°.
解:作CF//AD,
∵AD//BE,∴CF//AD,
∴∠ACF=∠DAC,∠BCF=∠EBC.
∵
∠DAC=50
°,
∠EBC=40°,
∴∠ACB=
∠DAC+∠EBC=90°.
A
B
北
E
C
D
北
F
解:过C点作MN⊥AD,
∴∠AMC=
90°,
∵AD//BE,
∴∠BNC=
90°,
∵
∠DAC=50
°,
∠EBC=40°,
∴
∠ACM=40°
∠BCN=
50
°,
∴∠ACB=
180°-(
∠ACM+∠BCN)=90°.
北
A
B
E
C
D
北
M
N
解:延长AC交BE于F,
∵AD//BE,
∠DAC=50
°,
∴
∠DAC=∠BFC=
50
°,
∵∠EBC=40°,
∴∠FCB=
∠ACB=90°.
C
A
B
D
F
E
北
北
小结
1.为什么要证明?
2.学会三角形内角和的多种证明方法。
3.应用三角形内角和定理解决一些问题。
4.学会正确添加辅助线。
谢谢大家!
敬请指教!
三角形内角和定理
为什么要证明
观察、试验可以发现规律,但下结论缺乏说服力,三角形的个数无限多个,只有通过理由充足的推理论证,才能得出让人们信服的结论,这种推理的过程就叫证明。
证明文字命题的步骤:根据题意画图形、写已知、求证、进行分析、写出证明过程。
探究:你发现下面的图形里,哪些角的和是180°?
已知:DE//BC
B
D
C
A
E
1
2
∠1+∠BAC+∠2=180°
∠1+∠BAC+∠C=180°
探究发现:
可以得到180°的角有下列情况:
(1)平角、邻补角的度数是180°
(2)两直线平行,同旁内角的和
是180°。
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。
在平面几何里,辅助线通常画成虚线。
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:过A点作DE//BC
∴
∠1=∠B,∠2=∠C,
∵
∠1+∠BAC+∠2=180°
∴
∠B+∠BAC+∠C=180°
B
D
C
A
E
1
2
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:作CE//AB。
∴
∠1=∠A,
∵
∠1+∠B+∠ACB=180°
∴
∠A+∠B+∠ACB=180°
C
B
A
E
1
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:延长BC到D,作CE//AB。
∴
∠1=∠A,∠2=∠B,
∵
∠1+∠2+∠ACB=180°
∴
∠A+∠B+∠ACB=180°
C
B
A
E
1
2
D
已知:⊿ABC(如图所示)
求证:∠A+∠B+∠C=180°
证明:作AD⊥BC,BE
⊥
BC,CF
⊥
BC。
A
B
C
D
F
E
1
3
2
4
证明:过BC上任意一点D,
作DE//AC,DF//AB,
B
D
C
A
F
E
3
5
2
4
1
思路总结:
证明三角形内角和等于180°,关键是:添加辅助线,通过平行线来移动三角形的角,把它们转化成我们熟悉的图形,如
(1)一个平角;
(2)平行线的同旁内角;
(3)两个直角之和;
或者用其它方法,把新知识转化为旧知识,最后解决问题。
转化思想是数学中的常用方法.
例21、如图,在△ABC中,∠BAC=40°,∠B=75°,
AD是∠
BAC的角平分线.求∠ADB的度数.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=
180°-75°-20°
=85°
C
A
B
D
75°
40°
解:∵
AD是∠
BAC的角平分线,
例2
如图3,C岛在A岛的北偏东50度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西40度方向,从C岛看A、B两岛的视角∠ACB是多少度?
A
B
北
E
C
D
北
分析:
已知:AD//BE,
,
∠DAC=50°,∠DAB=80°,
∠EBC=40°
求:∠C=?
E
A
B
北
C
D
北
50°
80°
40°
解:∵∠CAD=50°,∠DAB=80°
∴
∠BAC=∠BAD-∠CAD=30°
∵AD//BE,∠DAB=80°
∴
∠ABE=180°-∠DAB=100°
∵
∠EBC=40°∴
∠ABC=60°
∴
∠ACB=180°-∠ABC-∠BAC=90°
答:从C岛看A、B两岛的视角∠ACB
是90°.
解:作CF//AD,
∵AD//BE,∴CF//AD,
∴∠ACF=∠DAC,∠BCF=∠EBC.
∵
∠DAC=50
°,
∠EBC=40°,
∴∠ACB=
∠DAC+∠EBC=90°.
A
B
北
E
C
D
北
F
解:过C点作MN⊥AD,
∴∠AMC=
90°,
∵AD//BE,
∴∠BNC=
90°,
∵
∠DAC=50
°,
∠EBC=40°,
∴
∠ACM=40°
∠BCN=
50
°,
∴∠ACB=
180°-(
∠ACM+∠BCN)=90°.
北
A
B
E
C
D
北
M
N
解:延长AC交BE于F,
∵AD//BE,
∠DAC=50
°,
∴
∠DAC=∠BFC=
50
°,
∵∠EBC=40°,
∴∠FCB=
∠ACB=90°.
C
A
B
D
F
E
北
北
小结
1.为什么要证明?
2.学会三角形内角和的多种证明方法。
3.应用三角形内角和定理解决一些问题。
4.学会正确添加辅助线。
谢谢大家!
敬请指教!
