人教版八年级数学上册12.3 角的平分线性质的应用 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.3 角的平分线性质的应用 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 248.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 11:45:56 | ||
图片预览

文档简介
(共20张PPT)
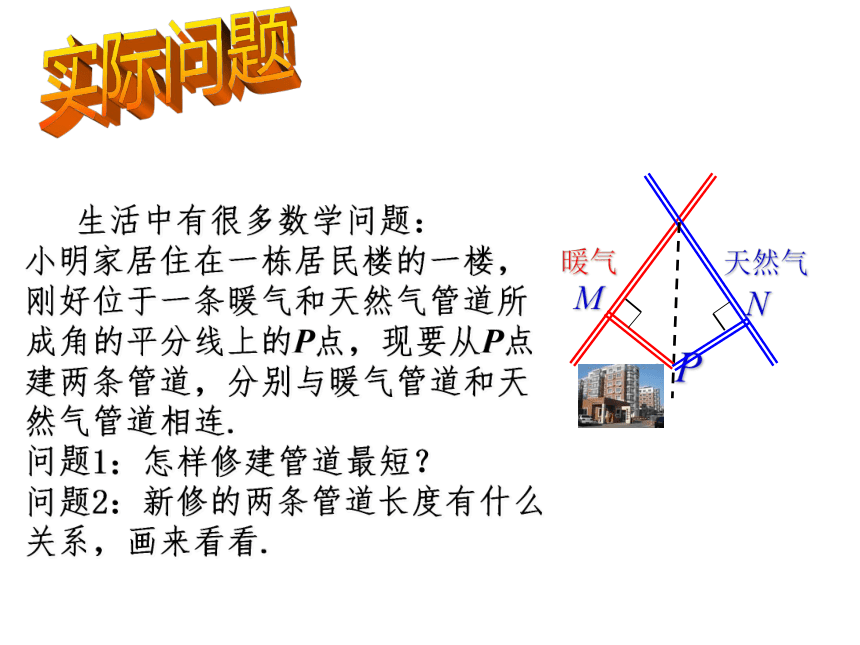
O
A
B
N
M
C
角平分线性质的应用
.
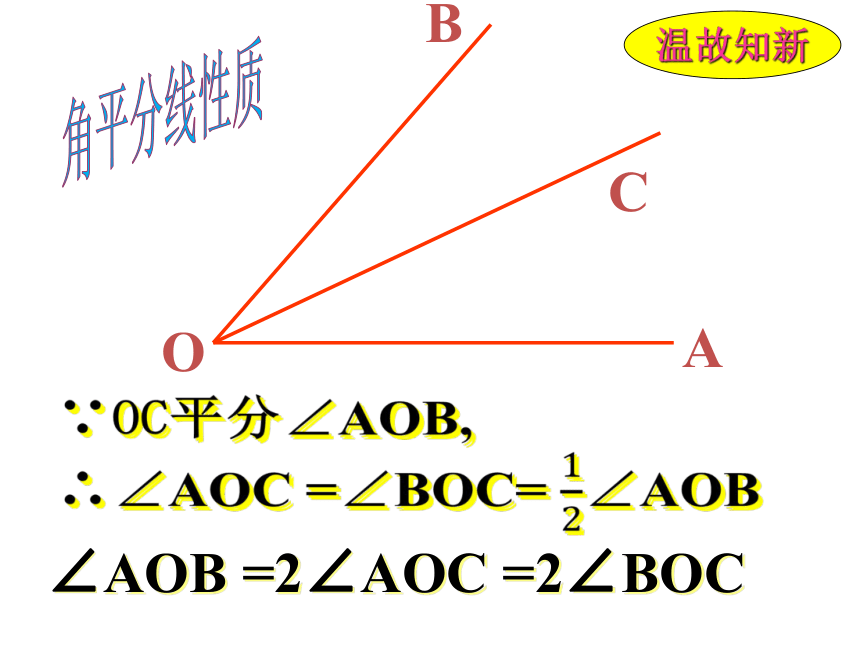
P
暖气
天然气
M
N
实际问题
生活中有很多数学问题:
小明家居住在一栋居民楼的一楼,刚好位于一条暖气和天然气管道所成角的平分线上的P点,现要从P点建两条管道,分别与暖气管道和天然气管道相连.
问题1:怎样修建管道最短?
问题2:新修的两条管道长度有什么关系,画来看看.
O
B
A
C
?
∠AOB
=2∠AOC
=2∠BOC
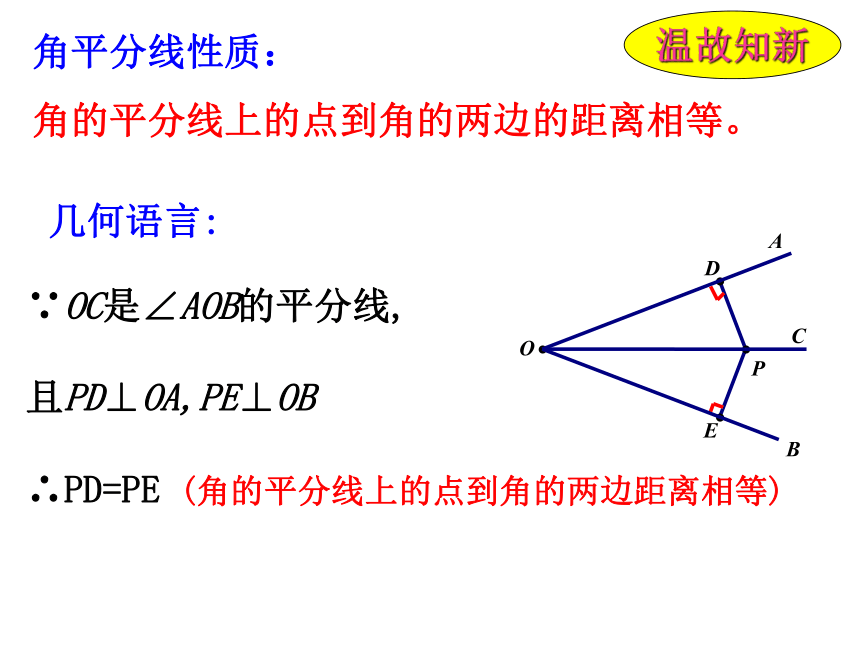
角平分线性质
温故知新
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB
∴PD=PE
(角的平分线上的点到角的两边距离相等)
几何语言:
角平分线性质:
角的平分线上的点到角的两边的距离相等。
E
D
O
A
B
P
C
温故知新
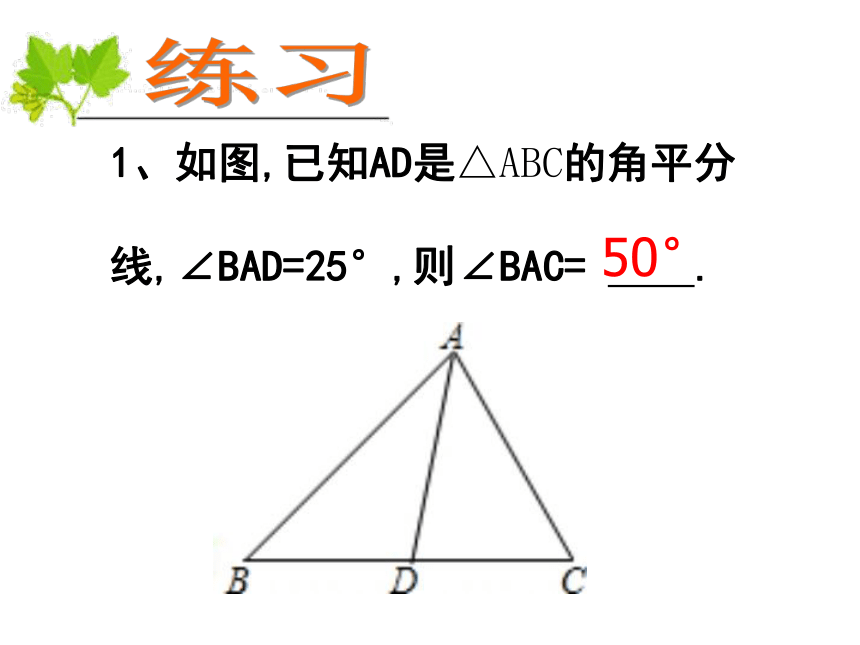
1、如图,已知AD是△ABC的角平分
线,∠BAD=25°,则∠BAC=
.
练习
50°
练习
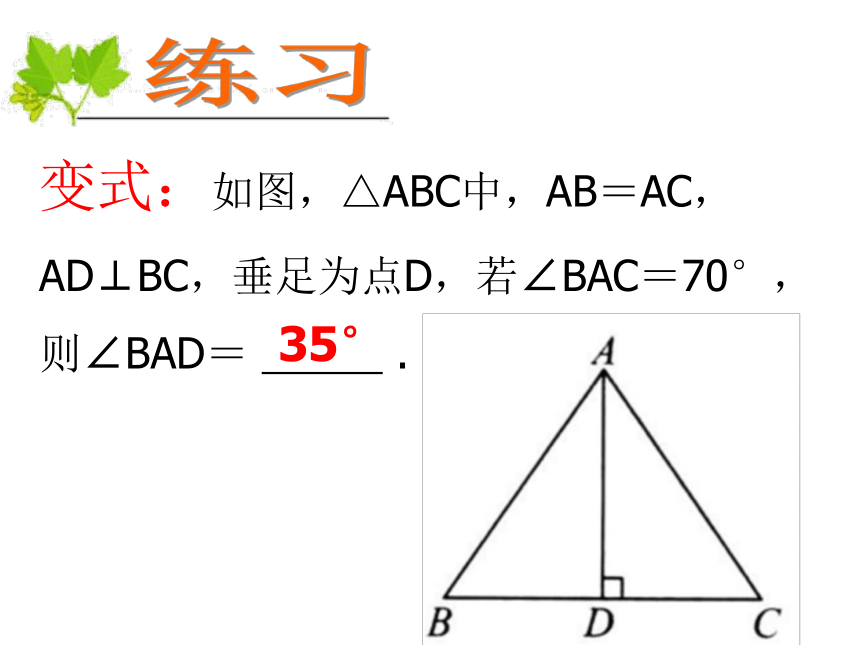
变式:如图,△ABC中,AB=AC,AD⊥BC,垂足为点D,若∠BAC=70°,则∠BAD=
.
35°
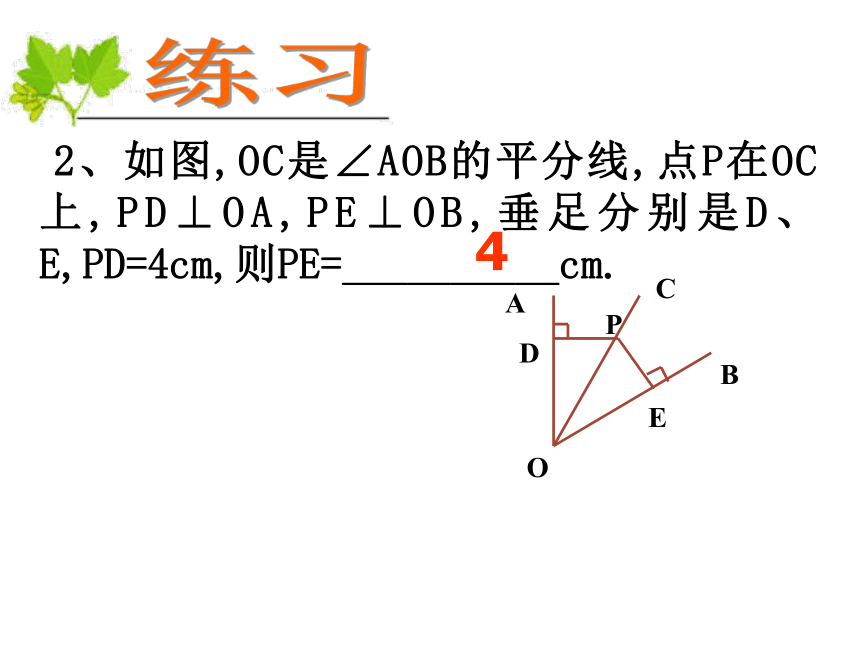
2、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
练习
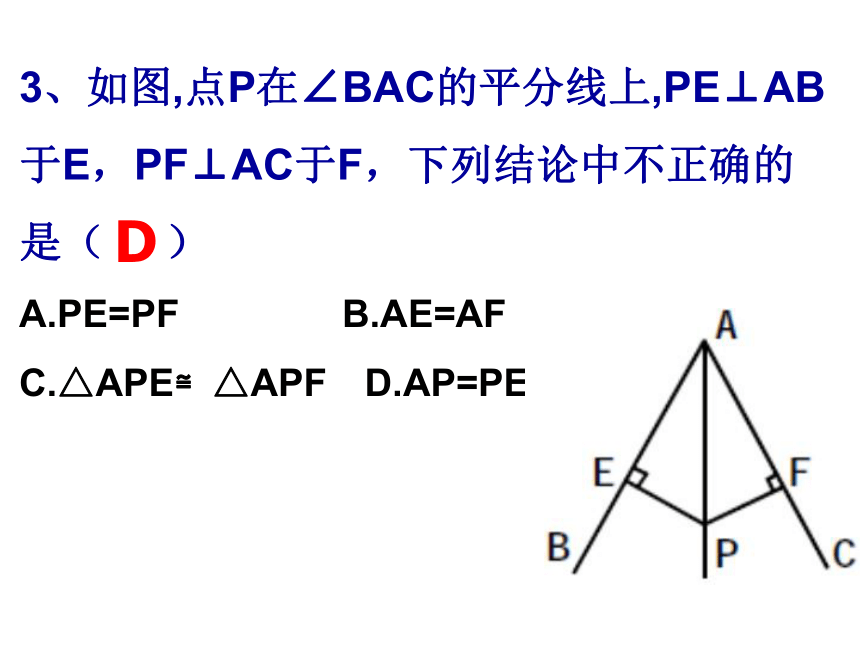
3、如图,点P在∠BAC的平分线上,PE⊥AB
于E,PF⊥AC于F,下列结论中不正确的
是(
)
A.PE=PF
B.AE=AF
C.△APE≌△APF
D.AP=PE
D
4、
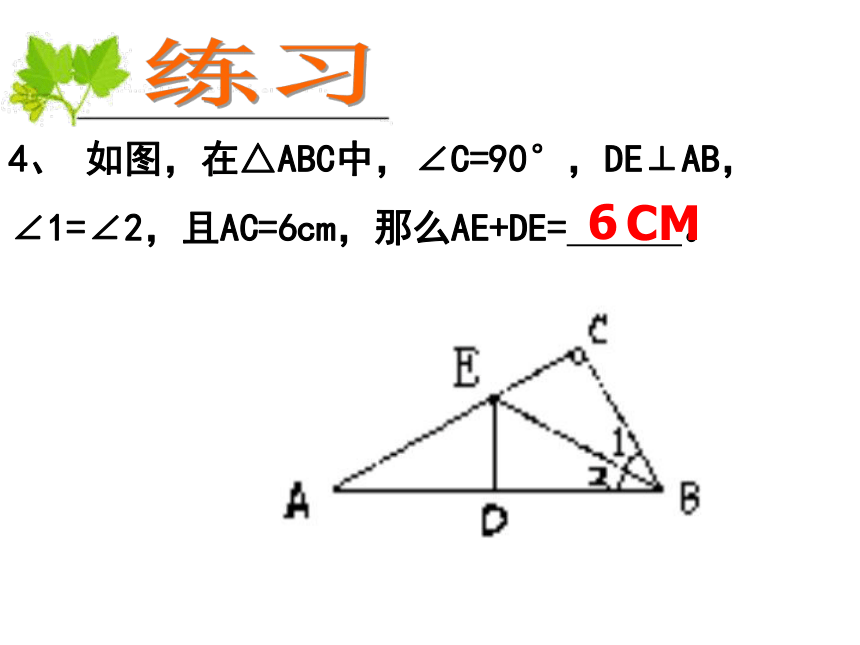
如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么AE+DE= 。
练习
6
CM
变式:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为
。
A
C
D
B
E
练习
E
3
5、如图,已知在△ABC中,CD是AB边上的高线,
BE平分∠ABC,交CD于点E,BC=50,DE=14,则△BCE的面积等于________.
350
练习
变式:如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,S△ABC=7,DE=2,AB=4,则AC长是(
)
A.6
B.5
C.4
D.3
练习
D
6、如图,△ABC中,AD平分∠BAC,且DE⊥AB于E,DF⊥AC于F,若∠ADE=70°,则∠ADF=___.
练习
70°
7、已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
证明:∵ AD平分∠CAB
DE⊥AB,DF⊥AC
∴
DE
=
DF(角平分线的性质)
在Rt△BDE和Rt△CDF中,
DE=DF
(已证)
BD=CD(已知)
∴
Rt△BDE≌Rt△CDF
(HL)
∴
EB=CF
(全等三角形对应边相等)
B
A
E
D
C
F
练习
变式二:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,求证:AB=AC.
B
A
D
C
练习
E
F
8、已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,求证:CF=EB。
证明:
∵ AD平分∠CAB
DE⊥AB,∠C=90°(已知)
∴ CD=DE
(角平分线的性质)
在Rt△CDF和Rt△EDB中,
CD=DE
(已证)
DF=DB
(已知)
∴
Rt△CDF≌Rt△EDB
(HL)
∴
CF=EB
(全等三角形对应边相等)
A
C
D
B
E
F
9、如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC交AC的延长线于点G,求证:BF=CG.
思考
证明:连接BE、EC,
∵ED⊥BC,D为BC中点,
∴BE=EC,
∵EF⊥AB
EG⊥AG,且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
BE=CE,
EF=EG,
∴Rt△BFE≌Rt△CGE
(HL)
∴BF=CG.
提示:连接BE、CE,可先证Rt△BEF≌Rt△CEG
学以致用
一、如图,有三条公路两两相交于A、B、C点处,现计划修建一个加油站,要求到三条公路的距离相等,那么该如何选择加油站的位置?
二、如图,在△ABC中,∠ABC=60?,AD、CE分别平分∠BAC、∠ACB,且AD、CE交于点O.
(1)求∠COD的度数;
(2)求证:OD=OE
P
N
M
O
E
D
A
C
B
下课了!
这节课我们学到了什么?
①利用角平分线性质定理证明两条线段相等.
②灵活运用角平分线的性质解答问题。
小结与作业
O
A
B
N
M
C
角平分线性质的应用
.
P
暖气
天然气
M
N
实际问题
生活中有很多数学问题:
小明家居住在一栋居民楼的一楼,刚好位于一条暖气和天然气管道所成角的平分线上的P点,现要从P点建两条管道,分别与暖气管道和天然气管道相连.
问题1:怎样修建管道最短?
问题2:新修的两条管道长度有什么关系,画来看看.
O
B
A
C
?
∠AOB
=2∠AOC
=2∠BOC
角平分线性质
温故知新
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB
∴PD=PE
(角的平分线上的点到角的两边距离相等)
几何语言:
角平分线性质:
角的平分线上的点到角的两边的距离相等。
E
D
O
A
B
P
C
温故知新
1、如图,已知AD是△ABC的角平分
线,∠BAD=25°,则∠BAC=
.
练习
50°
练习
变式:如图,△ABC中,AB=AC,AD⊥BC,垂足为点D,若∠BAC=70°,则∠BAD=
.
35°
2、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
练习
3、如图,点P在∠BAC的平分线上,PE⊥AB
于E,PF⊥AC于F,下列结论中不正确的
是(
)
A.PE=PF
B.AE=AF
C.△APE≌△APF
D.AP=PE
D
4、
如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么AE+DE= 。
练习
6
CM
变式:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为
。
A
C
D
B
E
练习
E
3
5、如图,已知在△ABC中,CD是AB边上的高线,
BE平分∠ABC,交CD于点E,BC=50,DE=14,则△BCE的面积等于________.
350
练习
变式:如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,S△ABC=7,DE=2,AB=4,则AC长是(
)
A.6
B.5
C.4
D.3
练习
D
6、如图,△ABC中,AD平分∠BAC,且DE⊥AB于E,DF⊥AC于F,若∠ADE=70°,则∠ADF=___.
练习
70°
7、已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
证明:∵ AD平分∠CAB
DE⊥AB,DF⊥AC
∴
DE
=
DF(角平分线的性质)
在Rt△BDE和Rt△CDF中,
DE=DF
(已证)
BD=CD(已知)
∴
Rt△BDE≌Rt△CDF
(HL)
∴
EB=CF
(全等三角形对应边相等)
B
A
E
D
C
F
练习
变式二:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,求证:AB=AC.
B
A
D
C
练习
E
F
8、已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,求证:CF=EB。
证明:
∵ AD平分∠CAB
DE⊥AB,∠C=90°(已知)
∴ CD=DE
(角平分线的性质)
在Rt△CDF和Rt△EDB中,
CD=DE
(已证)
DF=DB
(已知)
∴
Rt△CDF≌Rt△EDB
(HL)
∴
CF=EB
(全等三角形对应边相等)
A
C
D
B
E
F
9、如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC交AC的延长线于点G,求证:BF=CG.
思考
证明:连接BE、EC,
∵ED⊥BC,D为BC中点,
∴BE=EC,
∵EF⊥AB
EG⊥AG,且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
BE=CE,
EF=EG,
∴Rt△BFE≌Rt△CGE
(HL)
∴BF=CG.
提示:连接BE、CE,可先证Rt△BEF≌Rt△CEG
学以致用
一、如图,有三条公路两两相交于A、B、C点处,现计划修建一个加油站,要求到三条公路的距离相等,那么该如何选择加油站的位置?
二、如图,在△ABC中,∠ABC=60?,AD、CE分别平分∠BAC、∠ACB,且AD、CE交于点O.
(1)求∠COD的度数;
(2)求证:OD=OE
P
N
M
O
E
D
A
C
B
下课了!
这节课我们学到了什么?
①利用角平分线性质定理证明两条线段相等.
②灵活运用角平分线的性质解答问题。
小结与作业
