1.1相似多边形-青岛版九年级数学上册课件(共20张PPT)
文档属性
| 名称 | 1.1相似多边形-青岛版九年级数学上册课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 506.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 11:47:06 | ||
图片预览







文档简介
(共20张PPT)
§1.1
相似多边形
第1章
图形的相似
知识回顾
一、什么叫做全等形?
能够完全重合的两个平面图形叫全等形。
二、怎样理解“完全重合”?
完全重合:即形状相同、大小相等。
三、三角形全等的判定方法:
(1)ASA;(2)AAS;(3)SAS;(4)SSS。
四、三角形全等的性质:
1、全等三角形的对应角相等;
2、全等三角形的对应边相等。
在全等多边形中重点学习的全等三角形
上述图形是全等形吗?
2022年北京冬残奥会吉祥物
1、什么叫做相似形?
形状相同的两个平面图形叫相似形。
2、相似形与全等形的关系:
全等形一定是相似形,但相似形不一定
是全等形;即全等形是特殊的相似形。
E
B
D
C
A
D
C
E
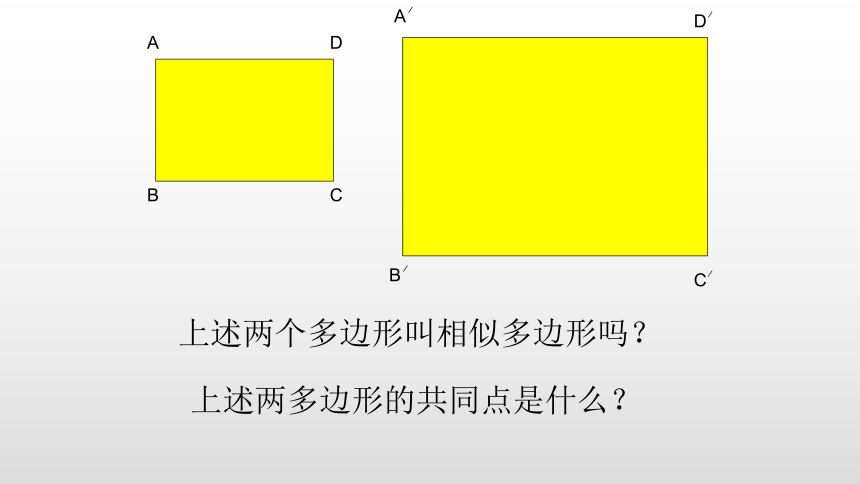
B
A
B
D
C
A
A
B
C
D
上述两个多边形叫相似多边形吗?
上述两多边形的共同点是什么?
3、什么叫做相似多边形?
如果两个多边形的边数相同,并且各角对
应相等,各边对应成比例,那么这两个多
边形叫做相似多边形。
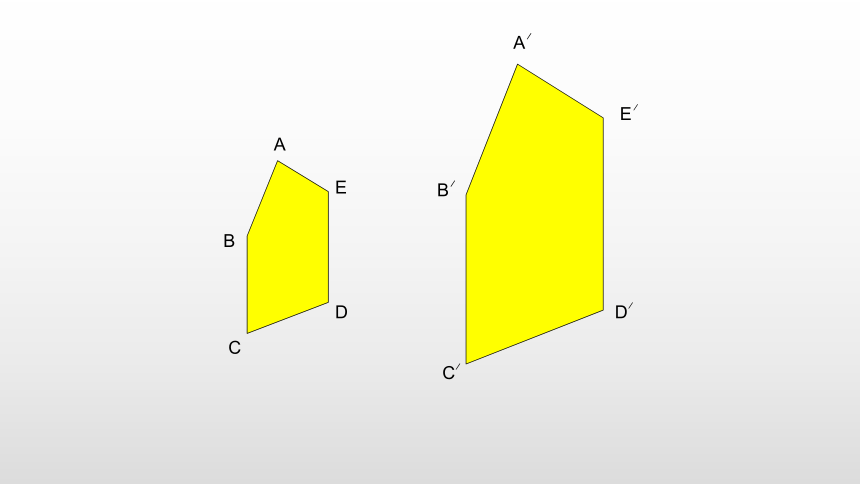
E
B
D
C
A
E′
B′
D′
C′
A′
①相似形的表示方法:
例如:
四边形ABCD与四边形A′B′C′D′相似
记作:
四边形ABCD∽四边形A′B′C′D′
5、相似比的定义:
相似多边形对应边的比叫做相似比。
1、下列各组图中,相似的是(
)
①正六边形和一般六边形
②两个正方形
60°
60°
③两个菱形
┏
2
4
3
┏
1
2
1.5
④直角梯形
A.①②③
B
.②③④
C.
①③④
D.
①②④
2、下列说法中,正确的个数是(
)
①所有的正三角形都相似;②所有的正方形都相似;
③所有的等腰直角三角形都相似;
④所有的矩形都相似;⑤所有的菱形都相似。
A.2个
B.3个
C.4个
D.5个
练习
C
B
A
B
C
E
D
3、已知:如图,△ADE∽
△ABC,说出图中的
对应顶点、对应角和对应边。
练习
对应点:点A与点A,点D与点B,点E与点C
对应角:∠A与∠A,∠ADE与∠B,∠AED与∠C
对应边:AD与AB,AE与AC,DE与BC
6、两多边形相似的判定方法:
若两多边形
①边数相同;
②各角对应相等;
③各边对应成比例,
那么这两多边形相似。
怎样判断多边形相似呢?
例
题
解
析
例1、如图,一个矩形广场的长为60m,宽为40m,广场内四周有两条纵向小路和两条横向小路的宽均为2m。
问:小路内外边缘所围成的两个矩形是否相似?
①相似多边形的对应角相等;
②相似多边形的对应边成比例。
7、相似多边形的性质:
例
题
解
析
例2、如图,已知四边形ABCD∽四边形A′B′C′D′,
AD=18,CD=21,A′D′=24,∠A=65°,∠B=85°,∠C=60°.
求:(1)∠A′,∠B′,∠C′与∠D′的度数;
(2)C′D′的长度。
A
D
C
B
A′
D′
C′
B′
(1)∵四边形ABCD∽四边形A′B′C′D′,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′
∵∠A=65°,∠B=85°,∠C=60°
∴∠A′=65°,∠B′=85°,∠C′=60°
∴∠D′=150°
(2)∵四边形ABCD∽四边形A′B′C′D′,
∴
∵AD=18,CD=21,A′D′=24,
∴
∴
C′D′=28
例2、两个相似五边形中,一个各边长分别为
1,2,3,4,5,另一个最大边长为10,则后一
个五边形的最小边为_____.
例3、如图,将矩形ABCD对折,折痕为MN,若
矩形ABNM与矩形
ABCD相似.
求:矩形ABNM与矩形ABCD相似比。
B
D
C
A
M
N
2
通过这节课的学习你有什么收获?
相似多边形的有关概念及性质
作
业
52页A组1,2题.
53页B组1题。
不经历风雨,怎么见彩虹
没有人能随随便便成功!
再见
§1.1
相似多边形
第1章
图形的相似
知识回顾
一、什么叫做全等形?
能够完全重合的两个平面图形叫全等形。
二、怎样理解“完全重合”?
完全重合:即形状相同、大小相等。
三、三角形全等的判定方法:
(1)ASA;(2)AAS;(3)SAS;(4)SSS。
四、三角形全等的性质:
1、全等三角形的对应角相等;
2、全等三角形的对应边相等。
在全等多边形中重点学习的全等三角形
上述图形是全等形吗?
2022年北京冬残奥会吉祥物
1、什么叫做相似形?
形状相同的两个平面图形叫相似形。
2、相似形与全等形的关系:
全等形一定是相似形,但相似形不一定
是全等形;即全等形是特殊的相似形。
E
B
D
C
A
D
C
E
B
A
B
D
C
A
A
B
C
D
上述两个多边形叫相似多边形吗?
上述两多边形的共同点是什么?
3、什么叫做相似多边形?
如果两个多边形的边数相同,并且各角对
应相等,各边对应成比例,那么这两个多
边形叫做相似多边形。
E
B
D
C
A
E′
B′
D′
C′
A′
①相似形的表示方法:
例如:
四边形ABCD与四边形A′B′C′D′相似
记作:
四边形ABCD∽四边形A′B′C′D′
5、相似比的定义:
相似多边形对应边的比叫做相似比。
1、下列各组图中,相似的是(
)
①正六边形和一般六边形
②两个正方形
60°
60°
③两个菱形
┏
2
4
3
┏
1
2
1.5
④直角梯形
A.①②③
B
.②③④
C.
①③④
D.
①②④
2、下列说法中,正确的个数是(
)
①所有的正三角形都相似;②所有的正方形都相似;
③所有的等腰直角三角形都相似;
④所有的矩形都相似;⑤所有的菱形都相似。
A.2个
B.3个
C.4个
D.5个
练习
C
B
A
B
C
E
D
3、已知:如图,△ADE∽
△ABC,说出图中的
对应顶点、对应角和对应边。
练习
对应点:点A与点A,点D与点B,点E与点C
对应角:∠A与∠A,∠ADE与∠B,∠AED与∠C
对应边:AD与AB,AE与AC,DE与BC
6、两多边形相似的判定方法:
若两多边形
①边数相同;
②各角对应相等;
③各边对应成比例,
那么这两多边形相似。
怎样判断多边形相似呢?
例
题
解
析
例1、如图,一个矩形广场的长为60m,宽为40m,广场内四周有两条纵向小路和两条横向小路的宽均为2m。
问:小路内外边缘所围成的两个矩形是否相似?
①相似多边形的对应角相等;
②相似多边形的对应边成比例。
7、相似多边形的性质:
例
题
解
析
例2、如图,已知四边形ABCD∽四边形A′B′C′D′,
AD=18,CD=21,A′D′=24,∠A=65°,∠B=85°,∠C=60°.
求:(1)∠A′,∠B′,∠C′与∠D′的度数;
(2)C′D′的长度。
A
D
C
B
A′
D′
C′
B′
(1)∵四边形ABCD∽四边形A′B′C′D′,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′
∵∠A=65°,∠B=85°,∠C=60°
∴∠A′=65°,∠B′=85°,∠C′=60°
∴∠D′=150°
(2)∵四边形ABCD∽四边形A′B′C′D′,
∴
∵AD=18,CD=21,A′D′=24,
∴
∴
C′D′=28
例2、两个相似五边形中,一个各边长分别为
1,2,3,4,5,另一个最大边长为10,则后一
个五边形的最小边为_____.
例3、如图,将矩形ABCD对折,折痕为MN,若
矩形ABNM与矩形
ABCD相似.
求:矩形ABNM与矩形ABCD相似比。
B
D
C
A
M
N
2
通过这节课的学习你有什么收获?
相似多边形的有关概念及性质
作
业
52页A组1,2题.
53页B组1题。
不经历风雨,怎么见彩虹
没有人能随随便便成功!
再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
