1.2.2数轴-人教版七年级数学上册课件(共16张PPT)
文档属性
| 名称 | 1.2.2数轴-人教版七年级数学上册课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 668.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 11:48:49 | ||
图片预览




文档简介
(共16张PPT)
-4
-3
-2
-1
0
1
2
3
4
正方向
原点
单位长度
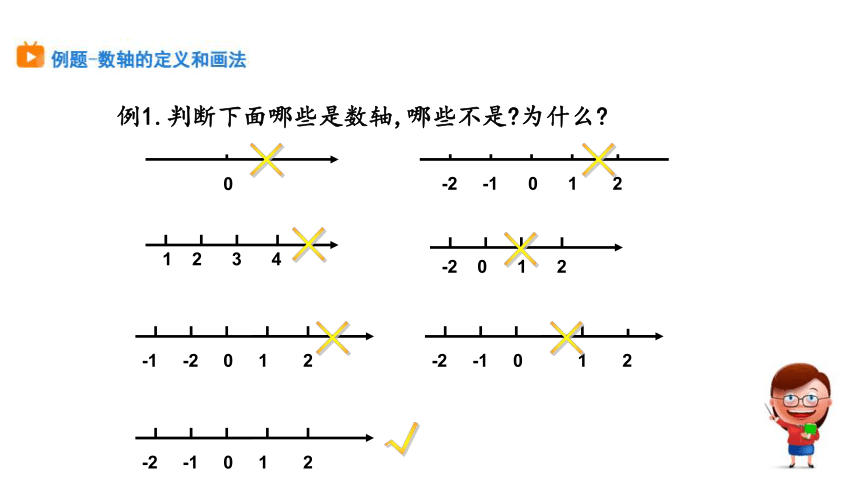
1.数轴定义:规定了原点、正方向、单位长度的直线
数轴
情境导入
小红、小蓝、小花三人从同一地点出发,去往同一条直线上不同的地方,怎么用数学知识表示他们的具体位置呢?
解释:
1.在直线上取一点O表示0,这个点叫做原点
2.通常规定从原点向右(或上为正方向)
3.单位长度:可根据实际情况灵活选用
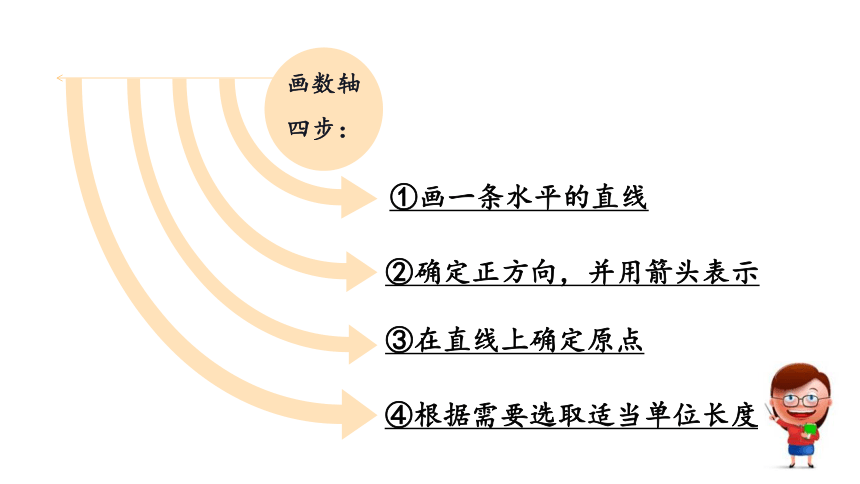
例1.判断下面哪些是数轴,哪些不是?为什么?
0
-2
-1
0
1
2
1
2
3
4
-2
0
1
2
-1
-2
0
1
2
-2
-1
0
1
2
-2
-1
0
1
2
×
×
×
×
×
×
√
单位长度固定么?
-40
-30
-20
-10
0
10
20
30
40
-20
-15
-10
-5
0
5
10
15
20
单位长度根据实际情况确定
数轴上只能标注有理数么?
NO!!
所有有理数和无理数都可以标注
画数轴
四步:
①画一条水平的直线
②确定正方向,并用箭头表示
③在直线上确定原点
④根据需要选取适当单位长度
-4
-3
-2
-1
0
1
2
3
4
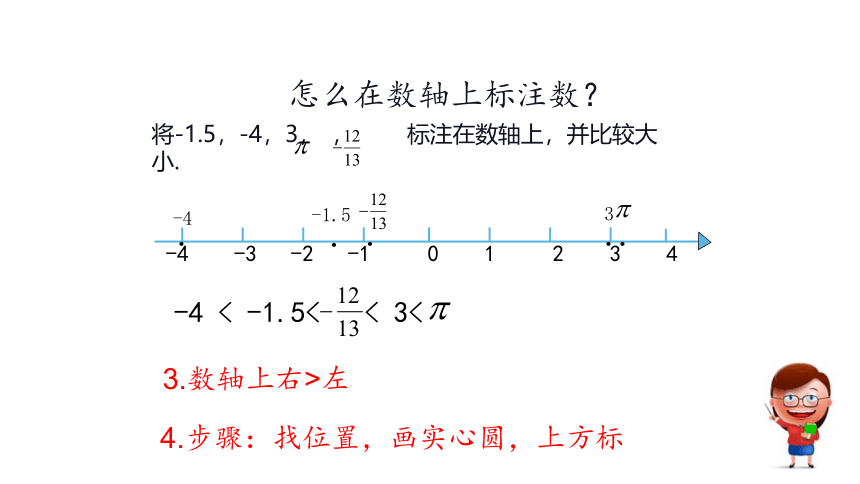
4.步骤:找位置,画实心圆,上方标
-4
<
-1.5<
<
3<
-1.5
怎么在数轴上标注数?
将-1.5,-4,3,
,
标注在数轴上,并比较大小.
.
-4
.
3
.
.
.
3.数轴上右>左
问题1:两点间距离怎么求?
(如:-3与5的距离)
两点间距离:数格法、计算法(右-左)
-5
-4
-3
-2
-1
0
1
2
3
4
5
一起解决
问题2:平移后的点怎么求?
(如:由-2向右平移5各单位长度)
平移后的点:数格法、计算法(右+左-)
-5
-4
-3
-2
-1
0
1
2
3
4
5
一起解决
问题3:求到某点的距离有几个?怎么求?
(如:求到2的距离为5的点)
到某点距离:左右数格法、左右计算法(右+左-)
-5
-4
-3
-2
-1
0
1
2
3
4
5
一起解决
例题1.数轴上一点P表示的数是6,先把这个点向右移动3个单位长度,再向左移动5个单位长度,则点P表示的数是
.
例题2.数轴上到-4的距离是2的数是
.
6+3-5=4
-4+2=-2
-4-2=-6
例题3.数轴上表示整数的点叫做整点,某数轴的单位长度是1cm,若在数轴上任意画一条长度为3cm的线段AB,线段AB能盖住的整点数有
个.
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
在数轴上任意画一条ncm的线段,盖住的整点数是n或n+1个
提升练习
提升1.如图,在数轴上,点A、B分别在原点O的两侧,且到原点的距离均为2个单位长度,若点A以每秒3个单位长度,点B以每秒1个单位长度的速度均向右运动,当点A与点B重合时,他们对应的数为
.
-4
-3
-2
-1
0
1
2
3
4
A
B
设运动时间为t秒
-4
-3
-2
-1
0
1
2
3
4
A
B
方法一:
追及问题/对面相遇问题
追及路程=速度差×追及时间
4=(3-1)×t
t=2
2+1×2=4
-4
-3
-2
-1
0
1
2
3
4
A
B
方法二:
表示运动点在数轴上对应的数
t秒后点A对应的数:-2+3t
t秒后点B对应的数:2+t
当点A与B重合时,点A对应的数与点B对应的数相等
-2+3t=2+t
t=2
2+t=2+2=4
总结
表示点A运动后点对应的数:
点A+速度×时间(向右运动)
点A-速度×时间(向左运动)
-4
-3
-2
-1
0
1
2
3
4
正方向
原点
单位长度
1.数轴定义:规定了原点、正方向、单位长度的直线
数轴
情境导入
小红、小蓝、小花三人从同一地点出发,去往同一条直线上不同的地方,怎么用数学知识表示他们的具体位置呢?
解释:
1.在直线上取一点O表示0,这个点叫做原点
2.通常规定从原点向右(或上为正方向)
3.单位长度:可根据实际情况灵活选用
例1.判断下面哪些是数轴,哪些不是?为什么?
0
-2
-1
0
1
2
1
2
3
4
-2
0
1
2
-1
-2
0
1
2
-2
-1
0
1
2
-2
-1
0
1
2
×
×
×
×
×
×
√
单位长度固定么?
-40
-30
-20
-10
0
10
20
30
40
-20
-15
-10
-5
0
5
10
15
20
单位长度根据实际情况确定
数轴上只能标注有理数么?
NO!!
所有有理数和无理数都可以标注
画数轴
四步:
①画一条水平的直线
②确定正方向,并用箭头表示
③在直线上确定原点
④根据需要选取适当单位长度
-4
-3
-2
-1
0
1
2
3
4
4.步骤:找位置,画实心圆,上方标
-4
<
-1.5<
<
3<
-1.5
怎么在数轴上标注数?
将-1.5,-4,3,
,
标注在数轴上,并比较大小.
.
-4
.
3
.
.
.
3.数轴上右>左
问题1:两点间距离怎么求?
(如:-3与5的距离)
两点间距离:数格法、计算法(右-左)
-5
-4
-3
-2
-1
0
1
2
3
4
5
一起解决
问题2:平移后的点怎么求?
(如:由-2向右平移5各单位长度)
平移后的点:数格法、计算法(右+左-)
-5
-4
-3
-2
-1
0
1
2
3
4
5
一起解决
问题3:求到某点的距离有几个?怎么求?
(如:求到2的距离为5的点)
到某点距离:左右数格法、左右计算法(右+左-)
-5
-4
-3
-2
-1
0
1
2
3
4
5
一起解决
例题1.数轴上一点P表示的数是6,先把这个点向右移动3个单位长度,再向左移动5个单位长度,则点P表示的数是
.
例题2.数轴上到-4的距离是2的数是
.
6+3-5=4
-4+2=-2
-4-2=-6
例题3.数轴上表示整数的点叫做整点,某数轴的单位长度是1cm,若在数轴上任意画一条长度为3cm的线段AB,线段AB能盖住的整点数有
个.
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
在数轴上任意画一条ncm的线段,盖住的整点数是n或n+1个
提升练习
提升1.如图,在数轴上,点A、B分别在原点O的两侧,且到原点的距离均为2个单位长度,若点A以每秒3个单位长度,点B以每秒1个单位长度的速度均向右运动,当点A与点B重合时,他们对应的数为
.
-4
-3
-2
-1
0
1
2
3
4
A
B
设运动时间为t秒
-4
-3
-2
-1
0
1
2
3
4
A
B
方法一:
追及问题/对面相遇问题
追及路程=速度差×追及时间
4=(3-1)×t
t=2
2+1×2=4
-4
-3
-2
-1
0
1
2
3
4
A
B
方法二:
表示运动点在数轴上对应的数
t秒后点A对应的数:-2+3t
t秒后点B对应的数:2+t
当点A与B重合时,点A对应的数与点B对应的数相等
-2+3t=2+t
t=2
2+t=2+2=4
总结
表示点A运动后点对应的数:
点A+速度×时间(向右运动)
点A-速度×时间(向左运动)
