2020-2021 学年人教版 八年级数学上册 12.2 全等三角形的判定 课后训练(Word版 含答案)
文档属性
| 名称 | 2020-2021 学年人教版 八年级数学上册 12.2 全等三角形的判定 课后训练(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-04 00:00:00 | ||
图片预览

文档简介
2020-2021
人教版
八年级数学上册
12.2
全等三角形的判定
课后训练(含答案)
一、选择题(本大题共8道小题)
1.
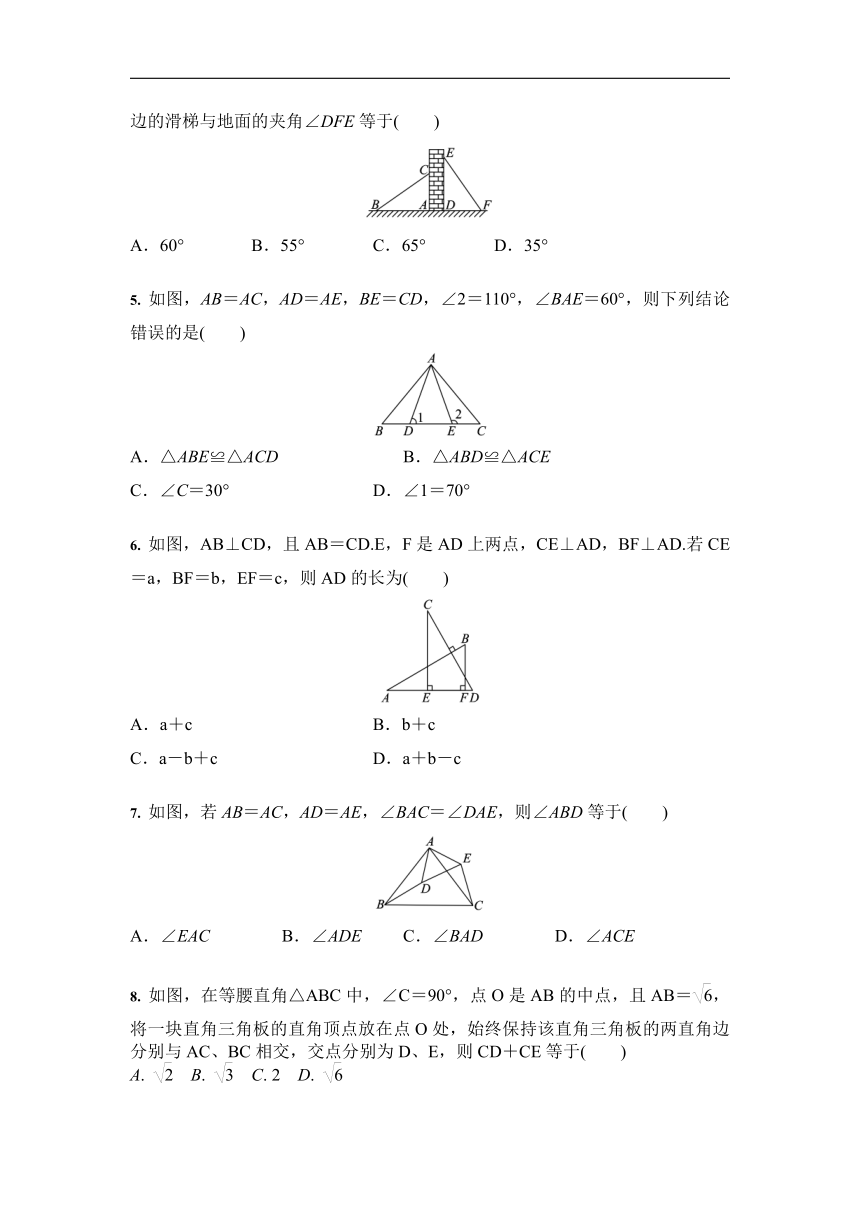
如图,AD=AE,若利用“SAS”证明△ABE≌△ACD,则需要添加的条件是( )
A.AB=AC
B.∠B=∠C
C.∠AEB=∠ADC
D.∠A=∠B
2.
如图所示,P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
A.HL
B.ASA
C.AAS
D.SAS
3.
如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=DB
D.AB=DC
4.
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE等于( )
A.60°
B.55°
C.65°
D.35°
5.
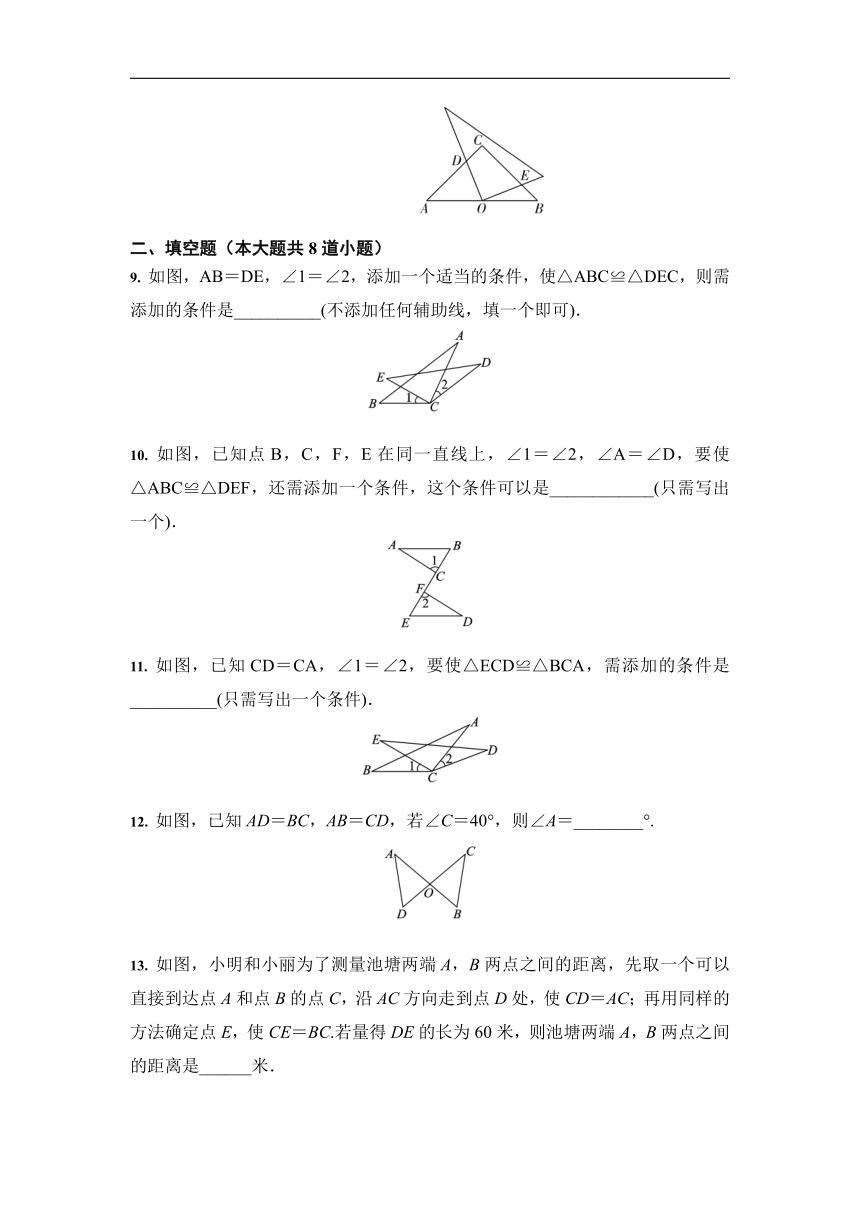
如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠C=30°
D.∠1=70°
6.
如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c
B.b+c
C.a-b+c
D.a+b-c
7.
如图,若AB=AC,AD=AE,∠BAC=∠DAE,则∠ABD等于( )
A.∠EAC
B.∠ADE
C.∠BAD
D.∠ACE
8.
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE等于( )
A.
B.
C.
2
D.
二、填空题(本大题共8道小题)
9.
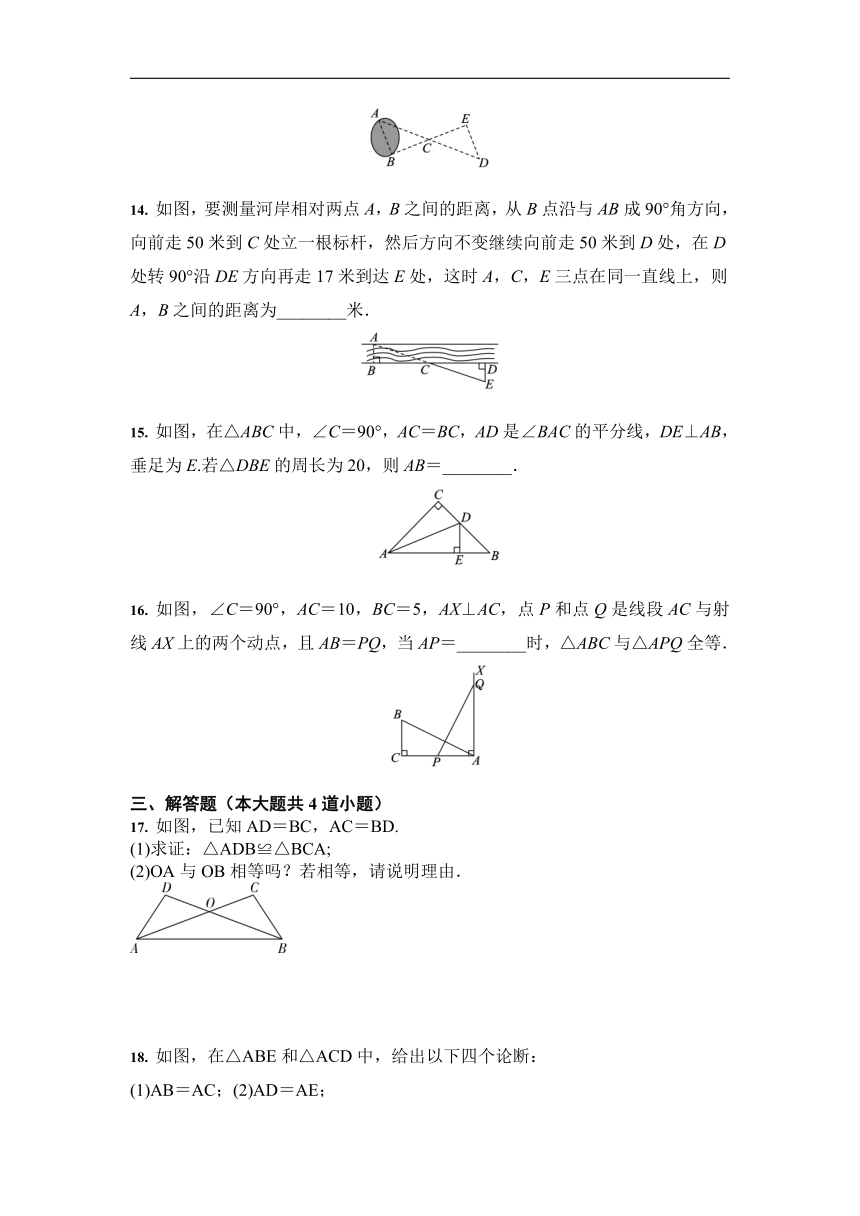
如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
10.
如图,已知点B,C,F,E在同一直线上,∠1=∠2,∠A=∠D,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是____________(只需写出一个).
11.
如图,已知CD=CA,∠1=∠2,要使△ECD≌△BCA,需添加的条件是__________(只需写出一个条件).
12.
如图,已知AD=BC,AB=CD,若∠C=40°,则∠A=________°.
13.
如图,小明和小丽为了测量池塘两端A,B两点之间的距离,先取一个可以直接到达点A和点B的点C,沿AC方向走到点D处,使CD=AC;再用同样的方法确定点E,使CE=BC.若量得DE的长为60米,则池塘两端A,B两点之间的距离是______米.
14.
如图,要测量河岸相对两点A,B之间的距离,从B点沿与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续向前走50米到D处,在D处转90°沿DE方向再走17米到达E处,这时A,C,E三点在同一直线上,则A,B之间的距离为________米.
15.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.
16.
如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
三、解答题(本大题共4道小题)
17.
如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA;
(2)OA与OB相等吗?若相等,请说明理由.
18.
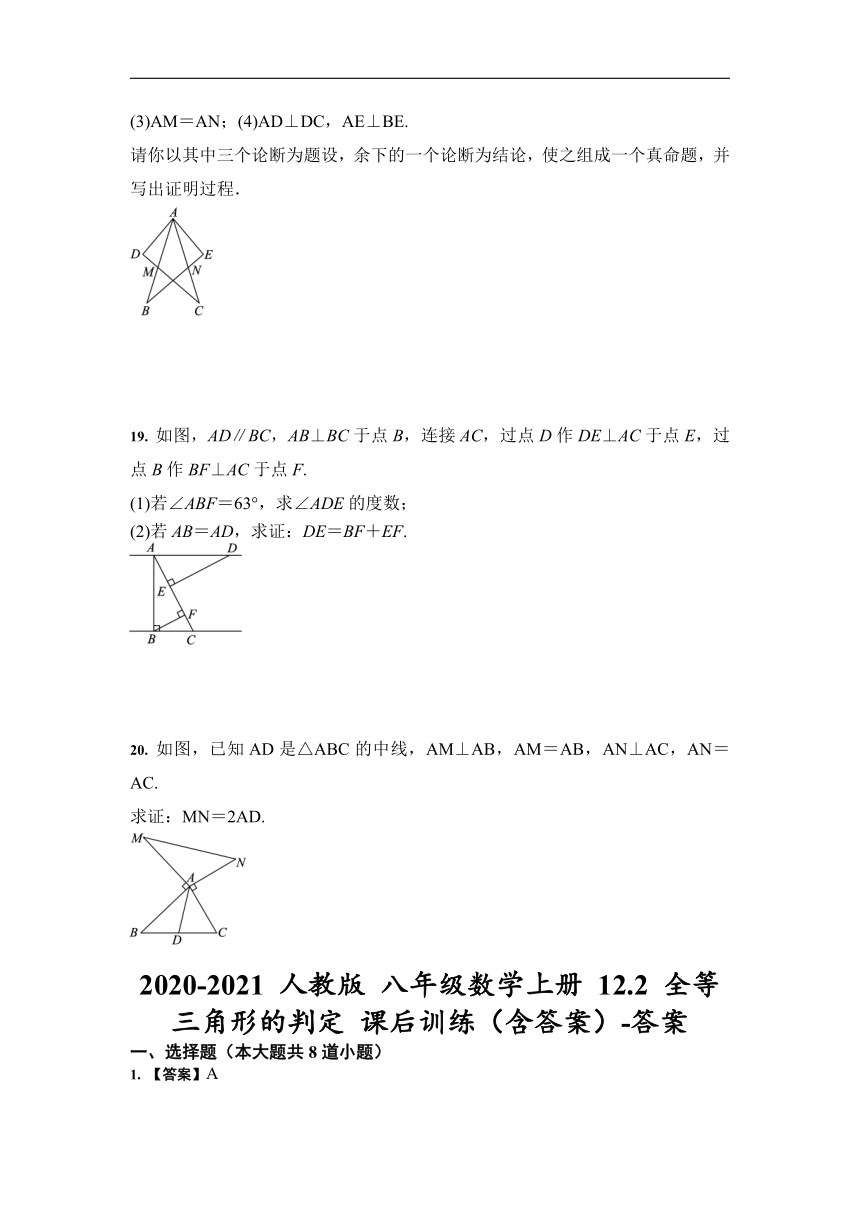
如图,在△ABE和△ACD中,给出以下四个论断:
(1)AB=AC;(2)AD=AE;
(3)AM=AN;(4)AD⊥DC,AE⊥BE.
请你以其中三个论断为题设,余下的一个论断为结论,使之组成一个真命题,并写出证明过程.
19.
如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)若AB=AD,求证:DE=BF+EF.
20.
如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.
求证:MN=2AD.
2020-2021
人教版
八年级数学上册
12.2
全等三角形的判定
课后训练(含答案)-答案
一、选择题(本大题共8道小题)
1.
【答案】A
2.
【答案】A
3.
【答案】C [解析]
A.∠A=∠D,∠ABC=∠DCB,BC=BC,符合“AAS”,即能推出△ABC≌△DCB,故本选项不符合题意;
B.∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合“ASA”,即能推出△ABC≌△DCB,故本选项不符合题意;
C.∠ABC=∠DCB,AC=DB,BC=BC,不符合全等三角形的判定条件,即不能推出△ABC≌△DCB,故本选项符合题意;
D.AB=DC,∠ABC=∠DCB,BC=CB,符合“SAS”,即能推出△ABC≌△DCB,故本选项不符合题意.
故选C.
4.
【答案】B [解析]
在Rt△ABC和Rt△DEF中,∴Rt△ABC≌Rt△DEF(HL).
∴∠DEF=∠ABC=35°.
∴∠DFE=90°-35°=55°.
5.
【答案】C [解析]
∵BE=CD,
∴BE-DE=CD-DE,即BD=CE.
在△ABD和△ACE中,
∴△ABD≌△ACE.
由题意易证:△ABE≌△ACD,故A,B正确.
由△ABE≌△ACD可得∠B=∠C.
∵∠2=∠BAE+∠B,
∴∠B=∠2-∠BAE=110°-60°=50°.
∴∠C=∠B=50°.
故C错误.
∵△ABE≌△ACD(已证),∴∠1=∠AED=180°-∠2=70°.
故D正确.故选C.
6.
【答案】D [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠CED=∠AFB=90°,∠A=∠C.又∵AB=CD,∴△CED≌△AFB.∴AF=CE=a,DE=BF=b,DF=DE-EF=b-c.∴AD=AF+DF=a+b-c.故选D.
7.
【答案】D [解析]
∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
8.
【答案】B 【解析】如解图,连接OC,由已知条件易得∠A=∠OCE,CO=AO,∠DOE=∠COA,∴∠DOE-∠COD=∠COA-∠COD,即∠AOD=∠COE,∴△AOD≌△COE(ASA),∴AD=CE,进而得CD+CE=CD+AD=AC=AB=,故选B.
二、填空题(本大题共8道小题)
9.
【答案】答案不唯一,如∠B=∠E
10.
【答案】AB=DE(答案不唯一)
11.
【答案】答案不唯一,如CE=CB [解析]
由∠1=∠2,可得∠DCE=∠ACB,又∵CD=CA,∴添加CE=CB,可根据“SAS”判定两个三角形全等.
12.
【答案】40 [解析]
如图,连接DB.
在△ADB和△CBD中,
∴△ADB≌△CBD(SSS).
∴∠A=∠C=40°.
13.
【答案】60 [解析]
在△ACB和△DCE中,
∴△ACB≌△DCE(SAS).∴DE=AB.
∵DE=60米,∴AB=60米.
14.
【答案】17 [解析]
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA).
∴AB=ED=17米.
15.
【答案】20 [解析]
由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB=AE+EB=AB.
16.
【答案】5或10 [解析]
∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
三、解答题(本大题共4道小题)
17.
【答案】
(1)证明:在△ADB和△BCA中,
,
∴△ADB≌△BCA(SSS).(4分)
(2)解:相等.理由如下:
由(1)得△ADB≌△BCA,
∴∠DBA
=∠CAB,即∠OBA
=∠OAB,(6分)
∴OA=OB.(8分)
18.
【答案】
解:若要组成真命题,则论断(4)必须作为条件.因此可组成以下三个真命题:
命题①:若(1)(2)(4),则(3);命题②:若(1)(3)(4),则(2);命题③:若(2)(3)(4),则(1).
下面以命题①为例进行证明:
∵AD⊥DC,AE⊥BE,∴∠D=∠E=90°.
在Rt△ABE和Rt△ACD中,
∴Rt△ABE≌Rt△ACD(HL).
∴∠BAE=∠CAD.
∴∠BAE-∠BAC=∠CAD-∠BAC,
即∠EAN=∠DAM.
在△ADM和△AEN中,
∴△ADM≌△AEN(ASA).
∴AM=AN.
19.
【答案】
解:(1)∵AD∥BC,AB⊥BC,
∴∠ABC=∠BAD=90°.
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
∴∠ABF+∠BAF=∠BAF+∠DAE=90°.
∴∠DAE=∠ABF=63°.∴∠ADE=27°.
(2)证明:由(1)得∠DAE=∠ABF,∠AED=∠BFA=90°.
在△DAE和△ABF中,
∴△DAE≌△ABF(AAS).
∴AE=BF,DE=AF.
∴DE=AF=AE+EF=BF+EF.
20.
【答案】
证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的中线,
∴BD=CD.
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS).
∴BE=AC=AN,∠DBE=∠DCA.
∴AC∥BE.∴∠ABE+∠BAC=180°.
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°.
∴∠ABE=∠MAN.
在△ABE和△MAN中,
∴△ABE≌△MAN(SAS).
∴AE=MN.
∵AE=2AD,∴MN=2AD.
人教版
八年级数学上册
12.2
全等三角形的判定
课后训练(含答案)
一、选择题(本大题共8道小题)
1.
如图,AD=AE,若利用“SAS”证明△ABE≌△ACD,则需要添加的条件是( )
A.AB=AC
B.∠B=∠C
C.∠AEB=∠ADC
D.∠A=∠B
2.
如图所示,P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
A.HL
B.ASA
C.AAS
D.SAS
3.
如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=DB
D.AB=DC
4.
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE等于( )
A.60°
B.55°
C.65°
D.35°
5.
如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠C=30°
D.∠1=70°
6.
如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c
B.b+c
C.a-b+c
D.a+b-c
7.
如图,若AB=AC,AD=AE,∠BAC=∠DAE,则∠ABD等于( )
A.∠EAC
B.∠ADE
C.∠BAD
D.∠ACE
8.
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE等于( )
A.
B.
C.
2
D.
二、填空题(本大题共8道小题)
9.
如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
10.
如图,已知点B,C,F,E在同一直线上,∠1=∠2,∠A=∠D,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是____________(只需写出一个).
11.
如图,已知CD=CA,∠1=∠2,要使△ECD≌△BCA,需添加的条件是__________(只需写出一个条件).
12.
如图,已知AD=BC,AB=CD,若∠C=40°,则∠A=________°.
13.
如图,小明和小丽为了测量池塘两端A,B两点之间的距离,先取一个可以直接到达点A和点B的点C,沿AC方向走到点D处,使CD=AC;再用同样的方法确定点E,使CE=BC.若量得DE的长为60米,则池塘两端A,B两点之间的距离是______米.
14.
如图,要测量河岸相对两点A,B之间的距离,从B点沿与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续向前走50米到D处,在D处转90°沿DE方向再走17米到达E处,这时A,C,E三点在同一直线上,则A,B之间的距离为________米.
15.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.
16.
如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
三、解答题(本大题共4道小题)
17.
如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA;
(2)OA与OB相等吗?若相等,请说明理由.
18.
如图,在△ABE和△ACD中,给出以下四个论断:
(1)AB=AC;(2)AD=AE;
(3)AM=AN;(4)AD⊥DC,AE⊥BE.
请你以其中三个论断为题设,余下的一个论断为结论,使之组成一个真命题,并写出证明过程.
19.
如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)若AB=AD,求证:DE=BF+EF.
20.
如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.
求证:MN=2AD.
2020-2021
人教版
八年级数学上册
12.2
全等三角形的判定
课后训练(含答案)-答案
一、选择题(本大题共8道小题)
1.
【答案】A
2.
【答案】A
3.
【答案】C [解析]
A.∠A=∠D,∠ABC=∠DCB,BC=BC,符合“AAS”,即能推出△ABC≌△DCB,故本选项不符合题意;
B.∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合“ASA”,即能推出△ABC≌△DCB,故本选项不符合题意;
C.∠ABC=∠DCB,AC=DB,BC=BC,不符合全等三角形的判定条件,即不能推出△ABC≌△DCB,故本选项符合题意;
D.AB=DC,∠ABC=∠DCB,BC=CB,符合“SAS”,即能推出△ABC≌△DCB,故本选项不符合题意.
故选C.
4.
【答案】B [解析]
在Rt△ABC和Rt△DEF中,∴Rt△ABC≌Rt△DEF(HL).
∴∠DEF=∠ABC=35°.
∴∠DFE=90°-35°=55°.
5.
【答案】C [解析]
∵BE=CD,
∴BE-DE=CD-DE,即BD=CE.
在△ABD和△ACE中,
∴△ABD≌△ACE.
由题意易证:△ABE≌△ACD,故A,B正确.
由△ABE≌△ACD可得∠B=∠C.
∵∠2=∠BAE+∠B,
∴∠B=∠2-∠BAE=110°-60°=50°.
∴∠C=∠B=50°.
故C错误.
∵△ABE≌△ACD(已证),∴∠1=∠AED=180°-∠2=70°.
故D正确.故选C.
6.
【答案】D [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠CED=∠AFB=90°,∠A=∠C.又∵AB=CD,∴△CED≌△AFB.∴AF=CE=a,DE=BF=b,DF=DE-EF=b-c.∴AD=AF+DF=a+b-c.故选D.
7.
【答案】D [解析]
∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
8.
【答案】B 【解析】如解图,连接OC,由已知条件易得∠A=∠OCE,CO=AO,∠DOE=∠COA,∴∠DOE-∠COD=∠COA-∠COD,即∠AOD=∠COE,∴△AOD≌△COE(ASA),∴AD=CE,进而得CD+CE=CD+AD=AC=AB=,故选B.
二、填空题(本大题共8道小题)
9.
【答案】答案不唯一,如∠B=∠E
10.
【答案】AB=DE(答案不唯一)
11.
【答案】答案不唯一,如CE=CB [解析]
由∠1=∠2,可得∠DCE=∠ACB,又∵CD=CA,∴添加CE=CB,可根据“SAS”判定两个三角形全等.
12.
【答案】40 [解析]
如图,连接DB.
在△ADB和△CBD中,
∴△ADB≌△CBD(SSS).
∴∠A=∠C=40°.
13.
【答案】60 [解析]
在△ACB和△DCE中,
∴△ACB≌△DCE(SAS).∴DE=AB.
∵DE=60米,∴AB=60米.
14.
【答案】17 [解析]
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA).
∴AB=ED=17米.
15.
【答案】20 [解析]
由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB=AE+EB=AB.
16.
【答案】5或10 [解析]
∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
三、解答题(本大题共4道小题)
17.
【答案】
(1)证明:在△ADB和△BCA中,
,
∴△ADB≌△BCA(SSS).(4分)
(2)解:相等.理由如下:
由(1)得△ADB≌△BCA,
∴∠DBA
=∠CAB,即∠OBA
=∠OAB,(6分)
∴OA=OB.(8分)
18.
【答案】
解:若要组成真命题,则论断(4)必须作为条件.因此可组成以下三个真命题:
命题①:若(1)(2)(4),则(3);命题②:若(1)(3)(4),则(2);命题③:若(2)(3)(4),则(1).
下面以命题①为例进行证明:
∵AD⊥DC,AE⊥BE,∴∠D=∠E=90°.
在Rt△ABE和Rt△ACD中,
∴Rt△ABE≌Rt△ACD(HL).
∴∠BAE=∠CAD.
∴∠BAE-∠BAC=∠CAD-∠BAC,
即∠EAN=∠DAM.
在△ADM和△AEN中,
∴△ADM≌△AEN(ASA).
∴AM=AN.
19.
【答案】
解:(1)∵AD∥BC,AB⊥BC,
∴∠ABC=∠BAD=90°.
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
∴∠ABF+∠BAF=∠BAF+∠DAE=90°.
∴∠DAE=∠ABF=63°.∴∠ADE=27°.
(2)证明:由(1)得∠DAE=∠ABF,∠AED=∠BFA=90°.
在△DAE和△ABF中,
∴△DAE≌△ABF(AAS).
∴AE=BF,DE=AF.
∴DE=AF=AE+EF=BF+EF.
20.
【答案】
证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的中线,
∴BD=CD.
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS).
∴BE=AC=AN,∠DBE=∠DCA.
∴AC∥BE.∴∠ABE+∠BAC=180°.
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°.
∴∠ABE=∠MAN.
在△ABE和△MAN中,
∴△ABE≌△MAN(SAS).
∴AE=MN.
∵AE=2AD,∴MN=2AD.
