16.2最简二次根式和同类二次根式-沪教版(上海)八年级数学上册课件(2课时 共32张PPT)
文档属性
| 名称 | 16.2最简二次根式和同类二次根式-沪教版(上海)八年级数学上册课件(2课时 共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 09:40:58 | ||
图片预览





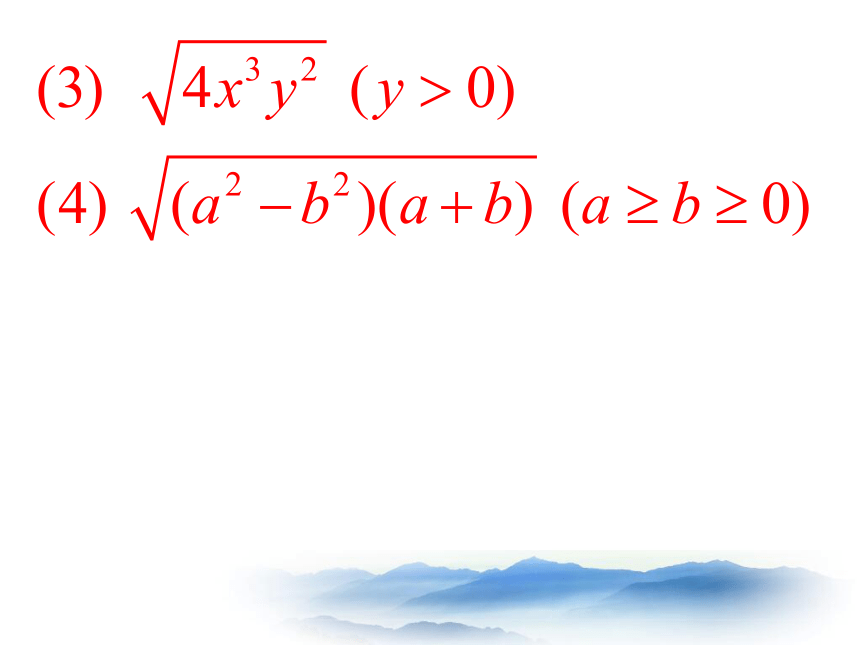






文档简介
(共32张PPT)
16.2 最简二次根式 和同类二次根式
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的各因式的指数都为1
(2)被开方数不含分母
最简二次根式的定义
16.2-1最简二次根式
判断下列各式是否为最简二次根式?
(5) ( );
(2) ( );
(3) ( );
(4) ( );
(1) ( );
(6) ( );
(7) ( );
√
×
×
× 课本P7
×
×
√
辨析训练一
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。
最简二次根式的解读:
例1 把下列各式化成最简二次根式:
(1) ; (2)
解(1)
(2)
例题选讲一
化简二次根式的步骤是:
1)把被开方数(或式)化成积的形式,即分解因式。
2)化去根号内的分母,即分母有理化。
3)将根号内能开得尽方的因数(式)开出来。
把下列各式化成最简二次根式:
(1)
(2)
练习一
上一页
例2 把下列各式化成最简二次根式:
(1) ;(2)
解(1)
(2)
例题选讲二
把下列各式化成最简二次根式:
(1) (2)
(3) (4)
练习二
上一页
判断下列各等式是否成立,若不成立请说出正确的解法和答案。
(1) ( )(2) ( )
(3) ( )(4) ( )
×
×
×
√
辨析训练二
上一页
把下列各式化成最简二次根式:
(1)
(2)
(3)
(4)
强化训练
上一页
你能发现其中的错误吗?
这节你学到了什么?
1.最简二次根式的概念.
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。
2.如何化二次根式为最简二次根式 .
课堂小结:
16.2-2同类二次根式
(1)被开方数中的各因数
的指数都为1。
(2)被开方数不含分母。
最简二次根式
温故知新
二次根式计算、化简的结果应符合什么要求?
观察思考
与
的形式与实质是什么?
形式上都是二次根式,实质上
不是最简二次根式,可以化简:
和
还可以化简吗?
二次根式的加减
这个就是我们今天要学习的内容
是最简二次根式
但
塔座
C
B
A
m
m
m
已知△ABC中,∠C=90°,
问题:
AB=
m
L等于多少呢?
BC=
m,那么△ABC的周长
要想知道周长L,必须先求出
AC长度,因为△ABC为Rt △,
所以可由勾股定理求得AC。
解:∵在△ABC中,∠C=90°,
∴利用勾股定理,可得:
(m)
故周长L=AB+BC+AC=
+
+
通过观察发现:
,
,
都不是最简二次根式
问题分析:
C
B
m
m
m
A
(化简)
(逆用分配律)
如何计算出这个结果呢?
于是得出二次根式加减法的一般思路:
经过化简以后有什么共同特征?
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式。
所以
周长L=AB+BC+AC
=
(m)
可化简得:
只有付出,才有回报
(1)如果几个二次根式的被开方数相同,那么可以直接根据分配律进行加减运算;
(2)如果所给的二次根式不是
最简二次根式,应该先化简,
再考虑进行加减运算。
二次根式加减法的一般思路:
理论应用
实践
要看几个二次根式是否为
同类二次根式,先将它们都化为
最简二次根式,再被开方数是否
相同。
例1 下列各式
,
中,哪些是同类二次根式?
,
,
,
,
,
分析:
,
,
,
,
。
解:∵
∴
,
是同类二次根式,
,
,
是同类二次根式,
,
是同类二次根式,
例1 下列各式
,
中,哪些是同类二次根式?
,
,
,
,
,
经过分析思考得出:
思考:判断同类二次根式与判断同类项有什么区别?
注意:判断几个二次根式是否为同类二次根式,只需看化为最简二次根式后的被开方数是否相同,与最简二次根式前面的因式及符号无关.
巩固提高
加深理解
1.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
125
2. 与 是同类二次根式的是( )
A. B. C. D.
D
火眼金睛
B
A
C
D
你真棒!
再接再励
B
A
C
很抱歉!
再思考一下
要细心哟!
再检查一下
注意:不是同类二次根式的
(如 与 )不能合并
3.判断:下列计算是否正确 为什么
开动你的脑筋,你一定行!
×
正确:
×
×
解:
先化简,
再合并
不是同类二次根式不能合并
小试牛刀
(4)下列计算正确的是( )
A.
D.
C.
B.
C
完全正确相信自己没错
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
交流 归纳
不要写成带分数
尝试与交流
计算
(1)
(2)
解:
(1)原式=
(2)原式
不是同类二次根式不能合并
硕果累累
一路下来,我们结识了很多新知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
1. 什么是同类二次根式?
几个二次根式化为最简二次根式以后,被开方数相同。
2.怎样进行二次根式的加减法运算?
一化二找三合并
讨论 总结
16.2 最简二次根式 和同类二次根式
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的各因式的指数都为1
(2)被开方数不含分母
最简二次根式的定义
16.2-1最简二次根式
判断下列各式是否为最简二次根式?
(5) ( );
(2) ( );
(3) ( );
(4) ( );
(1) ( );
(6) ( );
(7) ( );
√
×
×
× 课本P7
×
×
√
辨析训练一
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。
最简二次根式的解读:
例1 把下列各式化成最简二次根式:
(1) ; (2)
解(1)
(2)
例题选讲一
化简二次根式的步骤是:
1)把被开方数(或式)化成积的形式,即分解因式。
2)化去根号内的分母,即分母有理化。
3)将根号内能开得尽方的因数(式)开出来。
把下列各式化成最简二次根式:
(1)
(2)
练习一
上一页
例2 把下列各式化成最简二次根式:
(1) ;(2)
解(1)
(2)
例题选讲二
把下列各式化成最简二次根式:
(1) (2)
(3) (4)
练习二
上一页
判断下列各等式是否成立,若不成立请说出正确的解法和答案。
(1) ( )(2) ( )
(3) ( )(4) ( )
×
×
×
√
辨析训练二
上一页
把下列各式化成最简二次根式:
(1)
(2)
(3)
(4)
强化训练
上一页
你能发现其中的错误吗?
这节你学到了什么?
1.最简二次根式的概念.
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。
2.如何化二次根式为最简二次根式 .
课堂小结:
16.2-2同类二次根式
(1)被开方数中的各因数
的指数都为1。
(2)被开方数不含分母。
最简二次根式
温故知新
二次根式计算、化简的结果应符合什么要求?
观察思考
与
的形式与实质是什么?
形式上都是二次根式,实质上
不是最简二次根式,可以化简:
和
还可以化简吗?
二次根式的加减
这个就是我们今天要学习的内容
是最简二次根式
但
塔座
C
B
A
m
m
m
已知△ABC中,∠C=90°,
问题:
AB=
m
L等于多少呢?
BC=
m,那么△ABC的周长
要想知道周长L,必须先求出
AC长度,因为△ABC为Rt △,
所以可由勾股定理求得AC。
解:∵在△ABC中,∠C=90°,
∴利用勾股定理,可得:
(m)
故周长L=AB+BC+AC=
+
+
通过观察发现:
,
,
都不是最简二次根式
问题分析:
C
B
m
m
m
A
(化简)
(逆用分配律)
如何计算出这个结果呢?
于是得出二次根式加减法的一般思路:
经过化简以后有什么共同特征?
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式。
所以
周长L=AB+BC+AC
=
(m)
可化简得:
只有付出,才有回报
(1)如果几个二次根式的被开方数相同,那么可以直接根据分配律进行加减运算;
(2)如果所给的二次根式不是
最简二次根式,应该先化简,
再考虑进行加减运算。
二次根式加减法的一般思路:
理论应用
实践
要看几个二次根式是否为
同类二次根式,先将它们都化为
最简二次根式,再被开方数是否
相同。
例1 下列各式
,
中,哪些是同类二次根式?
,
,
,
,
,
分析:
,
,
,
,
。
解:∵
∴
,
是同类二次根式,
,
,
是同类二次根式,
,
是同类二次根式,
例1 下列各式
,
中,哪些是同类二次根式?
,
,
,
,
,
经过分析思考得出:
思考:判断同类二次根式与判断同类项有什么区别?
注意:判断几个二次根式是否为同类二次根式,只需看化为最简二次根式后的被开方数是否相同,与最简二次根式前面的因式及符号无关.
巩固提高
加深理解
1.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
125
2. 与 是同类二次根式的是( )
A. B. C. D.
D
火眼金睛
B
A
C
D
你真棒!
再接再励
B
A
C
很抱歉!
再思考一下
要细心哟!
再检查一下
注意:不是同类二次根式的
(如 与 )不能合并
3.判断:下列计算是否正确 为什么
开动你的脑筋,你一定行!
×
正确:
×
×
解:
先化简,
再合并
不是同类二次根式不能合并
小试牛刀
(4)下列计算正确的是( )
A.
D.
C.
B.
C
完全正确相信自己没错
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
交流 归纳
不要写成带分数
尝试与交流
计算
(1)
(2)
解:
(1)原式=
(2)原式
不是同类二次根式不能合并
硕果累累
一路下来,我们结识了很多新知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
1. 什么是同类二次根式?
几个二次根式化为最简二次根式以后,被开方数相同。
2.怎样进行二次根式的加减法运算?
一化二找三合并
讨论 总结
