人教版九年级数学上册同步练习:24.2.2切线的判定和性质(第2课时 Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册同步练习:24.2.2切线的判定和性质(第2课时 Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 187.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览



文档简介
24.2.2第2课时 切线的判定和性质
1.下列说法中正确的是( )
A.与圆有公共点的直线是圆的切线
B.到圆心的距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线
D.过圆的半径的外端的直线是圆的切线
2
如图,AB是☉O的直径,AC是☉O的切线,A为切点,BC与☉O交于点D,连接OD.若∠C=50°,则∠AOD的度数为( )
A.40°
B.50°
C.80°
D.100°
3
如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段BP的长为
( )
A.3
B.3
C.6
D.9
4
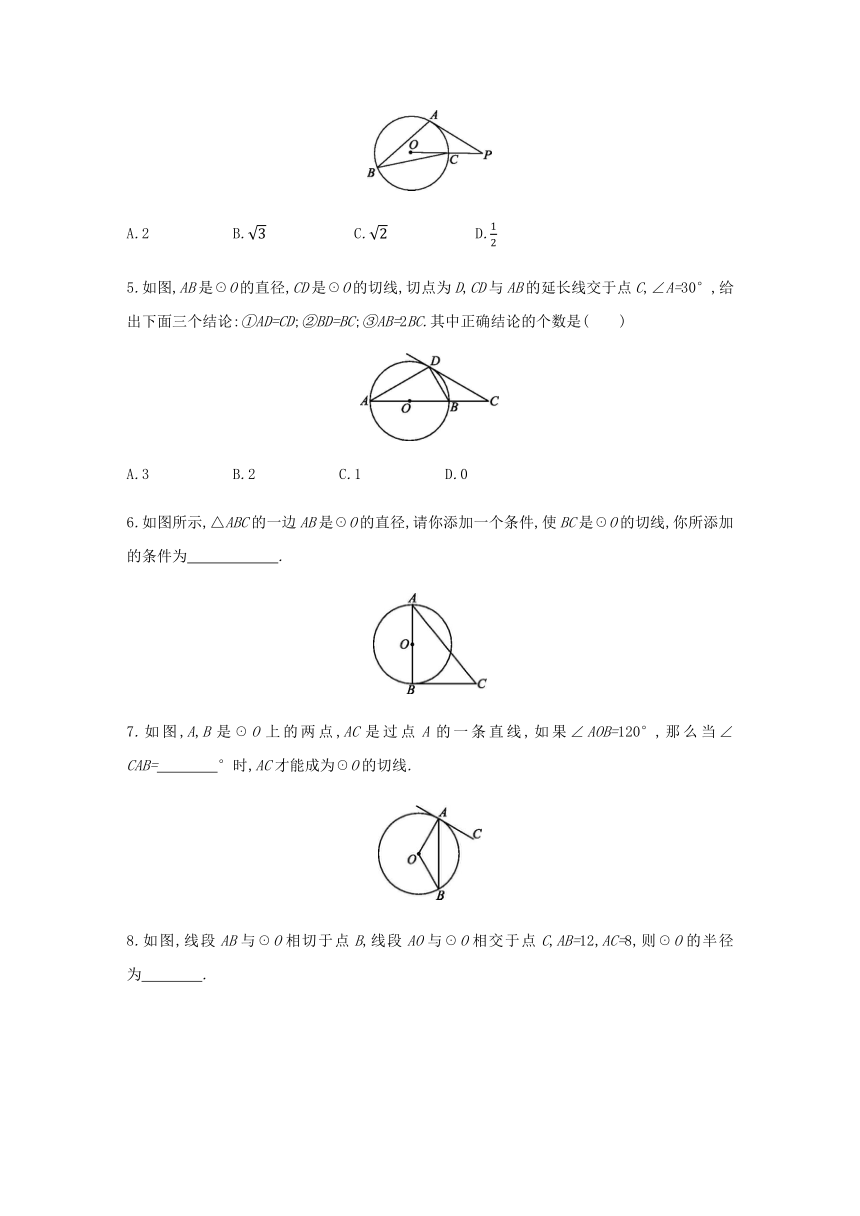
如图,已知☉O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.2
B.
C.
D.
5.如图,AB是☉O的直径,CD是☉O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面三个结论:①AD=CD;②BD=BC;③AB=2BC.其中正确结论的个数是( )
A.3
B.2
C.1
D.0
6.如图所示,△ABC的一边AB是☉O的直径,请你添加一个条件,使BC是☉O的切线,你所添加的条件为 .?
7.如图,A,B是☉O上的两点,AC是过点A的一条直线,如果∠AOB=120°,那么当∠CAB= °时,AC才能成为☉O的切线.?
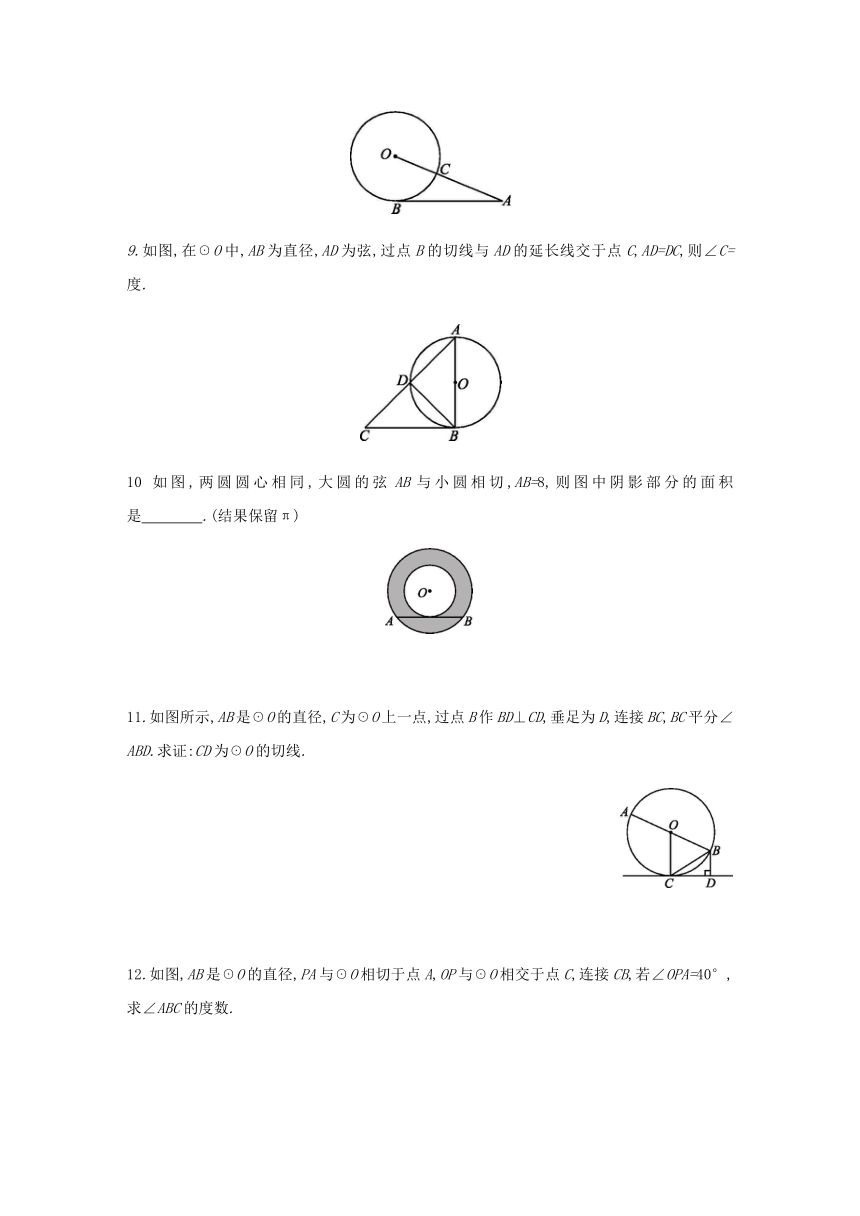
8.如图,线段AB与☉O相切于点B,线段AO与☉O相交于点C,AB=12,AC=8,则☉O的半径为 .?
9.如图,在☉O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C= 度.?
10
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是 .(结果保留π)?
11.如图所示,AB是☉O的直径,C为☉O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.求证:CD为☉O的切线.
12.如图,AB是☉O的直径,PA与☉O相切于点A,OP与☉O相交于点C,连接CB,若∠OPA=40°,求∠ABC的度数.
13.如图,AB是☉O的直径,C是☉O上一点,点D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是☉O的切线;
(2)若☉O的半径为3,CD=4,求BD的长.
14.如图,AB是☉O的直径,ED切☉O于点C,AD交☉O于点F,AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD=4,AF=2,求☉O的半径.
15.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,以CD为直径的☉O分别交AC,BC于点M,N,过点N作NE⊥AB,垂足为E.
(1)若☉O的半径为,AC=6,求BN的长;
(2)求证:NE与☉O相切.
答案
1-5.BCABA
6.答案不唯一,如∠ABC=90°
7.60
8.5 .
9.45 .
10.16π
11.证明:∵BC平分∠ABD,∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为☉O的切线.
12.解:∵AB是☉O的直径,PA与☉O相切于点A,∴∠BAP=90°.∵∠OPA=40°,
∴∠AOP=180°-90°-40°=50°,
∴∠ABC=∠AOP=×50°=25°.
13.解:(1)证明:如图,连接OC.∵AB是☉O的直径,C是☉O上一点,
∴∠ACB=90°,
即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴OC⊥CD.
又∵OC是☉O的半径,
∴CD是☉O的切线.
(2)由(1)及已知得∠OCD=90°,OB=OC=3,CD=4.
在Rt△OCD中,根据勾股定理,得OD=5,
∴BD=OD-OB=5-3=2.
14.解:(1)证明:连接OC,如图.
∵AC平分∠BAD,
∴∠1=∠2.
∵OA=OC,∴∠1=∠3,
∴∠2=∠3,
∴OC∥AD.
∵ED切☉O于点C,
∴OC⊥ED,∴AD⊥ED.
(2)设OC交BF于点H,如图.
∵AB为☉O的直径,∴∠AFB=90°,易得四边形CDFH为矩形,
∴FH=CD=4,∠CHF=90°,
∴OH⊥BF,∴BH=FH=4,∴BF=8.
在Rt△ABF中,AB===2,∴☉O的半径为.
15.解:(1)如图,连接DN,ON.
∵☉O的半径为,∴CD=5.
∵∠ACB=90°,CD是斜边AB上的中线,
∴BD=CD=AD=5,
∴AB=10,
∴BC==8.
∵CD为直径,∴∠CND=90°.
又∵BD=CD,∴BN=NC=4.
(2)证明:∵∠ACB=90°,CD为斜边AB上的中线,
∴CD=AD=BD=AB,
∴∠BCD=∠B.
∵OC=ON,∴∠BCD=∠ONC,
∴∠ONC=∠B,
∴ON∥AB.
∵NE⊥AB,
∴ON⊥NE,∴NE与☉O相切.
1.下列说法中正确的是( )
A.与圆有公共点的直线是圆的切线
B.到圆心的距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线
D.过圆的半径的外端的直线是圆的切线
2
如图,AB是☉O的直径,AC是☉O的切线,A为切点,BC与☉O交于点D,连接OD.若∠C=50°,则∠AOD的度数为( )
A.40°
B.50°
C.80°
D.100°
3
如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段BP的长为
( )
A.3
B.3
C.6
D.9
4
如图,已知☉O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.2
B.
C.
D.
5.如图,AB是☉O的直径,CD是☉O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面三个结论:①AD=CD;②BD=BC;③AB=2BC.其中正确结论的个数是( )
A.3
B.2
C.1
D.0
6.如图所示,△ABC的一边AB是☉O的直径,请你添加一个条件,使BC是☉O的切线,你所添加的条件为 .?
7.如图,A,B是☉O上的两点,AC是过点A的一条直线,如果∠AOB=120°,那么当∠CAB= °时,AC才能成为☉O的切线.?
8.如图,线段AB与☉O相切于点B,线段AO与☉O相交于点C,AB=12,AC=8,则☉O的半径为 .?
9.如图,在☉O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C= 度.?
10
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是 .(结果保留π)?
11.如图所示,AB是☉O的直径,C为☉O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.求证:CD为☉O的切线.
12.如图,AB是☉O的直径,PA与☉O相切于点A,OP与☉O相交于点C,连接CB,若∠OPA=40°,求∠ABC的度数.
13.如图,AB是☉O的直径,C是☉O上一点,点D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是☉O的切线;
(2)若☉O的半径为3,CD=4,求BD的长.
14.如图,AB是☉O的直径,ED切☉O于点C,AD交☉O于点F,AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD=4,AF=2,求☉O的半径.
15.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,以CD为直径的☉O分别交AC,BC于点M,N,过点N作NE⊥AB,垂足为E.
(1)若☉O的半径为,AC=6,求BN的长;
(2)求证:NE与☉O相切.
答案
1-5.BCABA
6.答案不唯一,如∠ABC=90°
7.60
8.5 .
9.45 .
10.16π
11.证明:∵BC平分∠ABD,∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为☉O的切线.
12.解:∵AB是☉O的直径,PA与☉O相切于点A,∴∠BAP=90°.∵∠OPA=40°,
∴∠AOP=180°-90°-40°=50°,
∴∠ABC=∠AOP=×50°=25°.
13.解:(1)证明:如图,连接OC.∵AB是☉O的直径,C是☉O上一点,
∴∠ACB=90°,
即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴OC⊥CD.
又∵OC是☉O的半径,
∴CD是☉O的切线.
(2)由(1)及已知得∠OCD=90°,OB=OC=3,CD=4.
在Rt△OCD中,根据勾股定理,得OD=5,
∴BD=OD-OB=5-3=2.
14.解:(1)证明:连接OC,如图.
∵AC平分∠BAD,
∴∠1=∠2.
∵OA=OC,∴∠1=∠3,
∴∠2=∠3,
∴OC∥AD.
∵ED切☉O于点C,
∴OC⊥ED,∴AD⊥ED.
(2)设OC交BF于点H,如图.
∵AB为☉O的直径,∴∠AFB=90°,易得四边形CDFH为矩形,
∴FH=CD=4,∠CHF=90°,
∴OH⊥BF,∴BH=FH=4,∴BF=8.
在Rt△ABF中,AB===2,∴☉O的半径为.
15.解:(1)如图,连接DN,ON.
∵☉O的半径为,∴CD=5.
∵∠ACB=90°,CD是斜边AB上的中线,
∴BD=CD=AD=5,
∴AB=10,
∴BC==8.
∵CD为直径,∴∠CND=90°.
又∵BD=CD,∴BN=NC=4.
(2)证明:∵∠ACB=90°,CD为斜边AB上的中线,
∴CD=AD=BD=AB,
∴∠BCD=∠B.
∵OC=ON,∴∠BCD=∠ONC,
∴∠ONC=∠B,
∴ON∥AB.
∵NE⊥AB,
∴ON⊥NE,∴NE与☉O相切.
同课章节目录
