华东师大版八年级上册11.2实数课件(32张张PPT)
文档属性
| 名称 | 华东师大版八年级上册11.2实数课件(32张张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 17:11:27 | ||
图片预览








文档简介
(共32张PPT)
学而不疑则怠,疑而不探则空
第四节
实数一
华师版八年级上学期
第十一章
《数的开方》
把下列各数填入相应的集合内:
1.整数集合:
2.分数集合:
3.有理数集合:
有理数包括整数和分数.而任何一个分数写成小数形式,必定是有限小数或无限循环小数.
温故知新
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949…
π是无限不循环的小数.
1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605714701095599716059702745345968620147285174186408891986095523292304843087143214508397626036279952514079896872533965463318088296406206152583523950547457502877599617298355752203375318570113543746034084988471603868999706990048150305440277903164542478230684929369186215805…
是无限不循环的小数.
像
等都是无理数.
无限不循环小数叫做无理数.
有理数和无理数统称实
数.
概括
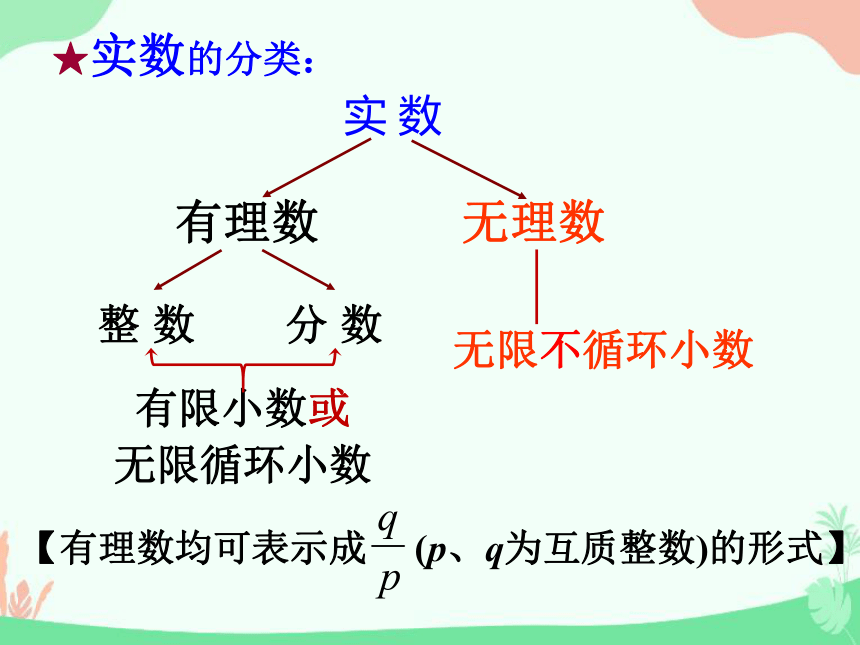
★实数的分类:
实
数
有理数
无理数
整
数
分
数
有限小数或
无限循环小数
【有理数均可表示成
(p、q为互质整数)的形式】
无限不循环小数
(1)有根号且开方开不尽的.如:
无理数的三种表达形式:
(3)无限不循环小数.如:
(2)含有π的.如:
3.14159…,-1.4142…,0.8080080008…
负实数
正实数
数实
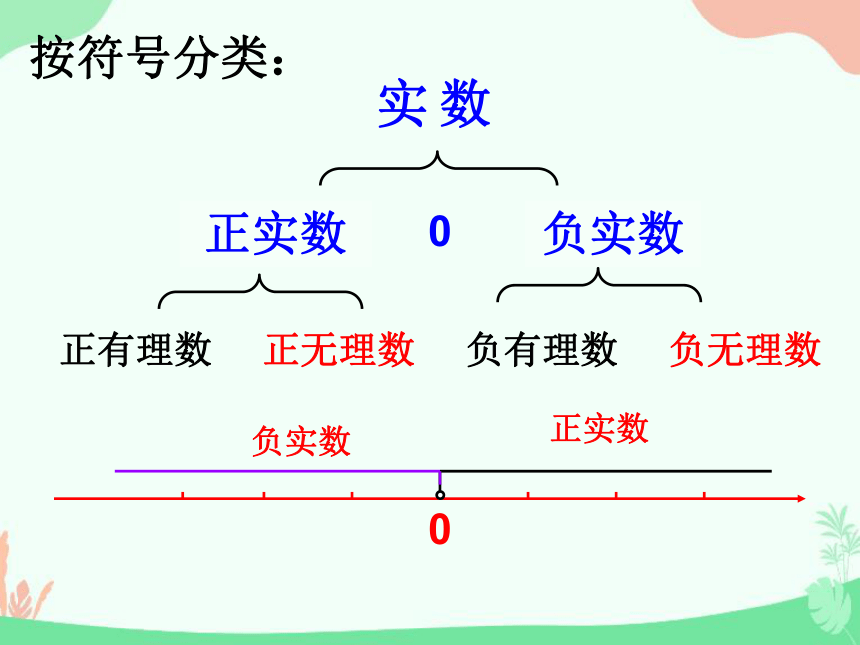
正有理数
负有理数
按符号分类:
0
正无理数
负无理数
0
正实数
负实数
下列说法正确吗?请说明理由.
(1)3.14159是无理数;
(2)无限小数都是无理数;
(3)无理数都是无限小数;
解:(1)错误.因为无理数是无限不循环小数,
而3.14159是有限小数,故它不是无理数。
(2)错误.因为无限小数包括无限循环小数和无限不循环小数,其中无限不循环小数才是无理数,故正确说法应为“无限小数包含无理数”。
(3)正确.因为无理数是无限不循环小数,
所以无理数都是无限小数。
(4)带根号的数都是无理数;
解:错误.比如
带有根号,但它是有理数3.
正确说法应为:
带有根号且开方开不尽的数才是无理数.
(5)无理数都是开方开不尽的数;
解:错误.因为无理数有三种表达形式,开方
开不
尽的数只是其中一种,正确说法应
为“无理数包括开方开不尽的数”。
(6)不循环小数都是无理数.
解:错误.因为不循环小数包括有限不循环小数和无限不循环小数,只有无限不循环小数才是无理数。
-4
-2
0
1
2
3
4
-1
-3
π
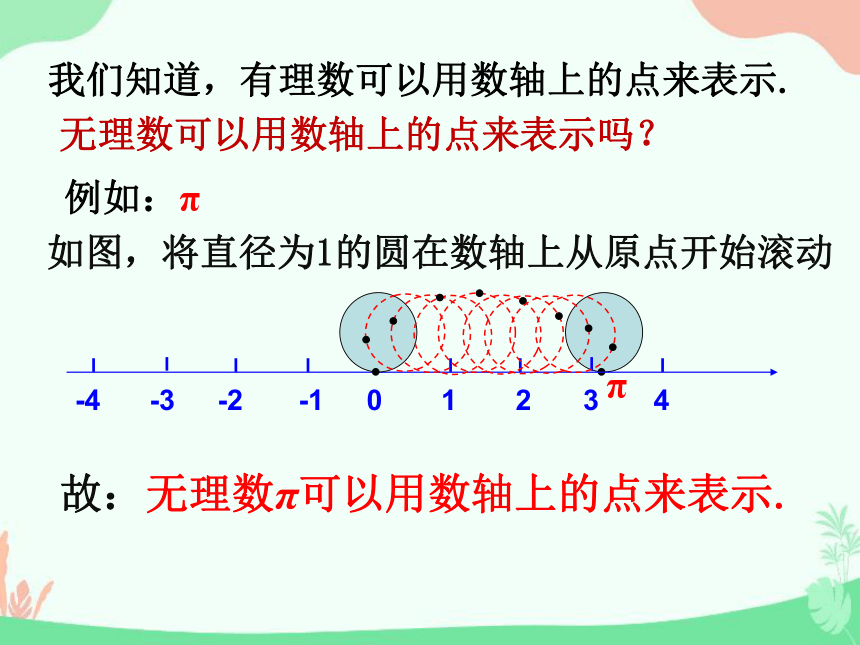
我们知道,有理数可以用数轴上的点来表示.
无理数可以用数轴上的点来表示吗?
如图,将直径为1的圆在数轴上从原点开始滚动
例如:π
故:无理数π可以用数轴上的点来表示.
1
1
1
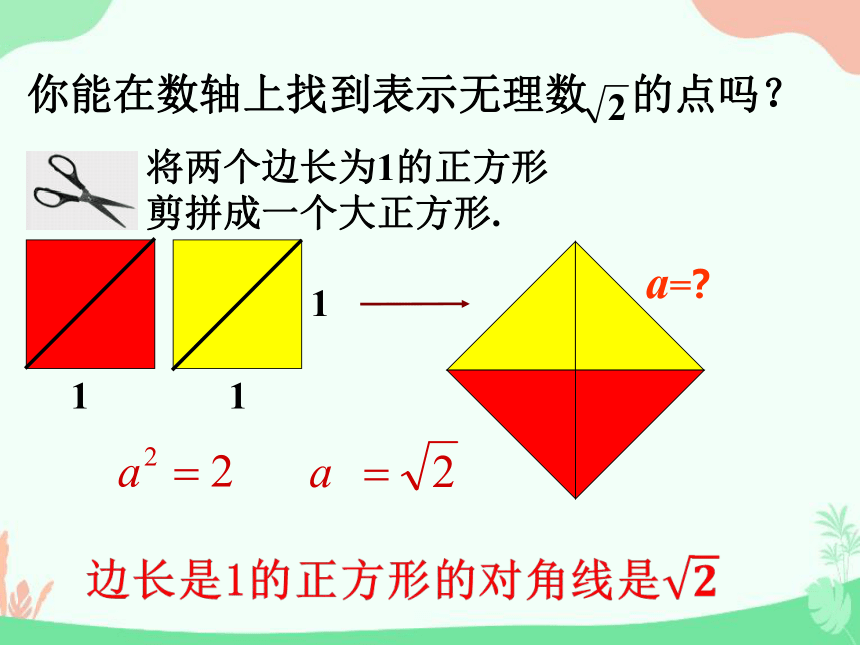
你能在数轴上找到表示无理数
的点吗?
将两个边长为1的正方形
剪拼成一个大正方形.
a=?
0
1
-1
在数轴上找表示
、
的点
故:无理数
可以用数轴上的点来表示.
数轴上的每一个点必定表示一个实数;反之,每一个实数都可以用数轴上的一个点来表示.即:
实数与数轴上的点一一对应.
同学们在以后的学习中可以证明这个结论的哟!
概括
1、把下列各数分别填入相应的数集里:
实数集{
…
}
无理数集{
…
}
有理数集{
…
}
分数集{
…
}
负无理数{
…
}
一、基础巩固:
课后作业
2、下列说法正确吗?请说明理由.
(1)
是分数;
(2)因为π≈3.14159,而3.14159是有理数,
所以π是有理数;
(3)有理数可以通过开方运算得到无理数,则无理数都可以通过乘方得到有理数.
二、拓展探究:
(1)阅读下列材料:
∵
在整数1和2之间,
∴
的整数部分是1,
小数部分是
-1.
∵
在整数-2和-1之间,
∴
的整数部分是-1,
小数部分是
+1.
(2)根据上面的材料,写出下列各无理数的
整数部分和小数部分:
学而不疑则怠,疑而不探则空
第五节
实数二
华师版八年级上学期
第十一章
《数的开方》
1.请将数轴上各点与下列实数对应起来.
-3
-2
-1
0
1
2
3
4
A
B
C
D
E
4
2.下列实数中,无理数是(
)
A.
3.14
B.
C.
0
D.
D
温故知新
3.下列各组数中,互为相反数的一组是(
)
5.在数轴上与原点距离等于
的点表示的数
是(
)
A.
-3
与
B.
-3与-
C.
|-3|与
D.
-3与
4.下列各数中,介于6和7之间的数是(
)
D
B
C
A.
B.
C.
D.
A.
B.
C.
D.
7和-7
说明:
有关有理数的相反数、绝对值等概念、大小比较法则、运算法则以及运算律,
对于实数也适用.
例1:
说出下列实数的相反数、绝对值:
实数
相反数
绝对值
(a<3)
例2:
比较下列各组实数的大小:
与
取近似值法
★实数的大小比较
1.借助数轴(左小右大);
2.借助绝对值
(两个负数比较,绝对值大的反而小);
3.借助计算器进行近似计算(适用于无理数);
4.乘方法;5.差值比较法;6.商值比较法;
7.倒数比较;8.规律法.
例3:
计算:(结果精确到0.01)
解:
原式=
=
≈
1.414+0.333+6.284
=
8.031
≈
8.03
说明:
从有理数扩充到实数以后,正数总可以开方.在实数范围内,任意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.任意一个实数有且只有一个立方根.
例4:
填空:
(1)
3是非负数
的平方.
(2)
2的算术平方根的平方是
;
5的立方根的立方是
.
解析:
根据乘方和开方互为逆运算,可得
分组讨论
1、填空:
2、比较下列各组实数的大小:
例5:
小聪用下面的方法求实数
的近似值(精确到0.1):
∵9<10<16
即
3<
<4
∴3.1<
<3.2
故
的整数部分是3.
由3.32=10.89>10,
3.22=10.24>10,
3.12=9.61<10,
∴
<
<
而3.152=9.9225<10,
∴实数
的近似值为3.2
第一步:
确定整数部分
第二步:
逐步缩小范围
用同样的方法求下列实数的近似值(精确到0.1)
:
课本P11练习题
课堂练习:
(1)不正确.因为两个整数相除,商必定为有理数.当除不尽时,其结果是一个无限循环小数.
1、判断题:
(2)正确.因为任何实数的绝对值都是非负数,而无理数不包含0,所以任何一个无理数的绝对值都是正数.
2、计算题:
3、比较大小:
而12<18
∴
<
而-1.323<-1.047
∴
<
实数与数轴上的点一一对应.
无限不循环小数叫做无理数.有理数和无理数统称实数.
有关有理数的相反数、绝对值等概念、大小比较法则、运算法则以及运算律,对于实数也适用.
补充说明:对无理数取近似值,
一般精确到千分位.
课堂小结:
课本P11习题11.2
一、基础巩固:
课后作业
二、提高练习:
1、不用计算器,比较下列实数的大小:
2、已知非负数a、b、c满足:a2=2,b的立方根和算术平方根都是本身,c的相反数为
,判断以a、b、c为三边长能否组成三角形?
学而不疑则怠,疑而不探则空
第四节
实数一
华师版八年级上学期
第十一章
《数的开方》
把下列各数填入相应的集合内:
1.整数集合:
2.分数集合:
3.有理数集合:
有理数包括整数和分数.而任何一个分数写成小数形式,必定是有限小数或无限循环小数.
温故知新
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949…
π是无限不循环的小数.
1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605714701095599716059702745345968620147285174186408891986095523292304843087143214508397626036279952514079896872533965463318088296406206152583523950547457502877599617298355752203375318570113543746034084988471603868999706990048150305440277903164542478230684929369186215805…
是无限不循环的小数.
像
等都是无理数.
无限不循环小数叫做无理数.
有理数和无理数统称实
数.
概括
★实数的分类:
实
数
有理数
无理数
整
数
分
数
有限小数或
无限循环小数
【有理数均可表示成
(p、q为互质整数)的形式】
无限不循环小数
(1)有根号且开方开不尽的.如:
无理数的三种表达形式:
(3)无限不循环小数.如:
(2)含有π的.如:
3.14159…,-1.4142…,0.8080080008…
负实数
正实数
数实
正有理数
负有理数
按符号分类:
0
正无理数
负无理数
0
正实数
负实数
下列说法正确吗?请说明理由.
(1)3.14159是无理数;
(2)无限小数都是无理数;
(3)无理数都是无限小数;
解:(1)错误.因为无理数是无限不循环小数,
而3.14159是有限小数,故它不是无理数。
(2)错误.因为无限小数包括无限循环小数和无限不循环小数,其中无限不循环小数才是无理数,故正确说法应为“无限小数包含无理数”。
(3)正确.因为无理数是无限不循环小数,
所以无理数都是无限小数。
(4)带根号的数都是无理数;
解:错误.比如
带有根号,但它是有理数3.
正确说法应为:
带有根号且开方开不尽的数才是无理数.
(5)无理数都是开方开不尽的数;
解:错误.因为无理数有三种表达形式,开方
开不
尽的数只是其中一种,正确说法应
为“无理数包括开方开不尽的数”。
(6)不循环小数都是无理数.
解:错误.因为不循环小数包括有限不循环小数和无限不循环小数,只有无限不循环小数才是无理数。
-4
-2
0
1
2
3
4
-1
-3
π
我们知道,有理数可以用数轴上的点来表示.
无理数可以用数轴上的点来表示吗?
如图,将直径为1的圆在数轴上从原点开始滚动
例如:π
故:无理数π可以用数轴上的点来表示.
1
1
1
你能在数轴上找到表示无理数
的点吗?
将两个边长为1的正方形
剪拼成一个大正方形.
a=?
0
1
-1
在数轴上找表示
、
的点
故:无理数
可以用数轴上的点来表示.
数轴上的每一个点必定表示一个实数;反之,每一个实数都可以用数轴上的一个点来表示.即:
实数与数轴上的点一一对应.
同学们在以后的学习中可以证明这个结论的哟!
概括
1、把下列各数分别填入相应的数集里:
实数集{
…
}
无理数集{
…
}
有理数集{
…
}
分数集{
…
}
负无理数{
…
}
一、基础巩固:
课后作业
2、下列说法正确吗?请说明理由.
(1)
是分数;
(2)因为π≈3.14159,而3.14159是有理数,
所以π是有理数;
(3)有理数可以通过开方运算得到无理数,则无理数都可以通过乘方得到有理数.
二、拓展探究:
(1)阅读下列材料:
∵
在整数1和2之间,
∴
的整数部分是1,
小数部分是
-1.
∵
在整数-2和-1之间,
∴
的整数部分是-1,
小数部分是
+1.
(2)根据上面的材料,写出下列各无理数的
整数部分和小数部分:
学而不疑则怠,疑而不探则空
第五节
实数二
华师版八年级上学期
第十一章
《数的开方》
1.请将数轴上各点与下列实数对应起来.
-3
-2
-1
0
1
2
3
4
A
B
C
D
E
4
2.下列实数中,无理数是(
)
A.
3.14
B.
C.
0
D.
D
温故知新
3.下列各组数中,互为相反数的一组是(
)
5.在数轴上与原点距离等于
的点表示的数
是(
)
A.
-3
与
B.
-3与-
C.
|-3|与
D.
-3与
4.下列各数中,介于6和7之间的数是(
)
D
B
C
A.
B.
C.
D.
A.
B.
C.
D.
7和-7
说明:
有关有理数的相反数、绝对值等概念、大小比较法则、运算法则以及运算律,
对于实数也适用.
例1:
说出下列实数的相反数、绝对值:
实数
相反数
绝对值
(a<3)
例2:
比较下列各组实数的大小:
与
取近似值法
★实数的大小比较
1.借助数轴(左小右大);
2.借助绝对值
(两个负数比较,绝对值大的反而小);
3.借助计算器进行近似计算(适用于无理数);
4.乘方法;5.差值比较法;6.商值比较法;
7.倒数比较;8.规律法.
例3:
计算:(结果精确到0.01)
解:
原式=
=
≈
1.414+0.333+6.284
=
8.031
≈
8.03
说明:
从有理数扩充到实数以后,正数总可以开方.在实数范围内,任意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.任意一个实数有且只有一个立方根.
例4:
填空:
(1)
3是非负数
的平方.
(2)
2的算术平方根的平方是
;
5的立方根的立方是
.
解析:
根据乘方和开方互为逆运算,可得
分组讨论
1、填空:
2、比较下列各组实数的大小:
例5:
小聪用下面的方法求实数
的近似值(精确到0.1):
∵9<10<16
即
3<
<4
∴3.1<
<3.2
故
的整数部分是3.
由3.32=10.89>10,
3.22=10.24>10,
3.12=9.61<10,
∴
<
<
而3.152=9.9225<10,
∴实数
的近似值为3.2
第一步:
确定整数部分
第二步:
逐步缩小范围
用同样的方法求下列实数的近似值(精确到0.1)
:
课本P11练习题
课堂练习:
(1)不正确.因为两个整数相除,商必定为有理数.当除不尽时,其结果是一个无限循环小数.
1、判断题:
(2)正确.因为任何实数的绝对值都是非负数,而无理数不包含0,所以任何一个无理数的绝对值都是正数.
2、计算题:
3、比较大小:
而12<18
∴
<
而-1.323<-1.047
∴
<
实数与数轴上的点一一对应.
无限不循环小数叫做无理数.有理数和无理数统称实数.
有关有理数的相反数、绝对值等概念、大小比较法则、运算法则以及运算律,对于实数也适用.
补充说明:对无理数取近似值,
一般精确到千分位.
课堂小结:
课本P11习题11.2
一、基础巩固:
课后作业
二、提高练习:
1、不用计算器,比较下列实数的大小:
2、已知非负数a、b、c满足:a2=2,b的立方根和算术平方根都是本身,c的相反数为
,判断以a、b、c为三边长能否组成三角形?
