华东师大版八年级数学上册11.1.1平方根——算术平方根课件(共16张PPT)
文档属性
| 名称 | 华东师大版八年级数学上册11.1.1平方根——算术平方根课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 982.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 14:11:29 | ||
图片预览






文档简介
(共16张PPT)
学而不疑则怠,疑而不探则空
第二节
算术平方根
华师版八年级上学期
第十一章
《数的开方》
一、知识点回顾:
1、如果一个数的平方是a,那么这个数叫a的平方根。
2、一个正数的平方根有2个(互为相反数);
0的平方根有1个,是0;负数没有平方根。
3、平方和开平方运算有什么区别和联系?
区别:
(1)平方运算中,已知的是底数和指数,求的是幂;而在开平方运算中,已知的是幂和指数,求底数。
(2)平方运算中的底数可以是任意数,平方的结果是唯一的;而在开平方运算中,被开方数是非负数,开平方的结果不一定是唯一的。
联系:二者互为逆运算。
温故知新
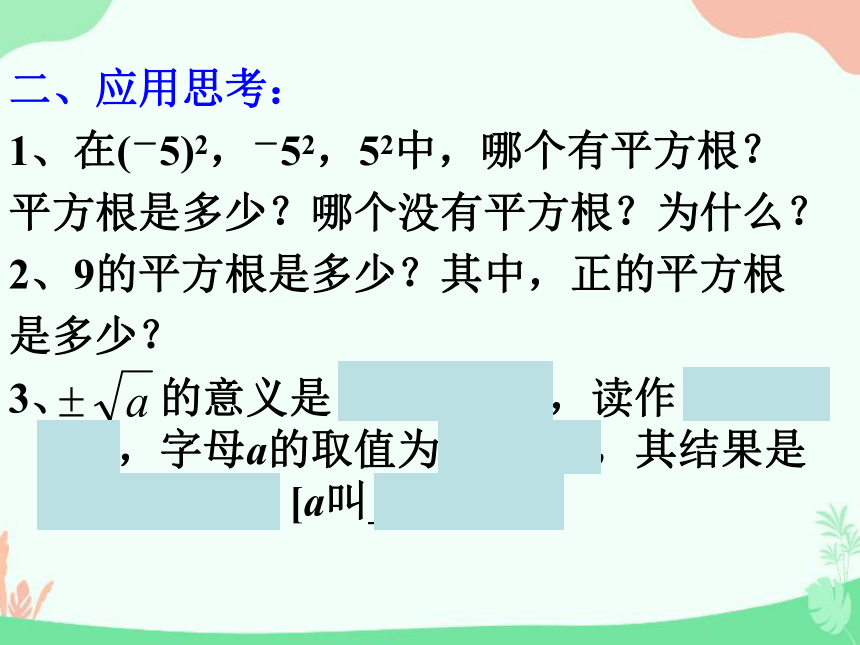
二、应用思考:
1、在(-5)2,-52,52中,哪个有平方根?
平方根是多少?哪个没有平方根?为什么?
2、9的平方根是多少?其中,正的平方根
是多少?
3、
的意义是
对a开平方
,读作
正负根号a
,字母a的取值为
非负数
,其结果是
a的平方根
。[a叫
被开方数]
1、
表示的意义是什么?
呢?
合作探究
正数a的正的平方根叫a的算术平方根.
答:
表示9的正的平方根;
表示9的负的平方根.
记作:
读作:
根号a
另一个平方根是它的相反数,即
规定:0的平方根也叫0的算术平方根.
即
合作探究
2、
存在的条件是什么?其结果是什么数?
存在的条件是a≥0,其结果是非负数.
即
≥0(其中a≥0)
1、求下列各数的平方根和算术平方根:
(1)49
(2)2.89
(3)
(4)
基础练习
解:(1)∵(±7)2=49,
∴49的平方根是±7,算术平方根是7.
而
的平方根是
的平方根是
,算术平方根是
.
2、说说下列各式表示的意义并化简:
解:(1)
(4)
表示求4与
的差的平方根,
2
.
1
9
表示求100的算术平方根,
(2)
表示求144的算术平方根的相反数,
(3)
表示求625的平方根,
理解提高
3、下列各式有意义吗?
解:∵无论a为何值,a2≥0,(-a)2≥0,
但
要有意义,必须满足
-a≥0,即a≤0.
要有意义,必须满足a=0.
解:(1)由2x≥0,解得x≥0.
故当a≤0时,
有意义.
(2)由-a≥0,解得a≤0.
故当x≥0时,
有意义.
(3)由x-1≥0,解得x≥1.
故当x≥1时,
有意义.
(4)∵无论a取何值,|-a|恒大等于0.
∴a为任意有理数,
均有意义.
知识小结
1、正数a的正的平方根叫a的算术平方根.
规定:0的算术平方根为0.
2、
≥0(其中a≥0)
1、求下列各数的平方根和算术平方根:
①0.36
②25600
③576
④0
2、计算:
课后作业
一、基础巩固:
3、
的平方根是多少?
二、拓展提高:
1、已知x是25的算术平方根,y是4的负的平方根,求下列代数式的值:
(1)yx
(2)(2x-3y)2
2、若某正数的平方根为2a+3和a-15,求这个数。
3、
4、
互查
挑战极限
试区别
与
.
精品阅读
用短除法求一个正数的算术平方根
3
1
.00'00'00
1
1
2
00
.
1×20
8
+8=28
+7=27
7
1
89
11
00
17×20
3
+3=343
10
29
7
1
00
173×20
2
+2=3462
69
24
1
72
方根的首位
3是被开方数
过渡值
每次补两个0
误差值
1.732是3的算术平方根
亲爱的同学们,你看懂了吗?试试用短除法求下列数的算术平方根:2,5,6,7,8,10
天天都进步,真呀真快乐!
学而不疑则怠,疑而不探则空
第二节
算术平方根
华师版八年级上学期
第十一章
《数的开方》
一、知识点回顾:
1、如果一个数的平方是a,那么这个数叫a的平方根。
2、一个正数的平方根有2个(互为相反数);
0的平方根有1个,是0;负数没有平方根。
3、平方和开平方运算有什么区别和联系?
区别:
(1)平方运算中,已知的是底数和指数,求的是幂;而在开平方运算中,已知的是幂和指数,求底数。
(2)平方运算中的底数可以是任意数,平方的结果是唯一的;而在开平方运算中,被开方数是非负数,开平方的结果不一定是唯一的。
联系:二者互为逆运算。
温故知新
二、应用思考:
1、在(-5)2,-52,52中,哪个有平方根?
平方根是多少?哪个没有平方根?为什么?
2、9的平方根是多少?其中,正的平方根
是多少?
3、
的意义是
对a开平方
,读作
正负根号a
,字母a的取值为
非负数
,其结果是
a的平方根
。[a叫
被开方数]
1、
表示的意义是什么?
呢?
合作探究
正数a的正的平方根叫a的算术平方根.
答:
表示9的正的平方根;
表示9的负的平方根.
记作:
读作:
根号a
另一个平方根是它的相反数,即
规定:0的平方根也叫0的算术平方根.
即
合作探究
2、
存在的条件是什么?其结果是什么数?
存在的条件是a≥0,其结果是非负数.
即
≥0(其中a≥0)
1、求下列各数的平方根和算术平方根:
(1)49
(2)2.89
(3)
(4)
基础练习
解:(1)∵(±7)2=49,
∴49的平方根是±7,算术平方根是7.
而
的平方根是
的平方根是
,算术平方根是
.
2、说说下列各式表示的意义并化简:
解:(1)
(4)
表示求4与
的差的平方根,
2
.
1
9
表示求100的算术平方根,
(2)
表示求144的算术平方根的相反数,
(3)
表示求625的平方根,
理解提高
3、下列各式有意义吗?
解:∵无论a为何值,a2≥0,(-a)2≥0,
但
要有意义,必须满足
-a≥0,即a≤0.
要有意义,必须满足a=0.
解:(1)由2x≥0,解得x≥0.
故当a≤0时,
有意义.
(2)由-a≥0,解得a≤0.
故当x≥0时,
有意义.
(3)由x-1≥0,解得x≥1.
故当x≥1时,
有意义.
(4)∵无论a取何值,|-a|恒大等于0.
∴a为任意有理数,
均有意义.
知识小结
1、正数a的正的平方根叫a的算术平方根.
规定:0的算术平方根为0.
2、
≥0(其中a≥0)
1、求下列各数的平方根和算术平方根:
①0.36
②25600
③576
④0
2、计算:
课后作业
一、基础巩固:
3、
的平方根是多少?
二、拓展提高:
1、已知x是25的算术平方根,y是4的负的平方根,求下列代数式的值:
(1)yx
(2)(2x-3y)2
2、若某正数的平方根为2a+3和a-15,求这个数。
3、
4、
互查
挑战极限
试区别
与
.
精品阅读
用短除法求一个正数的算术平方根
3
1
.00'00'00
1
1
2
00
.
1×20
8
+8=28
+7=27
7
1
89
11
00
17×20
3
+3=343
10
29
7
1
00
173×20
2
+2=3462
69
24
1
72
方根的首位
3是被开方数
过渡值
每次补两个0
误差值
1.732是3的算术平方根
亲爱的同学们,你看懂了吗?试试用短除法求下列数的算术平方根:2,5,6,7,8,10
天天都进步,真呀真快乐!
