五年级上册数学课件-8 用字母表示数苏教版 (共27张PPT)
文档属性
| 名称 | 五年级上册数学课件-8 用字母表示数苏教版 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 21:54:35 | ||
图片预览






文档简介
(共27张PPT)
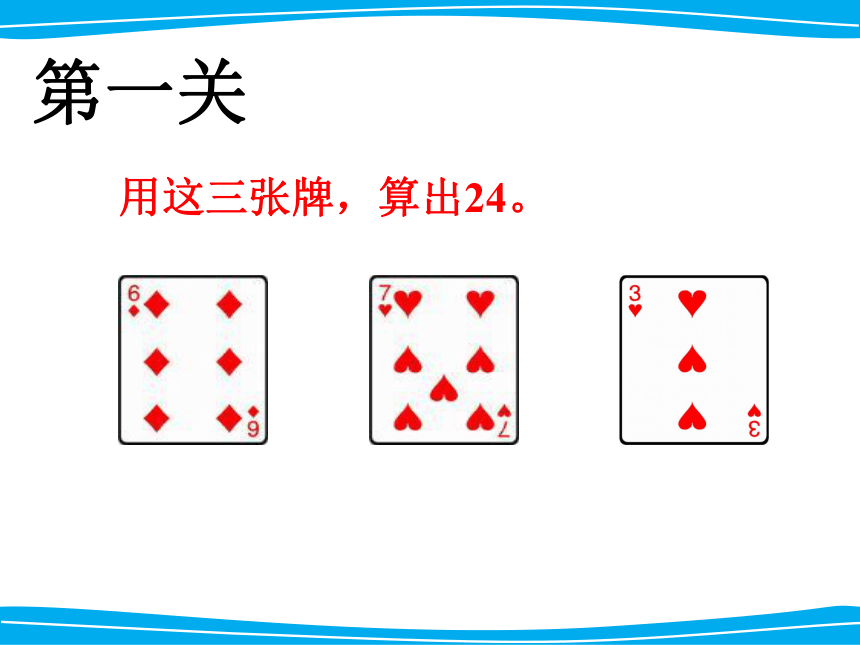
用这三张牌,算出24。
第一关
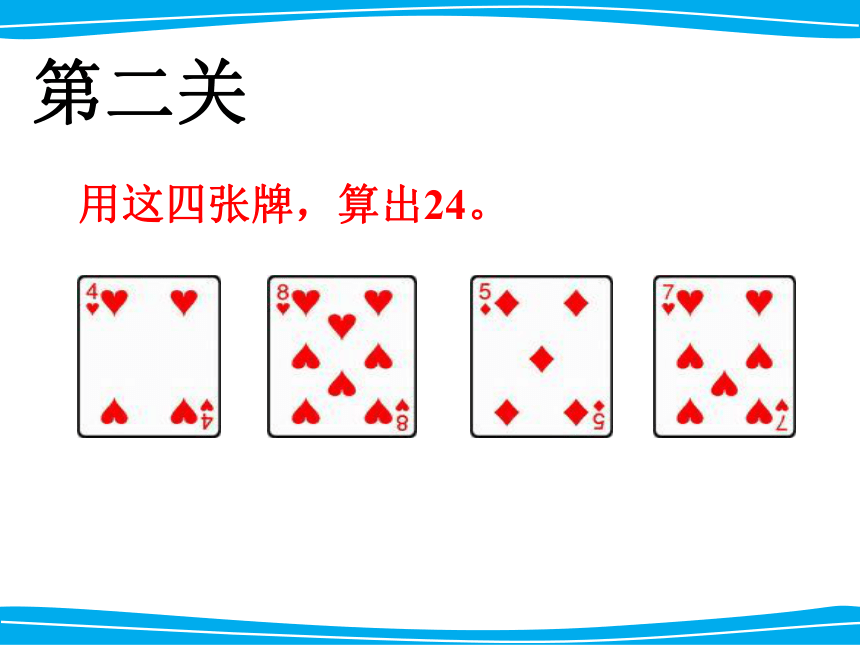
用这四张牌,算出24。
第二关
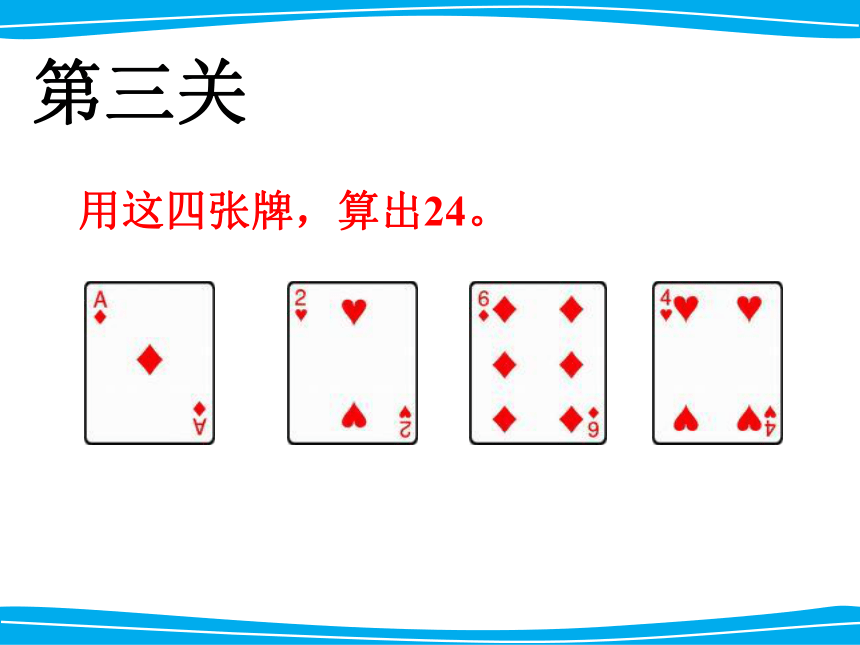
用这四张牌,算出24。
第三关
J
Q
K
1
12
11
13
A
1
2
放入硬币/枚
出来硬币/枚
2
4
1
2
放入硬币/枚
出来硬币/枚
3
6
2
4
1
2
放入硬币/枚
出来硬币/枚
3
6
2
4
1
2
放入硬币/枚
出来硬币/枚
……
你能想办法把所有的情况都表示出来吗?
3
6
2
4
1
2
放入硬币/枚
出来硬币/枚
……
×2
1
4
放入硬币/枚
出来硬币/枚
2
5
1
4
放入硬币/枚
出来硬币/枚
3
6
2
5
1
4
放入硬币/枚
出来硬币/枚
3
6
2
5
1
4
放入硬币/枚
出来硬币/枚
……
你能想办法把所有的情况表示出来吗?
3
6
2
5
1
4
放入硬币/枚
出来硬币/枚
……
+3
一个含有字母的式子不仅能表示一个数量,还能表示一个数量关系。
回顾思考:
①字母可以表示怎样的数?
②含有字母的式子可以表示什么?
③用字母和含有字母的式子来表示有什么好处?
1、甲、乙两地之间的公路长280千米,一辆汽车从甲地开往乙地。(只列式不计算)
已经行驶了50千米,剩下的千米数是
280-50;
已经行驶了74.5千米,剩下的千米数是
280-74.5;
已经行驶了b千米,剩下的千米数是
280-b
。
剩下的路程=
全长-已经行驶的路程
280-b
=160
280-b
=80
(
×b)×c=
×(b×c)
三个数相乘,先把前两个数相乘,再和第三个数相乘;或者先把后两个数相乘,再和第一个数相乘,积不变。
乘法结合律
加法结合律
×b=b×
两个数相乘,交换两个乘数的位置,积不变。
加法交换律
+b=b+
两个数相加,交换两个乘加数的位置,和不变。
乘法交换律
(
+b)+c=
+(b+c)
三个数相加,先把前两个数相加,再和第三个数相加;或者先把后两个数相加,再和第一个数相加,和不变。
乘法结合律
(
×b)×c=
×(b×c)
三个数相加,先把前两个数相加,再和第三个数相加;或者先把后两个数相加,再和第一个数相加,和不变。
乘法分配律
(
+b)
×c=
×c+b×c
两个数相加再乘另一个数,等于把这个数分别同两个加数相乘,再把两个积相加,得数不变。
字母
文字
用字母来表示运算律更简洁!
C
=
S
=
正方形的周长=
正方形的面积=
×
×4
边长×4
边长×边长
字母和数相乘
字母和字母相乘
C=
×4
×1
×b
S
=
×
乘号省略不写,数写在字母的前面
=4
=
不同字母相乘
相同字母相乘
=
b
=
?
读作:
的平方
(1)什么时候,字母式子可以简写?
(2)如何简写?
故事反馈:
正
正
×
②
b-c可以写成b·c,或bc。
(
)
①
×5可以写成
5。
(
)
③
c×c可以写成2c。
(
)
×
×
5
c?
800+x
x+y
1.
y-x
5
古希腊数学家:丢番图
每个价钱×4
jia
×4
法国数学家:韦达
现代代数学之父
1200年
每个重量×4
zhong
×4
×4
a×4
在今天看来,用字母表示数是一件简单的事情,但在数学发展史上,这项工作却耗费了数学家相当长的时间。
古时的埃及人和巴比伦人都是使用语言来表示数及数量关系。
用这三张牌,算出24。
第一关
用这四张牌,算出24。
第二关
用这四张牌,算出24。
第三关
J
Q
K
1
12
11
13
A
1
2
放入硬币/枚
出来硬币/枚
2
4
1
2
放入硬币/枚
出来硬币/枚
3
6
2
4
1
2
放入硬币/枚
出来硬币/枚
3
6
2
4
1
2
放入硬币/枚
出来硬币/枚
……
你能想办法把所有的情况都表示出来吗?
3
6
2
4
1
2
放入硬币/枚
出来硬币/枚
……
×2
1
4
放入硬币/枚
出来硬币/枚
2
5
1
4
放入硬币/枚
出来硬币/枚
3
6
2
5
1
4
放入硬币/枚
出来硬币/枚
3
6
2
5
1
4
放入硬币/枚
出来硬币/枚
……
你能想办法把所有的情况表示出来吗?
3
6
2
5
1
4
放入硬币/枚
出来硬币/枚
……
+3
一个含有字母的式子不仅能表示一个数量,还能表示一个数量关系。
回顾思考:
①字母可以表示怎样的数?
②含有字母的式子可以表示什么?
③用字母和含有字母的式子来表示有什么好处?
1、甲、乙两地之间的公路长280千米,一辆汽车从甲地开往乙地。(只列式不计算)
已经行驶了50千米,剩下的千米数是
280-50;
已经行驶了74.5千米,剩下的千米数是
280-74.5;
已经行驶了b千米,剩下的千米数是
280-b
。
剩下的路程=
全长-已经行驶的路程
280-b
=160
280-b
=80
(
×b)×c=
×(b×c)
三个数相乘,先把前两个数相乘,再和第三个数相乘;或者先把后两个数相乘,再和第一个数相乘,积不变。
乘法结合律
加法结合律
×b=b×
两个数相乘,交换两个乘数的位置,积不变。
加法交换律
+b=b+
两个数相加,交换两个乘加数的位置,和不变。
乘法交换律
(
+b)+c=
+(b+c)
三个数相加,先把前两个数相加,再和第三个数相加;或者先把后两个数相加,再和第一个数相加,和不变。
乘法结合律
(
×b)×c=
×(b×c)
三个数相加,先把前两个数相加,再和第三个数相加;或者先把后两个数相加,再和第一个数相加,和不变。
乘法分配律
(
+b)
×c=
×c+b×c
两个数相加再乘另一个数,等于把这个数分别同两个加数相乘,再把两个积相加,得数不变。
字母
文字
用字母来表示运算律更简洁!
C
=
S
=
正方形的周长=
正方形的面积=
×
×4
边长×4
边长×边长
字母和数相乘
字母和字母相乘
C=
×4
×1
×b
S
=
×
乘号省略不写,数写在字母的前面
=4
=
不同字母相乘
相同字母相乘
=
b
=
?
读作:
的平方
(1)什么时候,字母式子可以简写?
(2)如何简写?
故事反馈:
正
正
×
②
b-c可以写成b·c,或bc。
(
)
①
×5可以写成
5。
(
)
③
c×c可以写成2c。
(
)
×
×
5
c?
800+x
x+y
1.
y-x
5
古希腊数学家:丢番图
每个价钱×4
jia
×4
法国数学家:韦达
现代代数学之父
1200年
每个重量×4
zhong
×4
×4
a×4
在今天看来,用字母表示数是一件简单的事情,但在数学发展史上,这项工作却耗费了数学家相当长的时间。
古时的埃及人和巴比伦人都是使用语言来表示数及数量关系。
