人教版七年级上册数学4.3.3余角和补角课件(15张)
文档属性
| 名称 | 人教版七年级上册数学4.3.3余角和补角课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 344.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 10:52:15 | ||
图片预览


文档简介
主要内容:
余角的概念;
角的分类;
补角的概念;
习题讲解;
(和为90)
(和为180)
(锐角、直角、钝角)
比萨斜塔
重庆荣昌
舍利塔
(
(
1
2
(
(
1
2
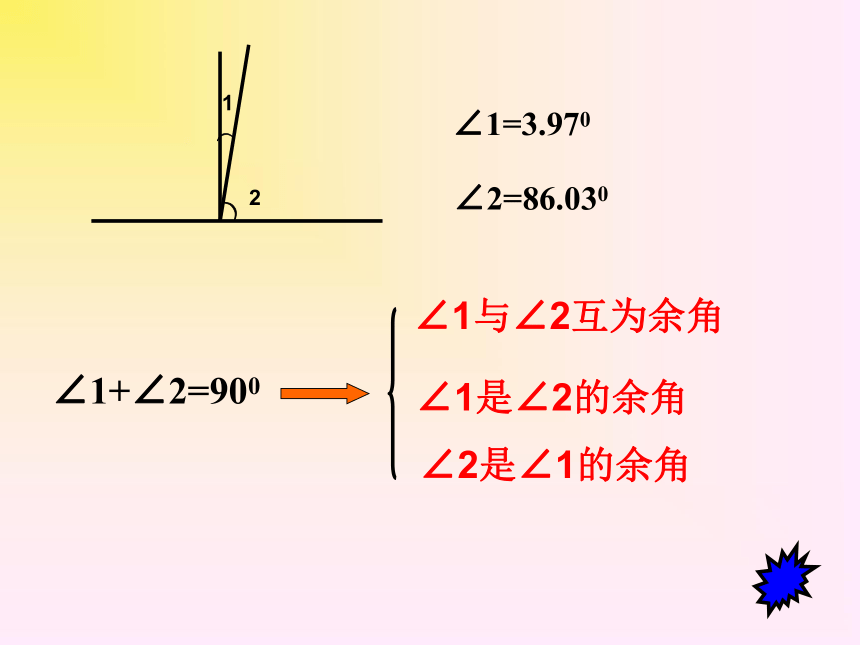
∠1=3.970
∠2=86.030
∠1+∠2=900
∠1与∠2互为余角
∠1是∠2的余角
∠2是∠1的余角
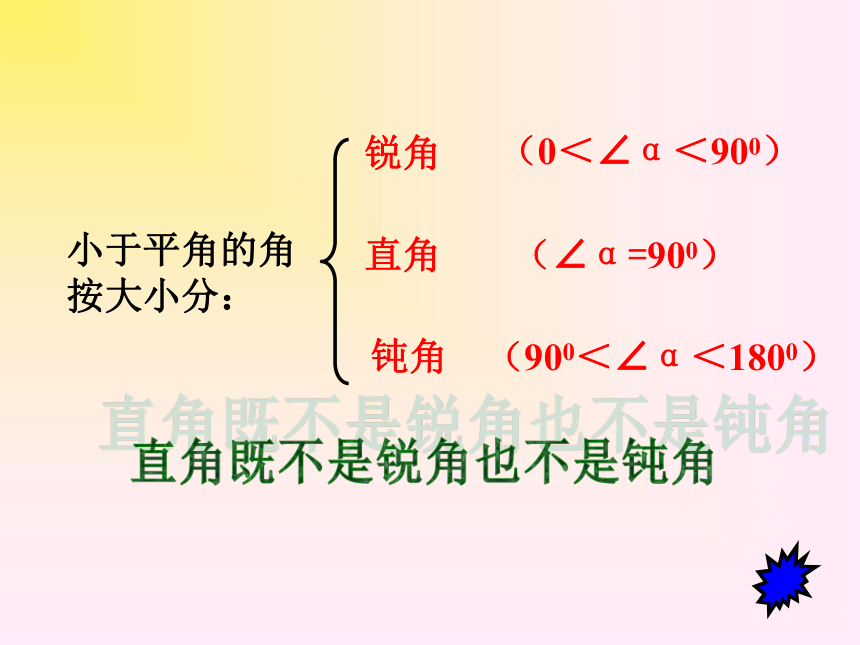
小于平角的角
按大小分:
锐角
直角
钝角
(0<∠α<900)
(∠α=900)
(900<∠α<1800)
(
(
1
2
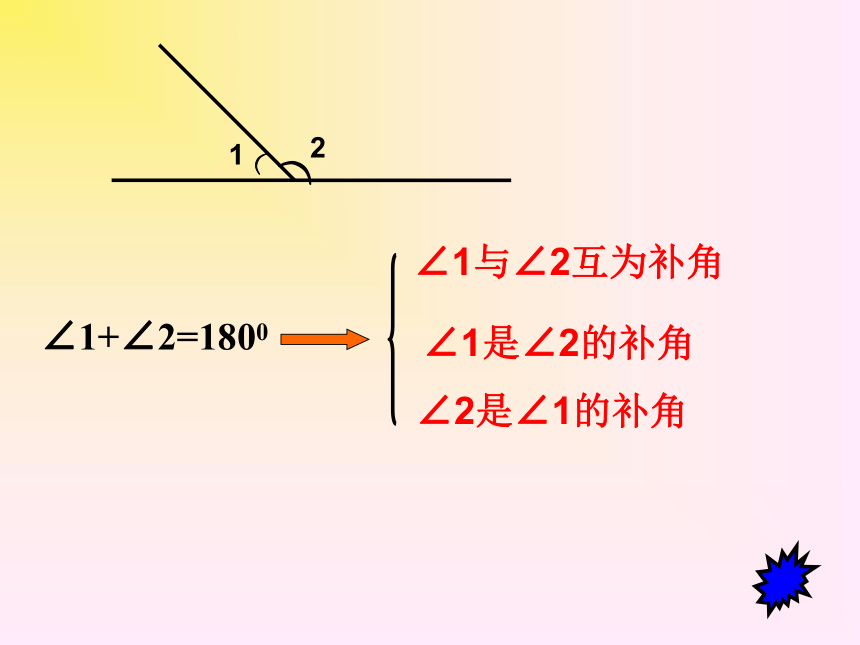
∠1+∠2=1800
∠1与∠2互为补角
∠1是∠2的补角
∠2是∠1的补角
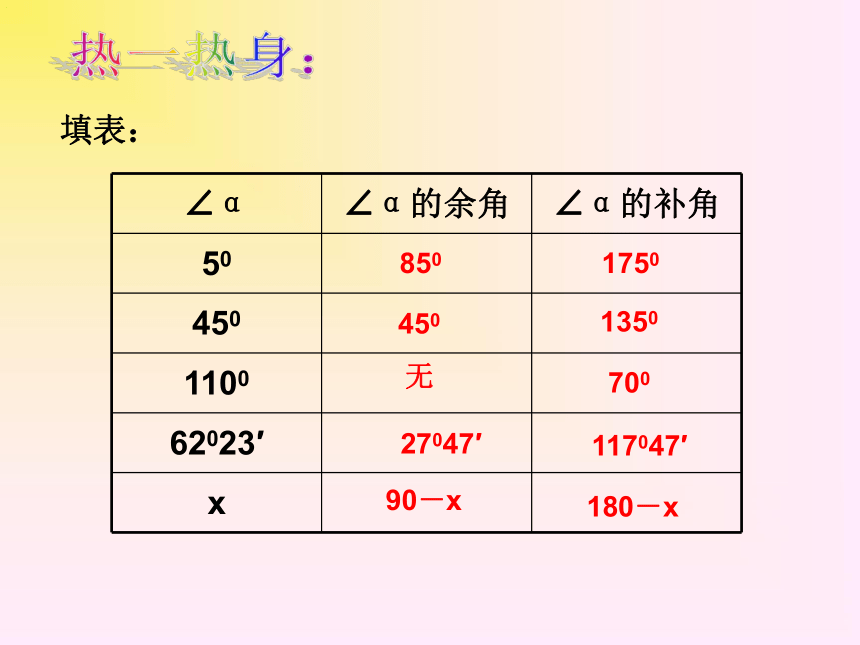
填表:
∠α
∠α的余角
∠α的补角
50
450
1100
62023′
x
850
1750
450
1350
无
700
27047′
117047′
90-x
180-x
例1、下列说法正确的有( )
①若两个角互补,则必定一个是锐角,
一个是钝角;
②一个角的补角一定大于这个角;
③若∠1+∠2=900,则∠1与∠2互为余角;
④若∠1+∠2+∠3=1800,
则∠1、∠2、∠3互为补角;
A 1个
B 2个
C 3个
D 4个
A
例2、一个角的补角是这个角的3倍,求这个角?
例3、若∠α与∠β互补,且∠α︰∠β=5︰4,
求这两个角?
例4、E、D、F三点共线,∠CDE=900,∠1=∠2,
(1)写出图中所有相等的角,选择一组等角写出证明过程程;
(2)写出图中所有互余的角;
(3)写出图中所有互补的角;
(
(
(
(
1
2
3
4
若∠1与∠2互余,∠2与∠3互余,
则∠___=∠____
若∠1与∠2互余,∠3与∠4互余,
且∠1=∠3,则∠____=∠____
1
3
2
4
若∠1与∠2互补,∠2与∠3互补,
则∠____=∠____
若∠1与∠2互补,∠3与∠4互补,
且∠1=∠3,则∠____=∠___
1
3
4
2
如图,已知:O是直线AB上一点,把直角三角板的直角顶点放在点O,此时三角板可绕着点O在直线AB上方旋转,请观察在运动过程中,∠AOC和∠BOD始终保持什么关系?为什么?
谢谢大家
余角的概念;
角的分类;
补角的概念;
习题讲解;
(和为90)
(和为180)
(锐角、直角、钝角)
比萨斜塔
重庆荣昌
舍利塔
(
(
1
2
(
(
1
2
∠1=3.970
∠2=86.030
∠1+∠2=900
∠1与∠2互为余角
∠1是∠2的余角
∠2是∠1的余角
小于平角的角
按大小分:
锐角
直角
钝角
(0<∠α<900)
(∠α=900)
(900<∠α<1800)
(
(
1
2
∠1+∠2=1800
∠1与∠2互为补角
∠1是∠2的补角
∠2是∠1的补角
填表:
∠α
∠α的余角
∠α的补角
50
450
1100
62023′
x
850
1750
450
1350
无
700
27047′
117047′
90-x
180-x
例1、下列说法正确的有( )
①若两个角互补,则必定一个是锐角,
一个是钝角;
②一个角的补角一定大于这个角;
③若∠1+∠2=900,则∠1与∠2互为余角;
④若∠1+∠2+∠3=1800,
则∠1、∠2、∠3互为补角;
A 1个
B 2个
C 3个
D 4个
A
例2、一个角的补角是这个角的3倍,求这个角?
例3、若∠α与∠β互补,且∠α︰∠β=5︰4,
求这两个角?
例4、E、D、F三点共线,∠CDE=900,∠1=∠2,
(1)写出图中所有相等的角,选择一组等角写出证明过程程;
(2)写出图中所有互余的角;
(3)写出图中所有互补的角;
(
(
(
(
1
2
3
4
若∠1与∠2互余,∠2与∠3互余,
则∠___=∠____
若∠1与∠2互余,∠3与∠4互余,
且∠1=∠3,则∠____=∠____
1
3
2
4
若∠1与∠2互补,∠2与∠3互补,
则∠____=∠____
若∠1与∠2互补,∠3与∠4互补,
且∠1=∠3,则∠____=∠___
1
3
4
2
如图,已知:O是直线AB上一点,把直角三角板的直角顶点放在点O,此时三角板可绕着点O在直线AB上方旋转,请观察在运动过程中,∠AOC和∠BOD始终保持什么关系?为什么?
谢谢大家
