七年级上册数学人教版3.3.1解一元一次方程二——去括号解一元一次方程课件(22张ppt)
文档属性
| 名称 | 七年级上册数学人教版3.3.1解一元一次方程二——去括号解一元一次方程课件(22张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 11:04:06 | ||
图片预览








文档简介
3.3 解一元一次方程
去括号与去分母(一)
学习目标
1.掌握用一元一次方程解决实际问题的方法,会分配律,去括号解决关于含括号的一元一次方程。
2.经历应用方程解决实际问题的过程,发展分析问题,解决问题能力,进一步体会方程模型的作用。
3.关注学生在建立方程和解方程过程中的表现,发展学生积极思考的学习态度以及合作交流的意识。
温故知新
1、一元一次方程的解法我们学习了几步?
移项 合并同类项 系数化为1
2、移项,合并同类项,系数化为1,要注意什么?
1移项时要变号。(变成相反数)
2合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变。
3系数化为1,也就是说方程两边同时除以未知数前面的系数。
知识讲解
我们在方程6x-7=4x-1后加上一个括号得
6x-7=4(x-1)会解吗?
在前面再加上一个负号呢? 6x-7=-4(x-1)
问题1:某工厂加强节能措施,去年下半年与上半年
相比,月平均用电量减少2 000 kW·h(千瓦·时),
全年用电15 万 kW·h.这个工厂去年上半年每月平均
用电是多少?
温馨提示:1 kW·h的电量是指1 kW的电器1 h的用电量.
思考:
1.题目中涉及了哪些量?
2.题目中的相等关系是什么?
月平均用电量×n(月数)=n个月用电量
上半年的用电量+下半年的用电量=全年的用电量
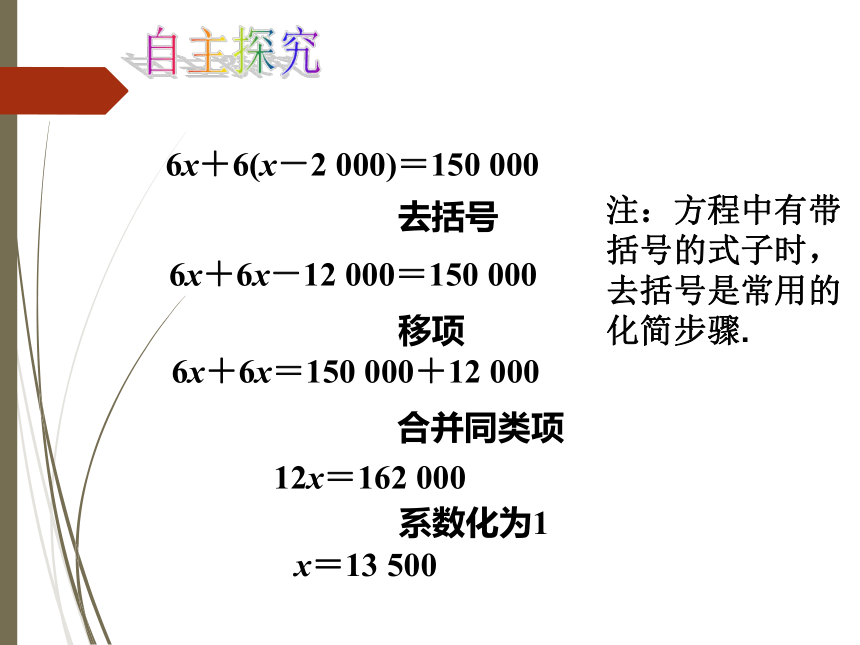
6x+6(x -2 000)=150 000
分析:
设上半年每月平均用电量列出方程xkW·h,
则下半年每月平均用电为(x-2000) kW·h.
上半年共用电为:6x kW·h;
上半年共用电为:6(x-2000) kW·h.
根据题意列出方程
怎样解这个方程?
这个方程与我们前面研究过的方程有什么不同?
怎样使方程向x=a的形式转化?
去括号法则:
(1)括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变符号。
(2)括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
x=13 500
去括号
合并同类项
移项
6x+6x=150 000+12 000
系数化为1
12x=162 000
注:方程中有带
括号的式子时,去括号是常用的化简步骤.
思考:
本题还有其他列方程的方法吗?
用其他方法列出的方程应怎样解?
设上半年平均每月用电x度
列方程
通过以上解方程的过程,你能总结出含有
括号的一元一次方程解法的一般步骤吗?
去括号
移项
合并同类项
系数化为1
例1 解下列方程:
(1)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(2)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
期中数学考试后,小明、小方和小华三名同学对答案,其中有一道题三人答案各不相同,每个人都认为自己做得对,你能帮他们看看到底谁做得对吗?做错的同学又是错在哪儿呢?
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能算出x是几吗?
去括号错
移项错
小方:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
移项错
小华:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能算出x是几吗?
列方程错
小明:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能算出x是几吗?
例2 一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的平均速度.
思考:
1、问题中涉及到顺、逆流因素,这类问题中有哪
些基本相等关系?
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
2.一般情况下可以认为这艘船往返的路程相等,
则顺流速度___顺流时间___逆流速度 ___逆流时间
解:设船在静水中的平均速度为x km/h,则顺流
的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据往返路程相等,列出方程,得
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
一架飞机在两城之间航行,风速为24 km/h,顺风
飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,
则在顺风中的速度为(x+24) km/h ,
在逆风中的速度为(x-24) km/h.
根据题意,得
解得
两城市的距离:
答:两城市之间的距离为2 448 km.
1.本节课你有哪些收获?
2.你觉得自己掌握这些知识困难吗?
3.在解决问题时应该注意些什么呢?
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
去括号与去分母(一)
学习目标
1.掌握用一元一次方程解决实际问题的方法,会分配律,去括号解决关于含括号的一元一次方程。
2.经历应用方程解决实际问题的过程,发展分析问题,解决问题能力,进一步体会方程模型的作用。
3.关注学生在建立方程和解方程过程中的表现,发展学生积极思考的学习态度以及合作交流的意识。
温故知新
1、一元一次方程的解法我们学习了几步?
移项 合并同类项 系数化为1
2、移项,合并同类项,系数化为1,要注意什么?
1移项时要变号。(变成相反数)
2合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变。
3系数化为1,也就是说方程两边同时除以未知数前面的系数。
知识讲解
我们在方程6x-7=4x-1后加上一个括号得
6x-7=4(x-1)会解吗?
在前面再加上一个负号呢? 6x-7=-4(x-1)
问题1:某工厂加强节能措施,去年下半年与上半年
相比,月平均用电量减少2 000 kW·h(千瓦·时),
全年用电15 万 kW·h.这个工厂去年上半年每月平均
用电是多少?
温馨提示:1 kW·h的电量是指1 kW的电器1 h的用电量.
思考:
1.题目中涉及了哪些量?
2.题目中的相等关系是什么?
月平均用电量×n(月数)=n个月用电量
上半年的用电量+下半年的用电量=全年的用电量
6x+6(x -2 000)=150 000
分析:
设上半年每月平均用电量列出方程xkW·h,
则下半年每月平均用电为(x-2000) kW·h.
上半年共用电为:6x kW·h;
上半年共用电为:6(x-2000) kW·h.
根据题意列出方程
怎样解这个方程?
这个方程与我们前面研究过的方程有什么不同?
怎样使方程向x=a的形式转化?
去括号法则:
(1)括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变符号。
(2)括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
x=13 500
去括号
合并同类项
移项
6x+6x=150 000+12 000
系数化为1
12x=162 000
注:方程中有带
括号的式子时,去括号是常用的化简步骤.
思考:
本题还有其他列方程的方法吗?
用其他方法列出的方程应怎样解?
设上半年平均每月用电x度
列方程
通过以上解方程的过程,你能总结出含有
括号的一元一次方程解法的一般步骤吗?
去括号
移项
合并同类项
系数化为1
例1 解下列方程:
(1)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(2)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
期中数学考试后,小明、小方和小华三名同学对答案,其中有一道题三人答案各不相同,每个人都认为自己做得对,你能帮他们看看到底谁做得对吗?做错的同学又是错在哪儿呢?
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能算出x是几吗?
去括号错
移项错
小方:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
移项错
小华:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能算出x是几吗?
列方程错
小明:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能算出x是几吗?
例2 一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的平均速度.
思考:
1、问题中涉及到顺、逆流因素,这类问题中有哪
些基本相等关系?
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
2.一般情况下可以认为这艘船往返的路程相等,
则顺流速度___顺流时间___逆流速度 ___逆流时间
解:设船在静水中的平均速度为x km/h,则顺流
的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据往返路程相等,列出方程,得
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
一架飞机在两城之间航行,风速为24 km/h,顺风
飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,
则在顺风中的速度为(x+24) km/h ,
在逆风中的速度为(x-24) km/h.
根据题意,得
解得
两城市的距离:
答:两城市之间的距离为2 448 km.
1.本节课你有哪些收获?
2.你觉得自己掌握这些知识困难吗?
3.在解决问题时应该注意些什么呢?
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
