鲁科版(2019)高中物理 选择性必修第一册 第2章 第5节 生活中的振动学案(含练习)
文档属性
| 名称 | 鲁科版(2019)高中物理 选择性必修第一册 第2章 第5节 生活中的振动学案(含练习) | 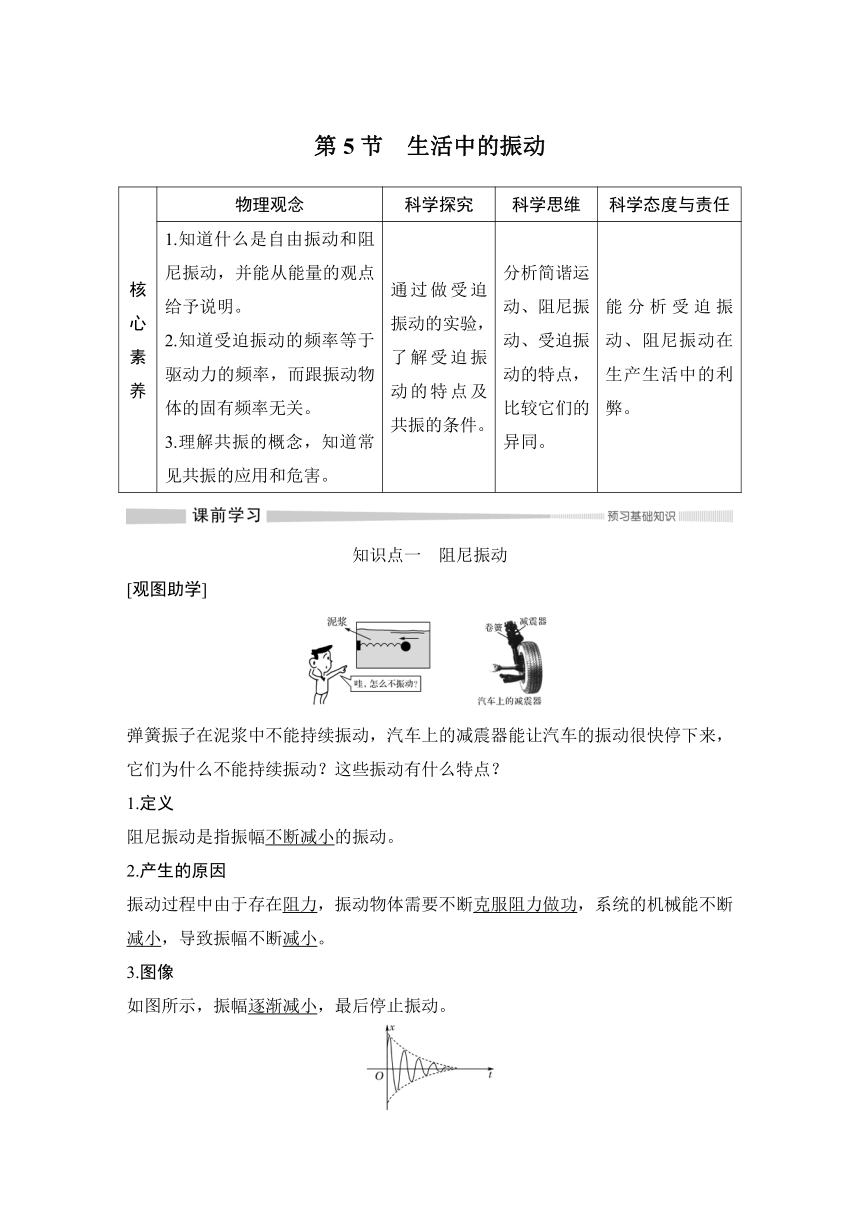 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-05 21:04:42 | ||
图片预览





文档简介
第5节 生活中的振动
核心素养 物理观念 科学探究 科学思维 科学态度与责任
1.知道什么是自由振动和阻尼振动,并能从能量的观点给予说明。
2.知道受迫振动的频率等于驱动力的频率,而跟振动物体的固有频率无关。
3.理解共振的概念,知道常见共振的应用和危害。 通过做受迫振动的实验,了解受迫振动的特点及共振的条件。 分析简谐运动、阻尼振动、受迫振动的特点,比较它们的异同。 能分析受迫振动、阻尼振动在生产生活中的利弊。
知识点一 阻尼振动
[观图助学]
弹簧振子在泥浆中不能持续振动,汽车上的减震器能让汽车的振动很快停下来,它们为什么不能持续振动?这些振动有什么特点?
1.定义
阻尼振动是指振幅不断减小的振动。
2.产生的原因
振动过程中由于存在阻力,振动物体需要不断克服阻力做功,系统的机械能不断减小,导致振幅不断减小。
3.图像
如图所示,振幅逐渐减小,最后停止振动。
[思考判断]
(1)做阻尼振动的物体因克服阻力做功,它的机械能逐渐减小。(√)
(2)阻力越大,物体的振幅减小的越快。(√)
(3)阻尼振动振幅逐渐减小时,其固有频率也逐渐减小。(×)
泥浆中的弹簧振子、汽车上的减震器之所以不能持续的振动,是因为它们在振动过程中受到阻力,使振动逐渐减弱。
被敲击的锣做阻尼振动,发出的声音逐渐减弱。
知识点二 受迫振动与共振 共振的应用与防止
[观图助学]
1.受迫振动
(1)驱动力:为了获得稳定的振动,通常需要给振动物体施加一个周期性的外力,这种周期性的外力称为驱动力。
(2)受迫振动:在周期性外力作用下的振动。
(3)受迫振动的周期或频率
物体做受迫振动时,振动稳定后的周期(或频率)总等于驱动力的周期(或频率),与物体的固有周期(或固有频率)无关。
2.共振
(1)条件:驱动力的周期(或频率)等于物体的固有周期(或固有频率)。
(2)特征:共振时,物体振动的振幅最大。
(3)共振曲线:如图所示。
3.共振的应用与防止
(1)共振的应用
在应用共振时,应使驱动力频率接近或等于振动系统的固有频率,振动将更剧烈。如路面共振破碎机、音叉共鸣箱。
(2)共振的防止
在防止共振时,驱动力频率与系统的固有频率相差越大越好。如集体列队经过桥梁时要便步走。
[思考判断]
(1)做受迫振动的物体其频率由自身决定。(×)
(2)驱动力的频率越大振动物体振幅越大(×)
(3)共振的条件是驱动力的频率等于物体的固有频率。(√)
稳定的振动是在周期性驱动力的作用下振幅和频率都不变的振动,不能理解为简谐运动。
驱动力的频率f越接近振动系统的固有频率f固,受迫振动的振幅越大,反之振幅越小。
吉他琴弦的声音很小,几乎听不见,但是弦被安装在谐振器体上后,弦乐的声音就会被放大,这利用了共振。
核心要点 对阻尼振动的理解
[要点归纳]
振动类型 简谐运动 阻尼振动
产生条件 不受阻力作用 受阻力作用
频率 固有频率 频率不变
振幅 不变 减小
振动图像
实例 弹簧振子振动,单摆做小角度摆动 敲锣打鼓发出的声音越来越弱
[试题案例]
[例1] (多选)一单摆做阻尼振动,则在振动过程中( )
A.振幅越来越小,周期也越来越小
B.振幅越来越小,周期不变
C.在振动过程中,通过某一位置时,机械能始终不变
D.在振动过程中,机械能不守恒,周期不变
解析 因单摆做阻尼振动,所以振幅越来越小,机械能越来越小,振动周期不变。
答案 BD
规律总结 阻尼振动的能量和周期
(1)阻尼振动的振幅不断减小,能量不断减少,但阻尼振动的频率不变,其频率为固有频率,由系统本身决定。
(2)自由振动是一种理想情况,也叫简谐运动。实际中的振动都会受到阻力的作用,当阻力较小时,可认为是简谐运动。
(3)阻尼振动中,机械能E等于动能Ek和势能Ep之和,即E=Ek+Ep,E减小,但动能和势能相互转化,当Ep相等时,Ek不相等。
[针对训练1] (多选)如图所示是单摆做阻尼振动的振动图线,下列说法中正确的是( )
A.摆球A时刻的动能等于B时刻的动能
B.摆球A时刻的势能等于B时刻的势能
C.摆球A时刻的机械能等于B时刻的机械能
D.摆球A时刻的机械能大于B时刻的机械能
解析 在单摆振动过程中,因不断克服空气阻力做功使振动的能量逐渐转化为内能,C错误,D正确;虽然单摆总的机械能在逐渐减小,但在振动过程中动能和势能仍不断地相互转化。由于A、B两时刻单摆的位移相等,所以势能相等,但动能不相等,A错误,B正确。
答案 BD
核心要点 对受迫振动与共振的理解
[问题探究]
双桶洗衣机在衣服脱水完毕拔掉电源后,电动机还要转动一会才能停下来。在拔掉电源后,发现洗衣机先振动得比较弱,有一阵子振动得很剧烈,然后振动慢慢减弱直至停下来。
(1)开始时,洗衣机为什么振动比较弱?
(2)期间剧烈振动的原因是什么?
答案 (1)开始时,脱水桶转动的频率远高于洗衣机的固有频率,振幅较小,振动比较弱。
(2)当洗衣机脱水桶转动的频率等于洗衣机的固有频率时发生共振,振动剧烈。
[探究归纳]
自由振动、受迫振动、共振的比较
自由振动 受迫振动 共振
振动原因 受回复力 受周期性驱动力作用 受周期性驱动力作用
振动周期或频率 由物体本身性质决定,即固有周期或固有频率 由驱动力的周期或频率决定,即T=T驱或f=f驱 T驱=T固或f驱=f固
振动能量 振动物体的机械能不变 由产生驱动力的物体提供 振动物体获得的能量最大
常见例子 弹簧振子或单摆 扬声器纸盆的振动 路面共振破碎机、音叉共鸣箱
[试题案例]
[例2] 如图所示,在一条张紧的绳上挂7个摆,先让A摆振动起来,则其余各摆也随之振动。已知A、B、F三摆的摆长相同,则下列判断正确的是( )
A.7个摆的固有频率都相同
B.振动稳定后7个摆的振动频率各不相同
C.B、F摆的摆长与A摆相同,它们的振幅最大
D.除A摆外,D、E摆离A摆最近,它们的振幅最大
解析 7个摆的摆长不完全相同,固有频率不完全相同,选项A错误;A摆振动起来后,带动其余6个摆做受迫振动,振动稳定后7个摆的振动频率都相同,选项B错误;B、F摆的摆长与A摆相同,发生共振,选项C正确,D错误。
答案 C
[针对训练2] 一个单摆做受迫振动,其共振曲线(振幅A与驱动力的频率f的关系)如图所示,则( )
A.此单摆的固有周期约为0.5 s
B.此单摆的摆长约为1 m
C.若摆长增大,单摆的固有频率增大
D.若摆长增大,共振曲线的峰将向右移动
解析 由共振条件知单摆的固有频率为f=0.5 Hz,则其固有周期为T==2 s,选项A错误;由单摆周期公式T=2π,可求得单摆摆长为l=≈1 m,选项B正确;摆长增大,单摆的固有周期变大,其固有频率变小,共振曲线的峰将向左移动,选项C、D错误。
答案 B
1.(对阻尼振动的理解)(多选)一单摆在空气中振动,振幅逐渐减小,下列说法正确的是( )
A.振动的机械能逐渐转化为其他形式的能
B.后一时刻的动能一定小于前一时刻的动能
C.后一时刻的势能一定小于前一时刻的势能
D.后一时刻的机械能一定小于前一时刻的机械能
解析 单摆振动过程中,会不断克服空气阻力做功使机械能逐渐减小,A、D正确;虽然单摆总的机械能在逐渐减小,但在振动过程中动能和势能仍不断地相互转化。动能转化为势能时,动能逐渐减少,势能逐渐增加,而势能转化为动能时,势能逐渐减少,动能逐渐增加,所以不能断言后一时刻的动能(或势能)一定小于前一时刻的动能(或势能),故B、C错误。
答案 AD
2.(对受迫振动的理解)如图所示的装置,弹簧振子的固有频率是4 Hz。现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为1 Hz,则把手转动的频率为( )
A.1 Hz B.3 Hz
C.4 Hz D.5 Hz
解析 因把手每转动一周,驱动力完成一次周期性变化,即把手转动频率即为驱动力的频率。弹簧振子做受迫振动,而受迫振动的频率等于驱动力的频率,与振动系统的固有频率无关,故A正确。
答案 A
3.(受迫振动、共振)(多选)如图所示,在一根张紧的水平绳上悬挂五个摆,其中A、E的摆长为l,B的摆长为0.5l,C的摆长为1.5l,D的摆长为2l,先使A振动起来,其他各摆随后也振动起来,则摆球振动稳定后( )
A.D的振幅一定最大 B.E的振幅一定最大
C.B的周期一定最短 D.其余四个摆的周期相同
解析 A振动起来后,使得B、C、D、E做受迫振动,振动的频率都等于A振动的频率,即各摆振动的周期都相等,选项C错误,D正确;由于D与A的摆长相差最大,E与A的摆长相等,所以D的振幅最小,E发生共振,振幅最大,选项A错误,B正确。
答案 BD
4.(共振的防止和利用)(多选)下列关于共振和防止共振的说法,正确的是( )
A.共振现象总是有害的,所以要避免共振现象发生
B.队伍过桥要慢行是为了不产生周期性的驱动力,从而避免产生共振
C.火车过桥慢行是为了使驱动力的频率远小于桥的固有频率,从而避免产生共振
D.利用共振时,应使驱动力的频率接近或等于振动物体的固有频率;防止共振危害时,应使驱动力的频率远离振动物体的固有频率
解析 共振现象不一定总是有害的,有的时候我们要利用共振现象,如共振筛,共振转速计等,故A错误;队伍过桥慢行也会产生周期性的驱动力,即会产生共振,故B错误;火车过桥要慢行,目的是使驱动力频率远小于桥梁的固有频率,以免发生共振损坏桥,C正确;受迫振动的频率等于驱动力的频率,所以利用共振时,应使驱动力的频率接近或等于振动物体的固有频率,防止共振危害时,应尽量使驱动力频率远离振动物体的固有频率,故D正确。
答案 CD
基础过关
1.自由摆动的秋千,摆动的振幅越来越小,下列说法正确的是( )
A.机械能守恒
B.能量正在消失
C.总能量守恒,机械能减小
D.只有动能和势能的相互转化
解析 秋千摆动时受到空气的阻力,秋千的机械能向其他形式的能转化,但总的能量守恒。
答案 C
2.(多选)对于阻尼振动,下列说法正确的是( )
A.阻尼振动就是减幅振动,其振动的能量不断减少
B.实际的振动系统不可避免地要受到阻尼作用
C.阻尼振动的振幅、振动能量、振动周期逐渐减小
D.对做阻尼振动的振子来说,其机械能逐渐转化为内能
解析 振动系统的振动频率与本身的结构有关,为固有频率,所以在阻尼振动中,振幅减小,振动能量减少,最终转化为内能,但周期不变,故A、D正确,C错误;实际的振动系统都要受到摩擦或空气阻力等阻尼作用,故B正确。
答案 ABD
3.下列振动中属于受迫振动的是( )
A.用重锤敲击一下悬吊着的钟后,钟的摆动
B.打点计时器接通电源后,振针的振动
C.小孩睡在自由摆动的吊床上,小孩随着吊床一起摆动
D.弹簧振子在竖直方向上上下振动
解析 受迫振动是振动物体在驱动力作用下的运动,故只有B正确。
答案 B
4.在飞机的发展史中有一个阶段,飞机上天后不久,飞机的机翼(翅膀)很快就抖动起来,而且越抖越厉害。后来经过人们的探索,利用在飞机机翼前缘处装置一个配重杆的方法,解决了这一问题。在飞机机翼前装置配重杆的目的主要是( )
A.加大飞机的惯性 B.使机体更加平衡
C.使机翼更加牢固 D.改变机翼的固有频率
解析 飞机的机翼(翅膀)很快就抖动起来,是因为驱动力的频率接近机翼的固有频率发生共振,在飞机机翼前装置配重杆,是为了改变机翼的固有频率,使驱动力的频率远离机翼的固有频率。故A、B、C错误,D正确。
答案 D
5.部队经过桥梁时,规定不许齐步走,登山运动员登高山时,不许高声叫喊,主要原因是( )
A.减轻对桥的压力,避免产生回声
B.减少对桥、雪山的冲量
C.避免使桥、雪山发生共振
D.使桥受到的压力更不均匀,使登山运动员耗散能量减少
解析 部队过桥时若齐步走会给桥梁施加周期性外力,容易使桥的振动幅度增加,即发生共振,造成桥梁倒塌;登山运动员登高山时高声叫喊,声波容易引发雪山共振而发生雪崩,故选项C正确。
答案 C
6.如图所示是单摆做阻尼振动的位移—时间图线,下列说法中正确的是( )
A.摆球在P与N时刻的势能相等
B.摆球在P与N时刻的动能相等
C.摆球在P与N时刻的机械能相等
D.摆球在P时刻的机械能小于在N时刻的机械能
解析 由于摆球的势能大小由其位移和摆球质量共同决定,P、N两时刻位移大小相同,所以势能相等,A正确;由于系统机械能在减少,P、N两时刻势能相同,则P时刻动能大于N时刻动能,B、C、D错误。
答案 A
7.任何物体都有自己的固有频率。研究表明,如果把人作为一个整体来看,在水平方向上振动时的固有频率约为5 Hz。当工人操作风镐、风铲、铆钉机等振动机械时,操作者在水平方向将做受迫振动。在这种情况下,下列说法正确的是( )
A.操作者的实际振动频率等于他自身的固有频率
B.操作者的实际振动频率等于机械的振动频率
C.为了保证操作者的安全,振动机械的频率应尽量接近人的固有频率
D.为了保证操作者的安全,应尽量提高操作者的固有频率
解析 物体在周期性驱动力作用下做受迫振动,受迫振动的频率等于驱动力的频率,与固有频率无关,可知操作者的实际频率等于机械的振动频率,故A错误,B正确;当驱动力频率等于物体的固有频率时,物体的振幅最大,产生共振现象,所以为了保证操作者的安全,振动机械的频率应尽量远离人的固有频率,操作者的固有频率无法提高,故C、D错误。
答案 B
8.如图所示,三个单摆的摆长分别为l1=1.5 m,l2=1 m,l3=0.5 m,现用一周期等于2 s的驱动力,使它们做受迫振动,那么当它们的振动稳定时,下列判断中正确的是( )
A.三个摆的周期和振幅相等
B.三个摆的周期不等,振幅相等
C.三个摆的周期相等,但振幅不等
D.三个摆的周期和振幅都不相等
解析 三个摆的振动都是受迫振动,所以振动的频率都与驱动力的频率相同,三者的频率相同。由f==知,2的固有频率与驱动力的频率最接近,振幅最大,而1和3的振幅较小,故C正确。
答案 C
9.在实验室可以做“声波碎杯”的实验。用手指轻弹一只酒杯,可以听到清脆的声音,测得该声音的频率为500 Hz。将这只酒杯放在两个大功率的声波发生器之间,操作人员通过调整其发出的声波,就能使酒杯碎掉(如图所示)。下列说法正确的是( )
A.操作人员一定是把声波发生器的功率调到很大
B.操作人员可能是使声波发生器发出了频率很高的超声波
C.操作人员一定是同时增大了声波发生器发出声波的频率和功率
D.操作人员只需将声波发生器发出的声波频率调到500 Hz
解析 驱动力的频率与系统的固有频率相等时,受迫振动的振幅最大,形成共振。操作人员只需将声波发生器发出的声波频率调到500 Hz,就能使酒杯碎掉,D正确。
答案 D
能力提升
10.(多选)铺设铁轨时,每两根钢轨接缝处都必须留有一定的间隙,匀速运行的列车经过轨端接缝处时,车轮就会受到一次冲击。由于每一根钢轨长度相等。所以这个冲击力是周期性的,列车受到周期性的冲击做受迫振动。普通钢轨长为
12.6 m,列车固有振动周期为0.315 s。下列说法正确的是( )
A.列车的危险速率为40 m/s
B.列车过桥需要减速,是为了防止发生共振现象
C.列车运行的振动频率和列车的固有频率总是相等的
D.增加钢轨的长度有利于列车高速运行
解析 对于受迫振动,当驱动力的频率与固有频率相等时将发生共振现象,所以列车的危险速率v==40 m/s,A正确;为了防止共振现象发生,列车过桥需要减速,B正确;列车运行的振动频率等于做受迫振动的驱动力的频率,与列车的固有频率无关,C项错;由v=知L增大时,T不变,v变大,D正确。
答案 ABD
11.(多选)蜘蛛虽有8只眼睛,但视力很差,完全靠感觉来捕食和生活,它的腿能敏捷地感觉到落在丝网上的昆虫对丝网造成的振动。当丝网的振动频率为f=
200 Hz左右时,丝网振动的振幅最大,最大振幅为0.5 cm。已知该丝网共振时,蜘蛛能立即捕捉到丝网上的昆虫。则对于落在丝网上的昆虫( )
A.当其翅膀振动的频率为200 Hz左右时,蜘蛛能立即捕捉到它
B.当其翅膀振动的周期为0.05 s左右时,蜘蛛能立即捕捉到它
C.当其翅膀振动的频率为300 Hz左右时,蜘蛛能立即捕捉到它
D.当其翅膀振动的频率为250 Hz时,该丝网的振幅一定小于0.5 cm
解析 当昆虫翅膀振动的频率与丝网的振动频率相等时,即翅膀振动的频率f′=f=200 Hz时,发生共振,蜘蛛能立即捕捉到昆虫,故A正确,C错误;根据周期与频率之间的关系得:T== s=0.005 s,即当昆虫翅膀振动的周期为0.005 s左右时,蜘蛛能立即捕捉到它,故B错误;当昆虫翅膀振动的频率为250 Hz左右时,没有发生共振,故该丝网的振幅小于0.5 cm,故D正确。
答案 AD
12.(多选)如图所示为两个单摆做受迫振动的共振曲线,则下列说法正确的是( )
A.两个单摆的固有周期之比为TⅠ∶TⅡ=5∶2
B.若两个受迫振动在地球上同一地点进行,则两个摆长之比为lⅠ∶lⅡ=4∶25
C.图线Ⅱ若是在地面上完成的,则该摆摆长约为1 m
D.若两个受迫振动分别在月球上和地球上进行,且摆长相等,则图线Ⅱ是月球上的单摆的共振曲线
解析 由共振曲线及共振的条件可知,Ⅰ和Ⅱ的固有频率分别为0.2 Hz和0.5 Hz,周期之比TⅠ∶TⅡ=5∶2,A正确;由单摆的周期公式T=2π可知,lⅠ∶lⅡ=T∶T=25∶4,B错误;同时可知lⅡ≈g,4π2)≈1 m,C正确;当摆长相等时,重力加速度越大,频率越大,月球表面重力加速度小于地球表面重力加速度,故D错误。
答案 AC
13.(多选)把一个筛子用四根弹簧支起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛(如图所示)。不开电动机让这个筛子自由振动时,完成20次全振动用15 s;在某电压下,电动偏心轮的转速是88 r/min。已知增大电动偏心轮的电压可以使其转速提高,而增加筛子的总质量可以增大筛子的固有周期。为使共振筛的振幅增大,以下做法可行的是( )
A.降低输入电压 B.提高输入电压
C.增加筛子质量 D.减小筛子质量
解析 筛子的固有频率为f固= Hz= Hz,而当时的驱动力频率为f驱= Hz= Hz,即f固答案 AD
14.如图所示,曲轴上悬挂一弹簧振子,转动摇把,曲轴可以带动弹簧振子上下振动。
(1)开始时不转动摇把,而用手往下拉振子,然后放手让振子上下振动,测得振子在10 s内完成20次振动,不考虑摩擦力和空气阻力,振子做什么振动?其固有周期和固有频率各是多少?若考虑摩擦力和空气阻力,振子做什么振动?
(2)在振子正常振动过程中,以转速4 r/s匀速转动把手,振子的振动稳定后,振子做什么运动?其周期是多少?
解析 (1)用手往下拉振子,放手后,因振子所受回复力满足F=-kx,所以做简谐运动,根据题意T固== s=0.5 s。f固== Hz=2 Hz,由于摩擦力和空气阻力的存在,振子克服摩擦力和阻力做功消耗能量,使其振幅越来越小,故振动为阻尼振动。
(2)由于把手转动的转速为4 r/s,它给弹簧振子的驱动力频率为f驱=4 Hz,周期T驱=0.25 s,故振子做受迫振动.振动达稳定状态后,其频率(或周期)等于驱动力的频率(或周期),而跟固有频率(或周期)无关。即f=f驱=4 Hz,T=T驱=0.25 s。
答案 (1)简谐运动 0.5 s 2 Hz 阻尼振动
(2)受迫振动 0.25 s
15.火车在轨道上行驶时,由于在钢轨接头处车轮受到撞击而上下振动。如果防震弹簧每受104 N的力将被压缩20 mm,而每根弹簧的实际负荷为5 000 kg,已知弹簧的振动周期T=2π,设钢轨长为12.5 m,问车速为多大时,火车振动得最剧烈?
解析 由题意可知弹簧在做受迫振动,弹簧发生共振时,振动最强烈,此时必须满足:f驱=f固(或T驱=T固)。
根据题意知,防震弹簧的劲度系数为
k== N/m=5×105 N/m
由于每根弹簧的实际负荷为m=5 000 kg,
所以弹簧的固有周期为
T固=2π=2π s= s
当振动最强烈时有T驱=== s
故火车的速度为v≈19.9 m/s。
答案 19.9 m/s
核心素养 物理观念 科学探究 科学思维 科学态度与责任
1.知道什么是自由振动和阻尼振动,并能从能量的观点给予说明。
2.知道受迫振动的频率等于驱动力的频率,而跟振动物体的固有频率无关。
3.理解共振的概念,知道常见共振的应用和危害。 通过做受迫振动的实验,了解受迫振动的特点及共振的条件。 分析简谐运动、阻尼振动、受迫振动的特点,比较它们的异同。 能分析受迫振动、阻尼振动在生产生活中的利弊。
知识点一 阻尼振动
[观图助学]
弹簧振子在泥浆中不能持续振动,汽车上的减震器能让汽车的振动很快停下来,它们为什么不能持续振动?这些振动有什么特点?
1.定义
阻尼振动是指振幅不断减小的振动。
2.产生的原因
振动过程中由于存在阻力,振动物体需要不断克服阻力做功,系统的机械能不断减小,导致振幅不断减小。
3.图像
如图所示,振幅逐渐减小,最后停止振动。
[思考判断]
(1)做阻尼振动的物体因克服阻力做功,它的机械能逐渐减小。(√)
(2)阻力越大,物体的振幅减小的越快。(√)
(3)阻尼振动振幅逐渐减小时,其固有频率也逐渐减小。(×)
泥浆中的弹簧振子、汽车上的减震器之所以不能持续的振动,是因为它们在振动过程中受到阻力,使振动逐渐减弱。
被敲击的锣做阻尼振动,发出的声音逐渐减弱。
知识点二 受迫振动与共振 共振的应用与防止
[观图助学]
1.受迫振动
(1)驱动力:为了获得稳定的振动,通常需要给振动物体施加一个周期性的外力,这种周期性的外力称为驱动力。
(2)受迫振动:在周期性外力作用下的振动。
(3)受迫振动的周期或频率
物体做受迫振动时,振动稳定后的周期(或频率)总等于驱动力的周期(或频率),与物体的固有周期(或固有频率)无关。
2.共振
(1)条件:驱动力的周期(或频率)等于物体的固有周期(或固有频率)。
(2)特征:共振时,物体振动的振幅最大。
(3)共振曲线:如图所示。
3.共振的应用与防止
(1)共振的应用
在应用共振时,应使驱动力频率接近或等于振动系统的固有频率,振动将更剧烈。如路面共振破碎机、音叉共鸣箱。
(2)共振的防止
在防止共振时,驱动力频率与系统的固有频率相差越大越好。如集体列队经过桥梁时要便步走。
[思考判断]
(1)做受迫振动的物体其频率由自身决定。(×)
(2)驱动力的频率越大振动物体振幅越大(×)
(3)共振的条件是驱动力的频率等于物体的固有频率。(√)
稳定的振动是在周期性驱动力的作用下振幅和频率都不变的振动,不能理解为简谐运动。
驱动力的频率f越接近振动系统的固有频率f固,受迫振动的振幅越大,反之振幅越小。
吉他琴弦的声音很小,几乎听不见,但是弦被安装在谐振器体上后,弦乐的声音就会被放大,这利用了共振。
核心要点 对阻尼振动的理解
[要点归纳]
振动类型 简谐运动 阻尼振动
产生条件 不受阻力作用 受阻力作用
频率 固有频率 频率不变
振幅 不变 减小
振动图像
实例 弹簧振子振动,单摆做小角度摆动 敲锣打鼓发出的声音越来越弱
[试题案例]
[例1] (多选)一单摆做阻尼振动,则在振动过程中( )
A.振幅越来越小,周期也越来越小
B.振幅越来越小,周期不变
C.在振动过程中,通过某一位置时,机械能始终不变
D.在振动过程中,机械能不守恒,周期不变
解析 因单摆做阻尼振动,所以振幅越来越小,机械能越来越小,振动周期不变。
答案 BD
规律总结 阻尼振动的能量和周期
(1)阻尼振动的振幅不断减小,能量不断减少,但阻尼振动的频率不变,其频率为固有频率,由系统本身决定。
(2)自由振动是一种理想情况,也叫简谐运动。实际中的振动都会受到阻力的作用,当阻力较小时,可认为是简谐运动。
(3)阻尼振动中,机械能E等于动能Ek和势能Ep之和,即E=Ek+Ep,E减小,但动能和势能相互转化,当Ep相等时,Ek不相等。
[针对训练1] (多选)如图所示是单摆做阻尼振动的振动图线,下列说法中正确的是( )
A.摆球A时刻的动能等于B时刻的动能
B.摆球A时刻的势能等于B时刻的势能
C.摆球A时刻的机械能等于B时刻的机械能
D.摆球A时刻的机械能大于B时刻的机械能
解析 在单摆振动过程中,因不断克服空气阻力做功使振动的能量逐渐转化为内能,C错误,D正确;虽然单摆总的机械能在逐渐减小,但在振动过程中动能和势能仍不断地相互转化。由于A、B两时刻单摆的位移相等,所以势能相等,但动能不相等,A错误,B正确。
答案 BD
核心要点 对受迫振动与共振的理解
[问题探究]
双桶洗衣机在衣服脱水完毕拔掉电源后,电动机还要转动一会才能停下来。在拔掉电源后,发现洗衣机先振动得比较弱,有一阵子振动得很剧烈,然后振动慢慢减弱直至停下来。
(1)开始时,洗衣机为什么振动比较弱?
(2)期间剧烈振动的原因是什么?
答案 (1)开始时,脱水桶转动的频率远高于洗衣机的固有频率,振幅较小,振动比较弱。
(2)当洗衣机脱水桶转动的频率等于洗衣机的固有频率时发生共振,振动剧烈。
[探究归纳]
自由振动、受迫振动、共振的比较
自由振动 受迫振动 共振
振动原因 受回复力 受周期性驱动力作用 受周期性驱动力作用
振动周期或频率 由物体本身性质决定,即固有周期或固有频率 由驱动力的周期或频率决定,即T=T驱或f=f驱 T驱=T固或f驱=f固
振动能量 振动物体的机械能不变 由产生驱动力的物体提供 振动物体获得的能量最大
常见例子 弹簧振子或单摆 扬声器纸盆的振动 路面共振破碎机、音叉共鸣箱
[试题案例]
[例2] 如图所示,在一条张紧的绳上挂7个摆,先让A摆振动起来,则其余各摆也随之振动。已知A、B、F三摆的摆长相同,则下列判断正确的是( )
A.7个摆的固有频率都相同
B.振动稳定后7个摆的振动频率各不相同
C.B、F摆的摆长与A摆相同,它们的振幅最大
D.除A摆外,D、E摆离A摆最近,它们的振幅最大
解析 7个摆的摆长不完全相同,固有频率不完全相同,选项A错误;A摆振动起来后,带动其余6个摆做受迫振动,振动稳定后7个摆的振动频率都相同,选项B错误;B、F摆的摆长与A摆相同,发生共振,选项C正确,D错误。
答案 C
[针对训练2] 一个单摆做受迫振动,其共振曲线(振幅A与驱动力的频率f的关系)如图所示,则( )
A.此单摆的固有周期约为0.5 s
B.此单摆的摆长约为1 m
C.若摆长增大,单摆的固有频率增大
D.若摆长增大,共振曲线的峰将向右移动
解析 由共振条件知单摆的固有频率为f=0.5 Hz,则其固有周期为T==2 s,选项A错误;由单摆周期公式T=2π,可求得单摆摆长为l=≈1 m,选项B正确;摆长增大,单摆的固有周期变大,其固有频率变小,共振曲线的峰将向左移动,选项C、D错误。
答案 B
1.(对阻尼振动的理解)(多选)一单摆在空气中振动,振幅逐渐减小,下列说法正确的是( )
A.振动的机械能逐渐转化为其他形式的能
B.后一时刻的动能一定小于前一时刻的动能
C.后一时刻的势能一定小于前一时刻的势能
D.后一时刻的机械能一定小于前一时刻的机械能
解析 单摆振动过程中,会不断克服空气阻力做功使机械能逐渐减小,A、D正确;虽然单摆总的机械能在逐渐减小,但在振动过程中动能和势能仍不断地相互转化。动能转化为势能时,动能逐渐减少,势能逐渐增加,而势能转化为动能时,势能逐渐减少,动能逐渐增加,所以不能断言后一时刻的动能(或势能)一定小于前一时刻的动能(或势能),故B、C错误。
答案 AD
2.(对受迫振动的理解)如图所示的装置,弹簧振子的固有频率是4 Hz。现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为1 Hz,则把手转动的频率为( )
A.1 Hz B.3 Hz
C.4 Hz D.5 Hz
解析 因把手每转动一周,驱动力完成一次周期性变化,即把手转动频率即为驱动力的频率。弹簧振子做受迫振动,而受迫振动的频率等于驱动力的频率,与振动系统的固有频率无关,故A正确。
答案 A
3.(受迫振动、共振)(多选)如图所示,在一根张紧的水平绳上悬挂五个摆,其中A、E的摆长为l,B的摆长为0.5l,C的摆长为1.5l,D的摆长为2l,先使A振动起来,其他各摆随后也振动起来,则摆球振动稳定后( )
A.D的振幅一定最大 B.E的振幅一定最大
C.B的周期一定最短 D.其余四个摆的周期相同
解析 A振动起来后,使得B、C、D、E做受迫振动,振动的频率都等于A振动的频率,即各摆振动的周期都相等,选项C错误,D正确;由于D与A的摆长相差最大,E与A的摆长相等,所以D的振幅最小,E发生共振,振幅最大,选项A错误,B正确。
答案 BD
4.(共振的防止和利用)(多选)下列关于共振和防止共振的说法,正确的是( )
A.共振现象总是有害的,所以要避免共振现象发生
B.队伍过桥要慢行是为了不产生周期性的驱动力,从而避免产生共振
C.火车过桥慢行是为了使驱动力的频率远小于桥的固有频率,从而避免产生共振
D.利用共振时,应使驱动力的频率接近或等于振动物体的固有频率;防止共振危害时,应使驱动力的频率远离振动物体的固有频率
解析 共振现象不一定总是有害的,有的时候我们要利用共振现象,如共振筛,共振转速计等,故A错误;队伍过桥慢行也会产生周期性的驱动力,即会产生共振,故B错误;火车过桥要慢行,目的是使驱动力频率远小于桥梁的固有频率,以免发生共振损坏桥,C正确;受迫振动的频率等于驱动力的频率,所以利用共振时,应使驱动力的频率接近或等于振动物体的固有频率,防止共振危害时,应尽量使驱动力频率远离振动物体的固有频率,故D正确。
答案 CD
基础过关
1.自由摆动的秋千,摆动的振幅越来越小,下列说法正确的是( )
A.机械能守恒
B.能量正在消失
C.总能量守恒,机械能减小
D.只有动能和势能的相互转化
解析 秋千摆动时受到空气的阻力,秋千的机械能向其他形式的能转化,但总的能量守恒。
答案 C
2.(多选)对于阻尼振动,下列说法正确的是( )
A.阻尼振动就是减幅振动,其振动的能量不断减少
B.实际的振动系统不可避免地要受到阻尼作用
C.阻尼振动的振幅、振动能量、振动周期逐渐减小
D.对做阻尼振动的振子来说,其机械能逐渐转化为内能
解析 振动系统的振动频率与本身的结构有关,为固有频率,所以在阻尼振动中,振幅减小,振动能量减少,最终转化为内能,但周期不变,故A、D正确,C错误;实际的振动系统都要受到摩擦或空气阻力等阻尼作用,故B正确。
答案 ABD
3.下列振动中属于受迫振动的是( )
A.用重锤敲击一下悬吊着的钟后,钟的摆动
B.打点计时器接通电源后,振针的振动
C.小孩睡在自由摆动的吊床上,小孩随着吊床一起摆动
D.弹簧振子在竖直方向上上下振动
解析 受迫振动是振动物体在驱动力作用下的运动,故只有B正确。
答案 B
4.在飞机的发展史中有一个阶段,飞机上天后不久,飞机的机翼(翅膀)很快就抖动起来,而且越抖越厉害。后来经过人们的探索,利用在飞机机翼前缘处装置一个配重杆的方法,解决了这一问题。在飞机机翼前装置配重杆的目的主要是( )
A.加大飞机的惯性 B.使机体更加平衡
C.使机翼更加牢固 D.改变机翼的固有频率
解析 飞机的机翼(翅膀)很快就抖动起来,是因为驱动力的频率接近机翼的固有频率发生共振,在飞机机翼前装置配重杆,是为了改变机翼的固有频率,使驱动力的频率远离机翼的固有频率。故A、B、C错误,D正确。
答案 D
5.部队经过桥梁时,规定不许齐步走,登山运动员登高山时,不许高声叫喊,主要原因是( )
A.减轻对桥的压力,避免产生回声
B.减少对桥、雪山的冲量
C.避免使桥、雪山发生共振
D.使桥受到的压力更不均匀,使登山运动员耗散能量减少
解析 部队过桥时若齐步走会给桥梁施加周期性外力,容易使桥的振动幅度增加,即发生共振,造成桥梁倒塌;登山运动员登高山时高声叫喊,声波容易引发雪山共振而发生雪崩,故选项C正确。
答案 C
6.如图所示是单摆做阻尼振动的位移—时间图线,下列说法中正确的是( )
A.摆球在P与N时刻的势能相等
B.摆球在P与N时刻的动能相等
C.摆球在P与N时刻的机械能相等
D.摆球在P时刻的机械能小于在N时刻的机械能
解析 由于摆球的势能大小由其位移和摆球质量共同决定,P、N两时刻位移大小相同,所以势能相等,A正确;由于系统机械能在减少,P、N两时刻势能相同,则P时刻动能大于N时刻动能,B、C、D错误。
答案 A
7.任何物体都有自己的固有频率。研究表明,如果把人作为一个整体来看,在水平方向上振动时的固有频率约为5 Hz。当工人操作风镐、风铲、铆钉机等振动机械时,操作者在水平方向将做受迫振动。在这种情况下,下列说法正确的是( )
A.操作者的实际振动频率等于他自身的固有频率
B.操作者的实际振动频率等于机械的振动频率
C.为了保证操作者的安全,振动机械的频率应尽量接近人的固有频率
D.为了保证操作者的安全,应尽量提高操作者的固有频率
解析 物体在周期性驱动力作用下做受迫振动,受迫振动的频率等于驱动力的频率,与固有频率无关,可知操作者的实际频率等于机械的振动频率,故A错误,B正确;当驱动力频率等于物体的固有频率时,物体的振幅最大,产生共振现象,所以为了保证操作者的安全,振动机械的频率应尽量远离人的固有频率,操作者的固有频率无法提高,故C、D错误。
答案 B
8.如图所示,三个单摆的摆长分别为l1=1.5 m,l2=1 m,l3=0.5 m,现用一周期等于2 s的驱动力,使它们做受迫振动,那么当它们的振动稳定时,下列判断中正确的是( )
A.三个摆的周期和振幅相等
B.三个摆的周期不等,振幅相等
C.三个摆的周期相等,但振幅不等
D.三个摆的周期和振幅都不相等
解析 三个摆的振动都是受迫振动,所以振动的频率都与驱动力的频率相同,三者的频率相同。由f==知,2的固有频率与驱动力的频率最接近,振幅最大,而1和3的振幅较小,故C正确。
答案 C
9.在实验室可以做“声波碎杯”的实验。用手指轻弹一只酒杯,可以听到清脆的声音,测得该声音的频率为500 Hz。将这只酒杯放在两个大功率的声波发生器之间,操作人员通过调整其发出的声波,就能使酒杯碎掉(如图所示)。下列说法正确的是( )
A.操作人员一定是把声波发生器的功率调到很大
B.操作人员可能是使声波发生器发出了频率很高的超声波
C.操作人员一定是同时增大了声波发生器发出声波的频率和功率
D.操作人员只需将声波发生器发出的声波频率调到500 Hz
解析 驱动力的频率与系统的固有频率相等时,受迫振动的振幅最大,形成共振。操作人员只需将声波发生器发出的声波频率调到500 Hz,就能使酒杯碎掉,D正确。
答案 D
能力提升
10.(多选)铺设铁轨时,每两根钢轨接缝处都必须留有一定的间隙,匀速运行的列车经过轨端接缝处时,车轮就会受到一次冲击。由于每一根钢轨长度相等。所以这个冲击力是周期性的,列车受到周期性的冲击做受迫振动。普通钢轨长为
12.6 m,列车固有振动周期为0.315 s。下列说法正确的是( )
A.列车的危险速率为40 m/s
B.列车过桥需要减速,是为了防止发生共振现象
C.列车运行的振动频率和列车的固有频率总是相等的
D.增加钢轨的长度有利于列车高速运行
解析 对于受迫振动,当驱动力的频率与固有频率相等时将发生共振现象,所以列车的危险速率v==40 m/s,A正确;为了防止共振现象发生,列车过桥需要减速,B正确;列车运行的振动频率等于做受迫振动的驱动力的频率,与列车的固有频率无关,C项错;由v=知L增大时,T不变,v变大,D正确。
答案 ABD
11.(多选)蜘蛛虽有8只眼睛,但视力很差,完全靠感觉来捕食和生活,它的腿能敏捷地感觉到落在丝网上的昆虫对丝网造成的振动。当丝网的振动频率为f=
200 Hz左右时,丝网振动的振幅最大,最大振幅为0.5 cm。已知该丝网共振时,蜘蛛能立即捕捉到丝网上的昆虫。则对于落在丝网上的昆虫( )
A.当其翅膀振动的频率为200 Hz左右时,蜘蛛能立即捕捉到它
B.当其翅膀振动的周期为0.05 s左右时,蜘蛛能立即捕捉到它
C.当其翅膀振动的频率为300 Hz左右时,蜘蛛能立即捕捉到它
D.当其翅膀振动的频率为250 Hz时,该丝网的振幅一定小于0.5 cm
解析 当昆虫翅膀振动的频率与丝网的振动频率相等时,即翅膀振动的频率f′=f=200 Hz时,发生共振,蜘蛛能立即捕捉到昆虫,故A正确,C错误;根据周期与频率之间的关系得:T== s=0.005 s,即当昆虫翅膀振动的周期为0.005 s左右时,蜘蛛能立即捕捉到它,故B错误;当昆虫翅膀振动的频率为250 Hz左右时,没有发生共振,故该丝网的振幅小于0.5 cm,故D正确。
答案 AD
12.(多选)如图所示为两个单摆做受迫振动的共振曲线,则下列说法正确的是( )
A.两个单摆的固有周期之比为TⅠ∶TⅡ=5∶2
B.若两个受迫振动在地球上同一地点进行,则两个摆长之比为lⅠ∶lⅡ=4∶25
C.图线Ⅱ若是在地面上完成的,则该摆摆长约为1 m
D.若两个受迫振动分别在月球上和地球上进行,且摆长相等,则图线Ⅱ是月球上的单摆的共振曲线
解析 由共振曲线及共振的条件可知,Ⅰ和Ⅱ的固有频率分别为0.2 Hz和0.5 Hz,周期之比TⅠ∶TⅡ=5∶2,A正确;由单摆的周期公式T=2π可知,lⅠ∶lⅡ=T∶T=25∶4,B错误;同时可知lⅡ≈g,4π2)≈1 m,C正确;当摆长相等时,重力加速度越大,频率越大,月球表面重力加速度小于地球表面重力加速度,故D错误。
答案 AC
13.(多选)把一个筛子用四根弹簧支起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛(如图所示)。不开电动机让这个筛子自由振动时,完成20次全振动用15 s;在某电压下,电动偏心轮的转速是88 r/min。已知增大电动偏心轮的电压可以使其转速提高,而增加筛子的总质量可以增大筛子的固有周期。为使共振筛的振幅增大,以下做法可行的是( )
A.降低输入电压 B.提高输入电压
C.增加筛子质量 D.减小筛子质量
解析 筛子的固有频率为f固= Hz= Hz,而当时的驱动力频率为f驱= Hz= Hz,即f固
14.如图所示,曲轴上悬挂一弹簧振子,转动摇把,曲轴可以带动弹簧振子上下振动。
(1)开始时不转动摇把,而用手往下拉振子,然后放手让振子上下振动,测得振子在10 s内完成20次振动,不考虑摩擦力和空气阻力,振子做什么振动?其固有周期和固有频率各是多少?若考虑摩擦力和空气阻力,振子做什么振动?
(2)在振子正常振动过程中,以转速4 r/s匀速转动把手,振子的振动稳定后,振子做什么运动?其周期是多少?
解析 (1)用手往下拉振子,放手后,因振子所受回复力满足F=-kx,所以做简谐运动,根据题意T固== s=0.5 s。f固== Hz=2 Hz,由于摩擦力和空气阻力的存在,振子克服摩擦力和阻力做功消耗能量,使其振幅越来越小,故振动为阻尼振动。
(2)由于把手转动的转速为4 r/s,它给弹簧振子的驱动力频率为f驱=4 Hz,周期T驱=0.25 s,故振子做受迫振动.振动达稳定状态后,其频率(或周期)等于驱动力的频率(或周期),而跟固有频率(或周期)无关。即f=f驱=4 Hz,T=T驱=0.25 s。
答案 (1)简谐运动 0.5 s 2 Hz 阻尼振动
(2)受迫振动 0.25 s
15.火车在轨道上行驶时,由于在钢轨接头处车轮受到撞击而上下振动。如果防震弹簧每受104 N的力将被压缩20 mm,而每根弹簧的实际负荷为5 000 kg,已知弹簧的振动周期T=2π,设钢轨长为12.5 m,问车速为多大时,火车振动得最剧烈?
解析 由题意可知弹簧在做受迫振动,弹簧发生共振时,振动最强烈,此时必须满足:f驱=f固(或T驱=T固)。
根据题意知,防震弹簧的劲度系数为
k== N/m=5×105 N/m
由于每根弹簧的实际负荷为m=5 000 kg,
所以弹簧的固有周期为
T固=2π=2π s= s
当振动最强烈时有T驱=== s
故火车的速度为v≈19.9 m/s。
答案 19.9 m/s
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
