粤教版(2019)高中物理 必修第一册 第3章 章末综合提升学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第一册 第3章 章末综合提升学案 | 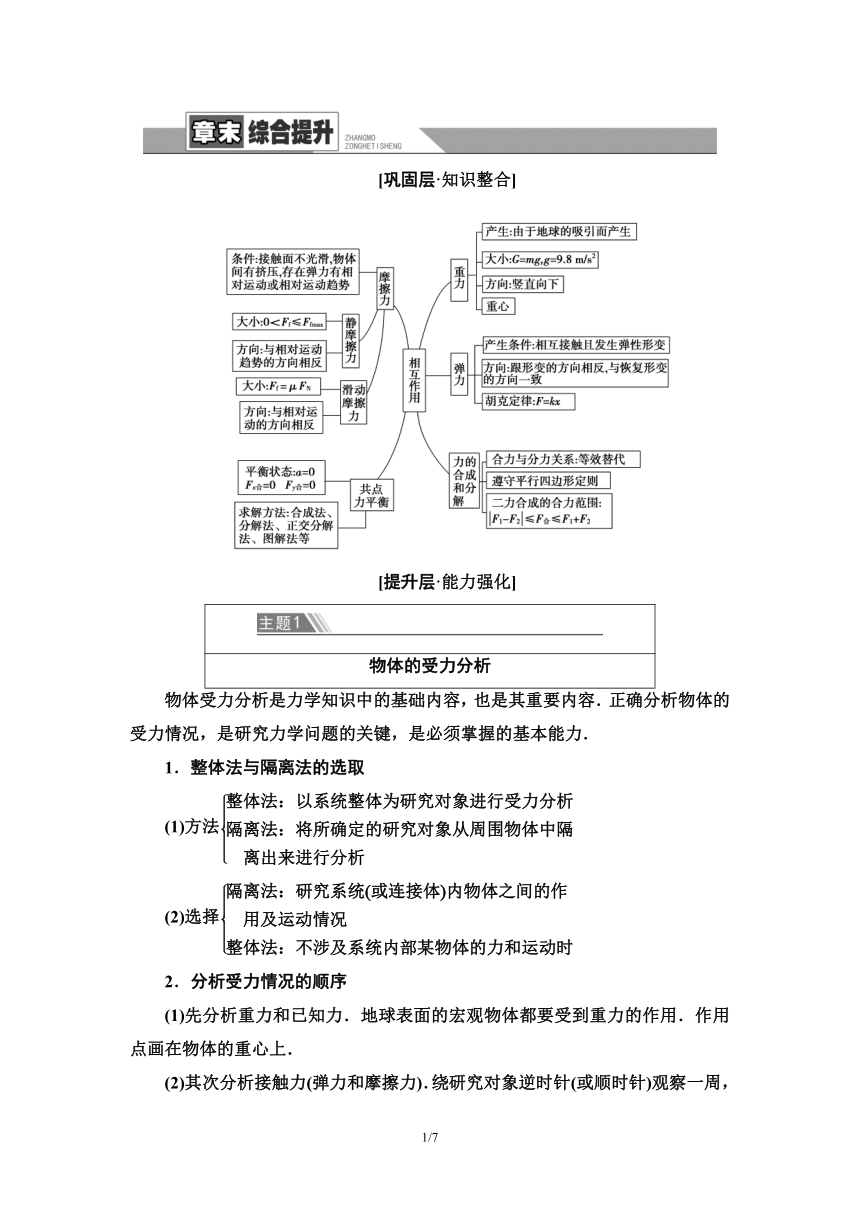 | |
| 格式 | doc | ||
| 文件大小 | 425.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-05 22:26:53 | ||
图片预览



文档简介
[巩固层·知识整合]
[提升层·能力强化]
物体的受力分析
物体受力分析是力学知识中的基础内容,也是其重要内容.正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本能力.
1.整体法与隔离法的选取
(1)方法
(2)选择
2.分析受力情况的顺序
(1)先分析重力和已知力.地球表面的宏观物体都要受到重力的作用.作用点画在物体的重心上.
(2)其次分析接触力(弹力和摩擦力).绕研究对象逆时针(或顺时针)观察一周,看研究对象跟其他物体有几个(N个)接触点(或面),则最多有几个(N个)弹力.某个接触点(或面)有挤压,则画出弹力;若还有相对运动(或相对运动趋势),则画出摩擦力.
(3)画完受力图后再进行检查,看是否多画了力或漏力的现象,物体的受力情况和运动状态是否相符,然后加以纠正.
3.受力分析注意问题
(1)分析物体受力时,只分析周围物体对研究对象所施加的力,不要分析研究对象对周围物体施加的力,也不要把作用在其他物体上的力错误地认为通过“力的传递”作用在研究对象上.
(2)受力分析时,不要多画不存在的力或漏力,要注意确定每个力的施力物体和受力物体,在力的合成和分解中,不要把实际不存在的合力或分力当作是物体受到的力.
(3)如果一个力的方向难以确定,可用假设法分析.
(4)物体受力情况会随运动状态的改变而改变,必要时要根据学到的知识通过计算确定.
(5)受力分析须严密,外部作用看整体,互相作用要隔离.找施力物体防“添力”,顺序分析防“漏力”;分力和合力避免重复,性质力、效果力避免重记.
【例1】 如图所示,用轻质细线把两个质量未知的小球悬挂起来.今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是( )
A [表示平衡状态的图是哪一个,关键是要求出两条轻质细绳对小球a和小球b的拉力的方向,只要拉力方向找出后,图就确定了.
先以小球a、b及连线组成的整体为研究对象,系统共受五个力的作用,即两个重力(ma+mb)g,作用在两个小球上的恒力Fa、Fb和上端细线对系统的拉力T1.因为系统处于平衡状态,所受合力必为零,由于Fa、Fb大小相等,方向相反,可以抵消,而(ma+mb)g的方向竖直向下,所以悬线对系统的拉力T1的方向必然竖直向上.再以b球为研究对象,b球在重力mbg、恒力Fb和连线拉力T2′三个力的作用下处于平衡状态,已知恒力向右偏上30°,重力竖直向下,所以平衡时连线拉力T2′的方向必与恒力Fb和重力mbg的合力方向相反,如图所示,故应选A.]
受力分析的常用方法
1.整体法与隔离法.
2.假设法.
3.利用作用力与反作用力.
4.共点力平衡法.
动态平衡问题
1.所谓动态平衡问题是指通过控制某些物理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态.
2.解决动态平衡问题常用的方法有三种
(1)解析法:对研究对象的任一状态进行受力分析,利用三角形的知识建立平衡方程,求出因变量与自变量的一般函数式,然后依据自变量的变化确定因变量的变化(自变量一般为某个力与水平方向或竖直方向的夹角).
(2)图解法:利用图解法解决此类问题的基本方法是:对研究对象在状态变化过程中的若干状态进行受力分析,依据某一参量的变化,在同一图中作出物体在若干状态下的平衡力图(力的平行四边形),再由动态的力四边形各边长度变化及角度变化确定力的大小及方向的变化情况.如图所示,将重球用绳挂在光滑墙上,当保持球的重力不变而增大球的半径时,就属于一个动态平衡问题.首先分析球的受力情况,F1与F2的合力F大小等于G,在球半径增大时F的大小和方向不变,F2的方向不变,α增大,画出几个位置的情况.A、A′、A″及B、B′、B″,由图可知F1增大,F2也增大.
(3)相似三角形法:在运算过程中既找不到直角三角形也不符合图解法的条件,但是力的三角形与几何三角形相似,则可利用三角形相似,对应边成比例,依据几何三角形的边长变化判断力的大小变化情况.
【例2】 (多选)如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角为α(α>).现将重物向右上方缓慢拉起,并保持夹角α不变.在OM由竖直被拉到水平的过程中( )
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
AD [以重物为研究对象,它受三个力即重力mg、绳OM段的拉力FO、NM段的拉力FN的作用处于平衡状态.考虑到重力mg不变,FO与FN的夹角不变,当FO由竖直向上变为水平向左时,作出如图所示力的矢量图,由图可知:FN一直变大,FO先变大后减小.
]
(1)图解法常用于分析三个力中有一个力不变,另一个力的方向不变的动态平衡问题.
(2)本题中,三个力中有两个力的方向在变化,利用图解法分析时应抓住问题的特点,如本题中变化的两个力间的夹角是一定的,且另一个力mg是不变的,考虑这些特点,就会联想到辅助圆.
摩擦力“突变”问题的分析
在外界因素变化的过程中,摩擦力的性质会发生变化,如由静摩擦力变为滑动摩擦力,或由滑动摩擦力变为静摩擦力.摩擦力的突变情况如下表:
分类 说明 案例图示
静—静“突变” 物体在摩擦力和其他力作用下处于平衡状态,当作用在物体上的其他力发生突变时,如果物体仍能保持平衡状态,则物体受到的摩擦力的大小或方向将会发生“突变” 在水平力F作用下物体静止于斜面,F突然增大时物体仍静止,则所受静摩擦力大小或方向将“突变”
静—动“突变” 物体在摩擦力和其他力作用下处于静止状态,当其他力变化时,如果物体不能保持静止状态,则物体受到的静摩擦力将“突变”为滑动摩擦力 放在粗糙水平面上的物体,水平力F从零逐渐增大,物体开始滑动时,物体受到地面的摩擦力由静摩擦力“突变”为滑动摩擦力
动—静“突变” 在摩擦力和其他力作用下,做减速运动的物体突然停止滑行时,物体将不受摩擦力作用,或滑动摩擦力“突变”为静摩擦力 滑块以v0冲上斜面做减速运动,当到达某位置静止时,滑动摩擦力“突变”为静摩擦力
【例3】 (多选)一个物块位于斜面上,受到平行于斜面的水平力F的作用处于静止状态,如图所示,如果将外力F撤去,则物块( )
A.会沿斜面下滑
B.摩擦力方向一定变化
C.摩擦力的值变大
D.摩擦力的值变小
BD [物块静止于斜面上时,在斜面所在平面上的受力情况如图所示,它受三个力作用:水平力F、静摩擦力f和物块的重力沿斜面向下的分力Gsin θ.物块处于平衡状态,三个力的合力为零.由图可知,静摩擦力f大于Gsin θ.而最大静摩擦力不会小于静摩擦力,所以斜面对物块的最大静摩擦力大于Gsin θ.如果将外力F撤去,因为斜面对物块的最大静摩擦力大于Gsin θ,则物块仍然静止于斜面上,这时在斜面所在平面上,它受两个力的作用:物块的重力沿斜面向下的分力Gsin θ和斜面对物块的沿斜面向上的静摩擦力(大小为Gsin θ).其中,在撤去外力F的时刻,静摩擦力发生了突变:方向由原来沿斜面的右上方突变为沿斜面向上,大小由大于Gsin θ变为等于Gsin θ.]
物体受到的外力发生变化时,物体受到的摩擦力就有可能发生突变.解决这类问题的关键是:正确对物体进行受力分析和运动状态分析,从而找到物体摩擦力的突变“临界点”.
[培养层·素养升华]
有些电梯修理员、牵引专家等,常需要知道绳(或金属线)中的张力FT,可又不便到绳(或线)的自由端去测量。现某家公司制造了一种夹在绳上的仪表(如图中B、C为该夹子的横截面).测量时,只要如图示那样用一硬杆竖直向上作用在绳上的某点A,使绳产生一个微小偏移量a,借助仪表很容易测出这时绳对硬杆的压力F.现测得该微小偏移量a=12 mm,B、C间的距离2L=250 mm,绳对杆的压力F=300 N.
[设问探究]
(1)试求绳中的张力FT(结果保留两位有效数字);
(2)请说明为什么能用很小的力就能测较大的力.
提示:(1)A点受力如答图所示,由平衡条件根据力的合成得F=2FTsin α,当α很小时,sin α=tan α.由几何关系得tan α=,解得FT=,代入数据得FT=1.6×103 N.
(2)由(1)问中知FT=,因为的比值很大,所以的比值也很大,所以很省力.
7/7
[提升层·能力强化]
物体的受力分析
物体受力分析是力学知识中的基础内容,也是其重要内容.正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本能力.
1.整体法与隔离法的选取
(1)方法
(2)选择
2.分析受力情况的顺序
(1)先分析重力和已知力.地球表面的宏观物体都要受到重力的作用.作用点画在物体的重心上.
(2)其次分析接触力(弹力和摩擦力).绕研究对象逆时针(或顺时针)观察一周,看研究对象跟其他物体有几个(N个)接触点(或面),则最多有几个(N个)弹力.某个接触点(或面)有挤压,则画出弹力;若还有相对运动(或相对运动趋势),则画出摩擦力.
(3)画完受力图后再进行检查,看是否多画了力或漏力的现象,物体的受力情况和运动状态是否相符,然后加以纠正.
3.受力分析注意问题
(1)分析物体受力时,只分析周围物体对研究对象所施加的力,不要分析研究对象对周围物体施加的力,也不要把作用在其他物体上的力错误地认为通过“力的传递”作用在研究对象上.
(2)受力分析时,不要多画不存在的力或漏力,要注意确定每个力的施力物体和受力物体,在力的合成和分解中,不要把实际不存在的合力或分力当作是物体受到的力.
(3)如果一个力的方向难以确定,可用假设法分析.
(4)物体受力情况会随运动状态的改变而改变,必要时要根据学到的知识通过计算确定.
(5)受力分析须严密,外部作用看整体,互相作用要隔离.找施力物体防“添力”,顺序分析防“漏力”;分力和合力避免重复,性质力、效果力避免重记.
【例1】 如图所示,用轻质细线把两个质量未知的小球悬挂起来.今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是( )
A [表示平衡状态的图是哪一个,关键是要求出两条轻质细绳对小球a和小球b的拉力的方向,只要拉力方向找出后,图就确定了.
先以小球a、b及连线组成的整体为研究对象,系统共受五个力的作用,即两个重力(ma+mb)g,作用在两个小球上的恒力Fa、Fb和上端细线对系统的拉力T1.因为系统处于平衡状态,所受合力必为零,由于Fa、Fb大小相等,方向相反,可以抵消,而(ma+mb)g的方向竖直向下,所以悬线对系统的拉力T1的方向必然竖直向上.再以b球为研究对象,b球在重力mbg、恒力Fb和连线拉力T2′三个力的作用下处于平衡状态,已知恒力向右偏上30°,重力竖直向下,所以平衡时连线拉力T2′的方向必与恒力Fb和重力mbg的合力方向相反,如图所示,故应选A.]
受力分析的常用方法
1.整体法与隔离法.
2.假设法.
3.利用作用力与反作用力.
4.共点力平衡法.
动态平衡问题
1.所谓动态平衡问题是指通过控制某些物理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态.
2.解决动态平衡问题常用的方法有三种
(1)解析法:对研究对象的任一状态进行受力分析,利用三角形的知识建立平衡方程,求出因变量与自变量的一般函数式,然后依据自变量的变化确定因变量的变化(自变量一般为某个力与水平方向或竖直方向的夹角).
(2)图解法:利用图解法解决此类问题的基本方法是:对研究对象在状态变化过程中的若干状态进行受力分析,依据某一参量的变化,在同一图中作出物体在若干状态下的平衡力图(力的平行四边形),再由动态的力四边形各边长度变化及角度变化确定力的大小及方向的变化情况.如图所示,将重球用绳挂在光滑墙上,当保持球的重力不变而增大球的半径时,就属于一个动态平衡问题.首先分析球的受力情况,F1与F2的合力F大小等于G,在球半径增大时F的大小和方向不变,F2的方向不变,α增大,画出几个位置的情况.A、A′、A″及B、B′、B″,由图可知F1增大,F2也增大.
(3)相似三角形法:在运算过程中既找不到直角三角形也不符合图解法的条件,但是力的三角形与几何三角形相似,则可利用三角形相似,对应边成比例,依据几何三角形的边长变化判断力的大小变化情况.
【例2】 (多选)如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角为α(α>).现将重物向右上方缓慢拉起,并保持夹角α不变.在OM由竖直被拉到水平的过程中( )
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
AD [以重物为研究对象,它受三个力即重力mg、绳OM段的拉力FO、NM段的拉力FN的作用处于平衡状态.考虑到重力mg不变,FO与FN的夹角不变,当FO由竖直向上变为水平向左时,作出如图所示力的矢量图,由图可知:FN一直变大,FO先变大后减小.
]
(1)图解法常用于分析三个力中有一个力不变,另一个力的方向不变的动态平衡问题.
(2)本题中,三个力中有两个力的方向在变化,利用图解法分析时应抓住问题的特点,如本题中变化的两个力间的夹角是一定的,且另一个力mg是不变的,考虑这些特点,就会联想到辅助圆.
摩擦力“突变”问题的分析
在外界因素变化的过程中,摩擦力的性质会发生变化,如由静摩擦力变为滑动摩擦力,或由滑动摩擦力变为静摩擦力.摩擦力的突变情况如下表:
分类 说明 案例图示
静—静“突变” 物体在摩擦力和其他力作用下处于平衡状态,当作用在物体上的其他力发生突变时,如果物体仍能保持平衡状态,则物体受到的摩擦力的大小或方向将会发生“突变” 在水平力F作用下物体静止于斜面,F突然增大时物体仍静止,则所受静摩擦力大小或方向将“突变”
静—动“突变” 物体在摩擦力和其他力作用下处于静止状态,当其他力变化时,如果物体不能保持静止状态,则物体受到的静摩擦力将“突变”为滑动摩擦力 放在粗糙水平面上的物体,水平力F从零逐渐增大,物体开始滑动时,物体受到地面的摩擦力由静摩擦力“突变”为滑动摩擦力
动—静“突变” 在摩擦力和其他力作用下,做减速运动的物体突然停止滑行时,物体将不受摩擦力作用,或滑动摩擦力“突变”为静摩擦力 滑块以v0冲上斜面做减速运动,当到达某位置静止时,滑动摩擦力“突变”为静摩擦力
【例3】 (多选)一个物块位于斜面上,受到平行于斜面的水平力F的作用处于静止状态,如图所示,如果将外力F撤去,则物块( )
A.会沿斜面下滑
B.摩擦力方向一定变化
C.摩擦力的值变大
D.摩擦力的值变小
BD [物块静止于斜面上时,在斜面所在平面上的受力情况如图所示,它受三个力作用:水平力F、静摩擦力f和物块的重力沿斜面向下的分力Gsin θ.物块处于平衡状态,三个力的合力为零.由图可知,静摩擦力f大于Gsin θ.而最大静摩擦力不会小于静摩擦力,所以斜面对物块的最大静摩擦力大于Gsin θ.如果将外力F撤去,因为斜面对物块的最大静摩擦力大于Gsin θ,则物块仍然静止于斜面上,这时在斜面所在平面上,它受两个力的作用:物块的重力沿斜面向下的分力Gsin θ和斜面对物块的沿斜面向上的静摩擦力(大小为Gsin θ).其中,在撤去外力F的时刻,静摩擦力发生了突变:方向由原来沿斜面的右上方突变为沿斜面向上,大小由大于Gsin θ变为等于Gsin θ.]
物体受到的外力发生变化时,物体受到的摩擦力就有可能发生突变.解决这类问题的关键是:正确对物体进行受力分析和运动状态分析,从而找到物体摩擦力的突变“临界点”.
[培养层·素养升华]
有些电梯修理员、牵引专家等,常需要知道绳(或金属线)中的张力FT,可又不便到绳(或线)的自由端去测量。现某家公司制造了一种夹在绳上的仪表(如图中B、C为该夹子的横截面).测量时,只要如图示那样用一硬杆竖直向上作用在绳上的某点A,使绳产生一个微小偏移量a,借助仪表很容易测出这时绳对硬杆的压力F.现测得该微小偏移量a=12 mm,B、C间的距离2L=250 mm,绳对杆的压力F=300 N.
[设问探究]
(1)试求绳中的张力FT(结果保留两位有效数字);
(2)请说明为什么能用很小的力就能测较大的力.
提示:(1)A点受力如答图所示,由平衡条件根据力的合成得F=2FTsin α,当α很小时,sin α=tan α.由几何关系得tan α=,解得FT=,代入数据得FT=1.6×103 N.
(2)由(1)问中知FT=,因为的比值很大,所以的比值也很大,所以很省力.
7/7
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
