人教版八年级数学上册 11.3.2 多边形的内角和 课件(第二课时 23张)
文档属性
| 名称 | 人教版八年级数学上册 11.3.2 多边形的内角和 课件(第二课时 23张) |  | |
| 格式 | zip | ||
| 文件大小 | 408.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 13:14:05 | ||
图片预览




文档简介
(共23张PPT)
11.3
多边形的内角和
第2课时
问题:1、三角形的内角和是_______;
正方形的内角和是________;
一般四边形的内角和是多少呢?
2.五边形的内角和呢?
3.n边形的内角和是多少呢?
创设情景
明确目标
B
A
C
D
E
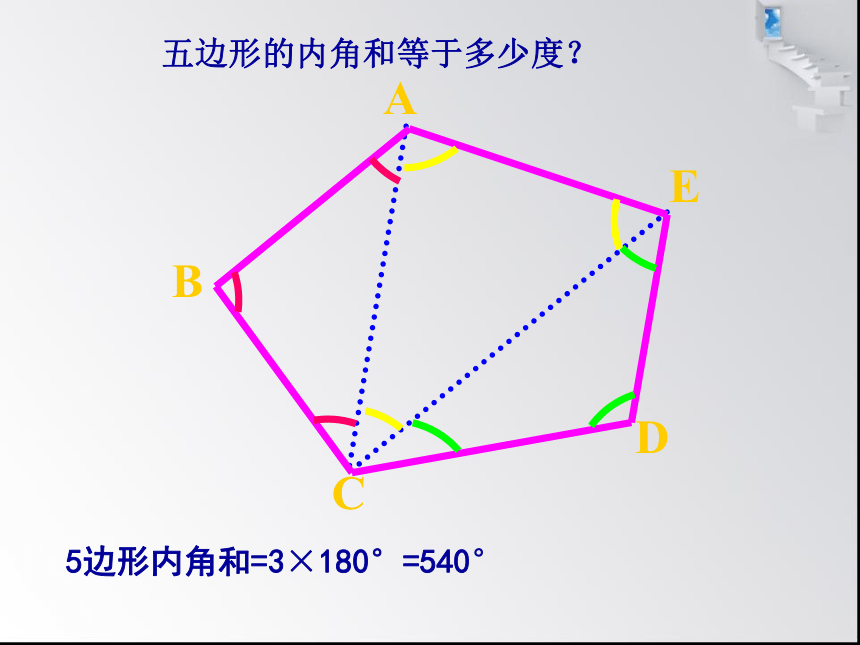
5边形内角和=3×180°=540°
五边形的内角和等于多少度?
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2)
·180°
(7-2)
×180°
(6-2)×180°
(5-2)
×180°
(4-2)
×180°
(3-2)
×180°
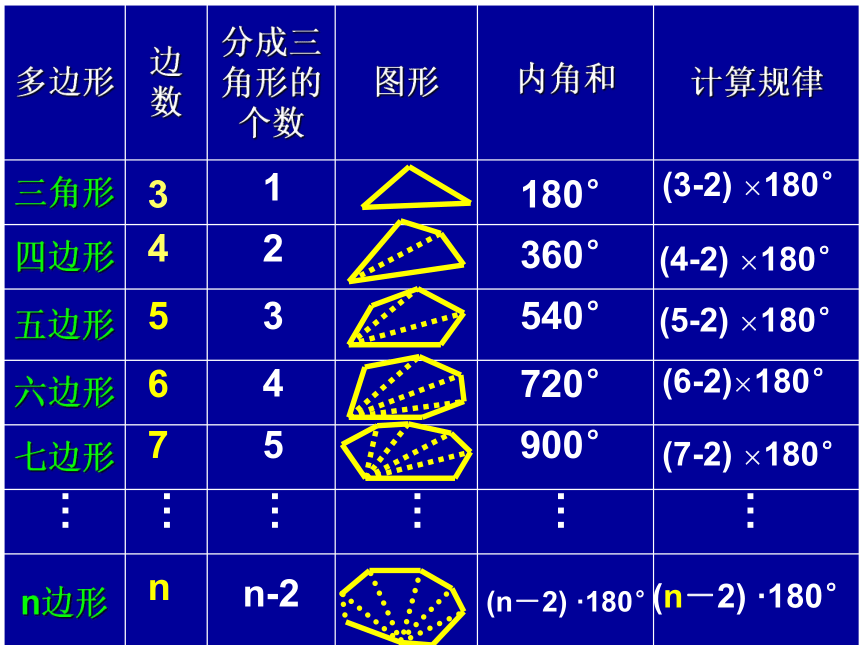
n边形内角和公式
n边形内角和=(n-2)·180°
口答:
三角形、四边形、五边形、六边形的内角和分别是多少度?
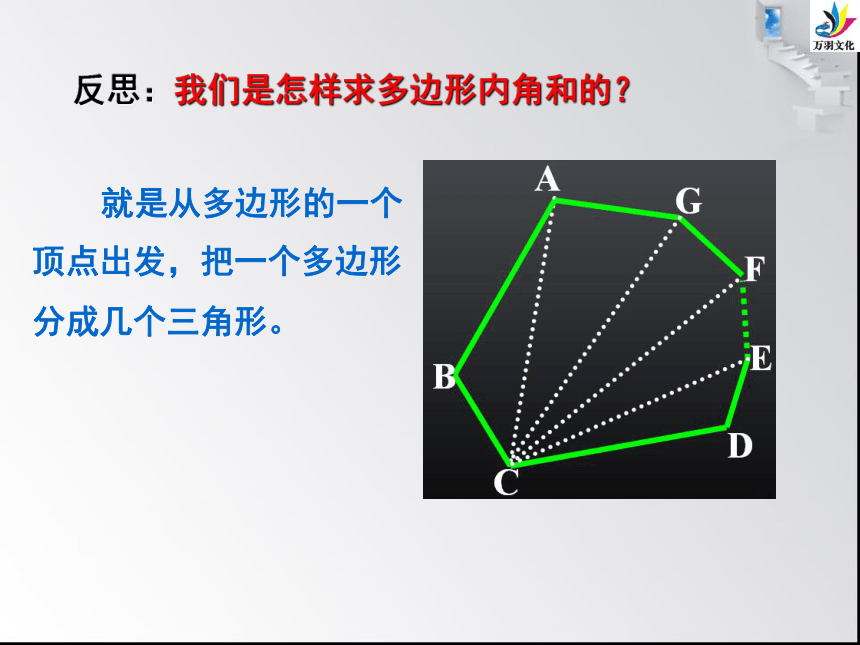
反思:我们是怎样求多边形内角和的?
就是从多边形的一个顶点出发,把一个多边形分成几个三角形。
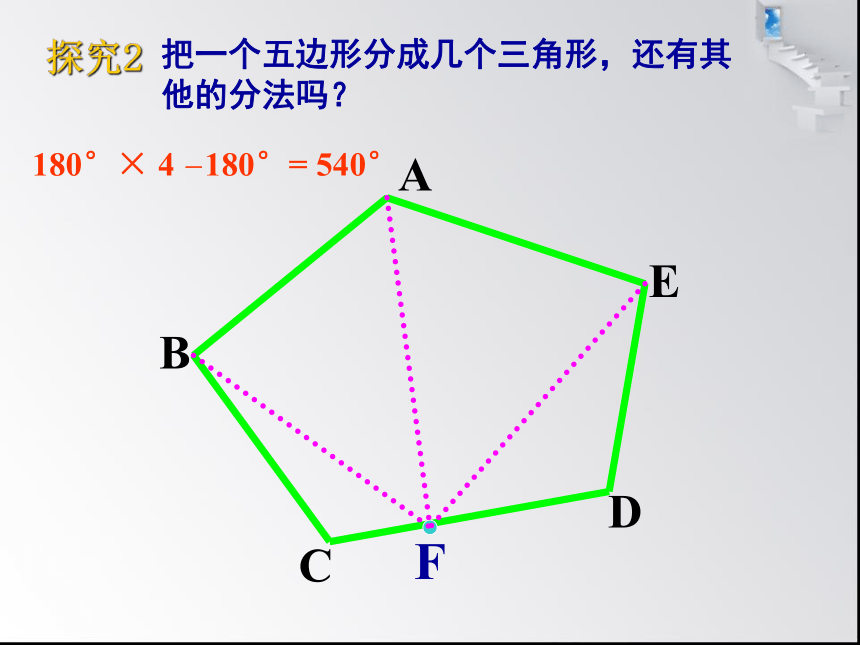
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°×
4
-180°=
540°
探究2
E
A
B
C
D
O
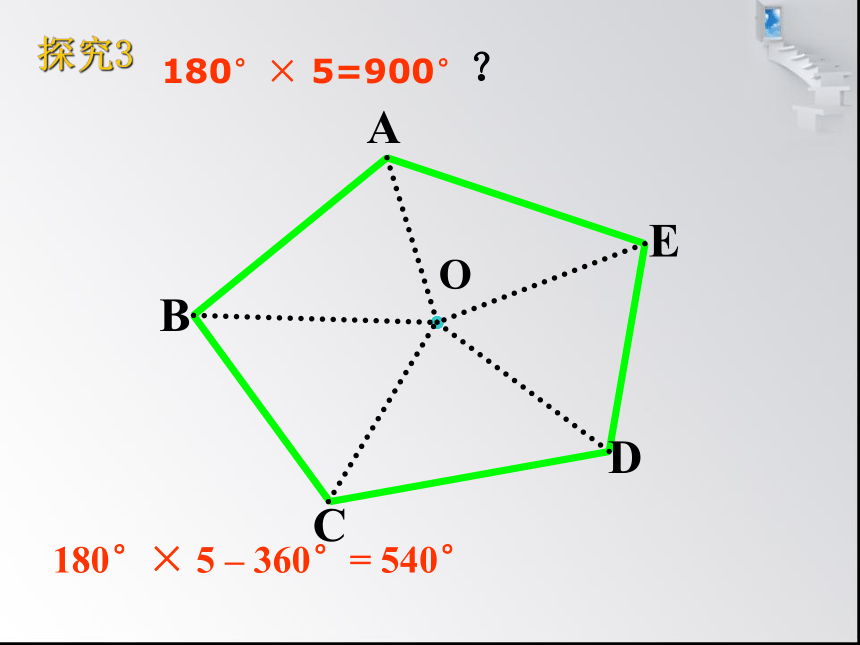
探究3
180°×
5
–
360°=
540°
180°×
5=900°?
十二边形的内角和是(
)。
一个多边形当边数增加1时,它的内角和增加(
),它的外角和增加(
)
一个多边形的内角和是720?,则此多边形共有(
)个内角。
如果一个多边形的内角和是1440度,那么这是(
)边形。
1800?
180?
6
十
0?
5.如图:
求∠A+
∠B+
∠C+
∠D+
∠E+
∠F=?
E
6、如图:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G=?
F
A
B
C
D
E
G
解:如图,四边形ABCD
中,
∠A
+∠C
=180°.
∵ ∠A
+∠B
+∠C
+∠D
=(4
-
2)×180°
=360°,
∴ ∠B
+∠D
=360°-(∠A
+
∠C)
=360°-
180°
=180°.
例题解析
例2 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
例2
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.试问:五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
6
例2
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
五边形的外角和等于360°
-(5-2)
×
180°
=360
°
=5个平角
-5边形内角和
=5×180°
E
B
C
D
1
2
3
4
5
A
6
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
(1)通过这节课的学习你有哪些收获?
(2)我们是怎样得到多边形内角和公式的?
(3)在探究多边形内角和公式中,连接对角线
起到什么作用?
总结梳理
内化目标
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360
°
达标检测
反思目标
2、正五边形的每一个外角等于____,每一个内角等于__________。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
3、已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360?,
∴
(n-2)?180°=2×
360?。
解得:
n=6
∴这个多边形的边数为6
拓广练习:
1、在多边形的所有外角中最多有几个钝角?在多边形的所有内角中最多有几个锐角?
2、小军在进行多边形内角和计算时,求得的内角和为1125
°,当发现错了之后,重新检查,发现是少加了一个内角,求:
(1)这个多边形是几边形?
(2)这个内角是多少度?
上交作业:
教科书第25页
第7,8,9,10题
.
课后作业:同步练习册相应习题.
课后作业
11.3
多边形的内角和
第2课时
问题:1、三角形的内角和是_______;
正方形的内角和是________;
一般四边形的内角和是多少呢?
2.五边形的内角和呢?
3.n边形的内角和是多少呢?
创设情景
明确目标
B
A
C
D
E
5边形内角和=3×180°=540°
五边形的内角和等于多少度?
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2)
·180°
(7-2)
×180°
(6-2)×180°
(5-2)
×180°
(4-2)
×180°
(3-2)
×180°
n边形内角和公式
n边形内角和=(n-2)·180°
口答:
三角形、四边形、五边形、六边形的内角和分别是多少度?
反思:我们是怎样求多边形内角和的?
就是从多边形的一个顶点出发,把一个多边形分成几个三角形。
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°×
4
-180°=
540°
探究2
E
A
B
C
D
O
探究3
180°×
5
–
360°=
540°
180°×
5=900°?
十二边形的内角和是(
)。
一个多边形当边数增加1时,它的内角和增加(
),它的外角和增加(
)
一个多边形的内角和是720?,则此多边形共有(
)个内角。
如果一个多边形的内角和是1440度,那么这是(
)边形。
1800?
180?
6
十
0?
5.如图:
求∠A+
∠B+
∠C+
∠D+
∠E+
∠F=?
E
6、如图:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G=?
F
A
B
C
D
E
G
解:如图,四边形ABCD
中,
∠A
+∠C
=180°.
∵ ∠A
+∠B
+∠C
+∠D
=(4
-
2)×180°
=360°,
∴ ∠B
+∠D
=360°-(∠A
+
∠C)
=360°-
180°
=180°.
例题解析
例2 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
例2
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.试问:五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
6
例2
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
五边形的外角和等于360°
-(5-2)
×
180°
=360
°
=5个平角
-5边形内角和
=5×180°
E
B
C
D
1
2
3
4
5
A
6
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
(1)通过这节课的学习你有哪些收获?
(2)我们是怎样得到多边形内角和公式的?
(3)在探究多边形内角和公式中,连接对角线
起到什么作用?
总结梳理
内化目标
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360
°
达标检测
反思目标
2、正五边形的每一个外角等于____,每一个内角等于__________。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
3、已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360?,
∴
(n-2)?180°=2×
360?。
解得:
n=6
∴这个多边形的边数为6
拓广练习:
1、在多边形的所有外角中最多有几个钝角?在多边形的所有内角中最多有几个锐角?
2、小军在进行多边形内角和计算时,求得的内角和为1125
°,当发现错了之后,重新检查,发现是少加了一个内角,求:
(1)这个多边形是几边形?
(2)这个内角是多少度?
上交作业:
教科书第25页
第7,8,9,10题
.
课后作业:同步练习册相应习题.
课后作业
