北师版数学八年级上册5.7 用二元一次方程组确定一次函数表达式 课件(22张)
文档属性
| 名称 | 北师版数学八年级上册5.7 用二元一次方程组确定一次函数表达式 课件(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 791.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:46:13 | ||
图片预览






文档简介
5.7 用二元一次方程组确定
一次函数表达式
1.二元一次方程组与一次函数有何联系?
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点坐标也是它们所对应的二元一次方程组的解.
2.二元一次方程组有哪些解法?
消元法
图象法
是一种代数方法
导入新知
1. 了解待定系数法,会用二元一次方程组确定一次函数的表达式.
2. 会应用方程与函数的联系解决实际问题.
素养目标
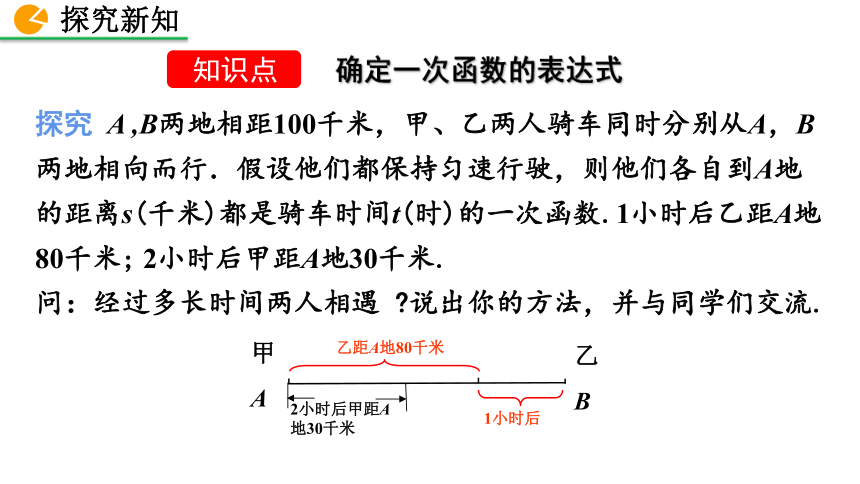
探究 A ,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.1小时后乙距A地80千米; 2小时后甲距A地30千米.
问:经过多长时间两人相遇 ?说出你的方法,并与同学们交流.
1小时后
2小时后甲距A地30千米
乙距A地80千米
甲
A
乙
B
探究新知
知识点
确定一次函数的表达式
图象表示
(A)
0
4
1
2
3
t/时
s/千米
120
100
80
60
40
20
(B)
可以分别作出两人s 与t 之间的关系图象,找出交点的横坐标就行了.
小明
乙
甲
探究新知
小颖
对于乙,s是t的一次函数,可设s=kt+b.当t=0时,s=100;当t=1时s=80.将它们分别代入s=kt+b中,
可以求出k,b的值,即可以求出乙中s与t之间的函数表达式.你能求出甲的表达式吗?
探究新知
因为甲为正比例函数,设甲的关系式为s=kt,当t=2时s=30,即30=2k,k=15,所以s=15t
小亮
1小时后乙距A地80千米,即乙的速度是20千米/时
2小时后甲距A 地30千米,故甲的速度是15千米/时
设同时出发后t小时相遇,则15t+20t=100,
探究新知
所以
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
小明
小亮
小颖
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
探究新知
探究交流
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
探究新知
例
解:(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组
解得
答:旅客最多可免费携带30千克的行李.
所以当x>30时,y>0.
探究新知
(2)当y=0时, .解得x=30
所以
像这样,先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫做待定系数法.
利用二元一次方程组求一次函数表达式的一般步骤:
1.设:用含字母的系数设出一次函数的表达式:y=kx+b.
2.代:将已知条件代入上述表达式中得k,b的二元一次方程组.
3.解:解这个二元一次方程组得k,b.
4.求:进而求出一次函数的表达式.
探究新知
在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少?
解:设购买量y与单价x的函数解析式为y=kx+b,
因为当x=1000时 y = 800;当x=2000时y = 700,
所以
800k + b = 1000
700k + b = 2000
{
因此,购买量y与单价x的函数解析式为 y =-10x + 9000
当 y = 400时得,-10 x + 900 =400,
所以x =860.
答:当客户购买400kg,单价是860元.
巩固练习
解这个方程组得:
b =900
{
k=-10
解:设这个一次函数的解析式为y=kx+b.
所以这个一次函数的解析式为
-k+b=3,
2k+b=-3,
把点(-1,3)与(2,-3)分别代入,得:
解方程组得
b=1.
k=-2,
y=-2x+1.
探究新知
素养考点 1
已知两点坐标确定一次函数的表达式
已知一次函数的图象过点(-1,3)与(2,-3),
求这个一次函数的解析式.
例
1)设关系式;
2)找x与y的对应值;
3)代入转化成方程(组)
4)解方程(组)确定系数;
5)还原关系式.
探究新知
方法点拨
确定一次函数关系式的方法:
已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
-4k+b=-9,
把点(3,5)与(-4,-9)分别代入,得:
解方程组得
b=-1.
k=2,
所以这个一次函数的解析式为
y=2x-1.
巩固练习
变式训练
(2019?上海)在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是___________.
y=﹣6x+2
连接中考
C
(3,-2)
y=2x+5
课堂检测
基础巩固题
1.若直线 y=0.5x+n 与 y=mx-1 相交于点(1,-2),则( )
A.m=0.5,n=-2.5 B.m=0.5,n=-1
C.m=-1,n=-2.5 D.m=-3,n=-1.5
2.已知二元一次方程组 的解是 在同一平面直角坐标系中,直线y=x﹣5 与直线 y=-x+1 的交点坐标为 .
3.已知函数y=2x+b的图像经过点(a,7)和(-2,a),则这个函数的表达式为____________.
x-y=5
x+y=1
x=3
y=-2
4. 在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.当所挂物体的质量为1kg时,弹簧长度为15cm;当所挂物体的质量为3kg时,弹簧长度为16cm.写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度.
课堂检测
基础巩固题
解:设y与x之间的关系式为y=kx+b.
把(1,15)与(3,16)分别代入,得:
k+b=15,
3k+b=16,
所以y与x之间的关系式为
y=0.5x+14.5
当所挂物体的质量为4kg时,
y=0.5×4+14.5
=16.5,
即弹簧长为16.5cm.
b=14.5.
k=0.5,
解方程组得
温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
课堂检测
能力提升题
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
由已知条件,得
212k + b =100,
32k + b = 0 .
{
课堂检测
能力提升题
解这个方程组,得
所以摄氏温度与华氏温度的函数关系式为
判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
解:设过A,B两点的直线的表达式为y=kx+b.
所以过A,B两点的直线的表达式为y=x-2.
因为当x=4时,y=4-2=2.
所以点C(4,2)在直线y=x-2上.
故三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
课堂检测
拓广探索题
解得
由题意可得,
利用二元一次方程组确定一次函数表达式
用含字母的系数设出一次函数的表达式:y=kx+b
将已知条件代入上述表达式中得关于k,b的二元一次方程组
解这个二元一次方程组得k,b
课堂小结
一次函数表达式
1.二元一次方程组与一次函数有何联系?
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点坐标也是它们所对应的二元一次方程组的解.
2.二元一次方程组有哪些解法?
消元法
图象法
是一种代数方法
导入新知
1. 了解待定系数法,会用二元一次方程组确定一次函数的表达式.
2. 会应用方程与函数的联系解决实际问题.
素养目标
探究 A ,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.1小时后乙距A地80千米; 2小时后甲距A地30千米.
问:经过多长时间两人相遇 ?说出你的方法,并与同学们交流.
1小时后
2小时后甲距A地30千米
乙距A地80千米
甲
A
乙
B
探究新知
知识点
确定一次函数的表达式
图象表示
(A)
0
4
1
2
3
t/时
s/千米
120
100
80
60
40
20
(B)
可以分别作出两人s 与t 之间的关系图象,找出交点的横坐标就行了.
小明
乙
甲
探究新知
小颖
对于乙,s是t的一次函数,可设s=kt+b.当t=0时,s=100;当t=1时s=80.将它们分别代入s=kt+b中,
可以求出k,b的值,即可以求出乙中s与t之间的函数表达式.你能求出甲的表达式吗?
探究新知
因为甲为正比例函数,设甲的关系式为s=kt,当t=2时s=30,即30=2k,k=15,所以s=15t
小亮
1小时后乙距A地80千米,即乙的速度是20千米/时
2小时后甲距A 地30千米,故甲的速度是15千米/时
设同时出发后t小时相遇,则15t+20t=100,
探究新知
所以
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
小明
小亮
小颖
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
探究新知
探究交流
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
探究新知
例
解:(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组
解得
答:旅客最多可免费携带30千克的行李.
所以当x>30时,y>0.
探究新知
(2)当y=0时, .解得x=30
所以
像这样,先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫做待定系数法.
利用二元一次方程组求一次函数表达式的一般步骤:
1.设:用含字母的系数设出一次函数的表达式:y=kx+b.
2.代:将已知条件代入上述表达式中得k,b的二元一次方程组.
3.解:解这个二元一次方程组得k,b.
4.求:进而求出一次函数的表达式.
探究新知
在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少?
解:设购买量y与单价x的函数解析式为y=kx+b,
因为当x=1000时 y = 800;当x=2000时y = 700,
所以
800k + b = 1000
700k + b = 2000
{
因此,购买量y与单价x的函数解析式为 y =-10x + 9000
当 y = 400时得,-10 x + 900 =400,
所以x =860.
答:当客户购买400kg,单价是860元.
巩固练习
解这个方程组得:
b =900
{
k=-10
解:设这个一次函数的解析式为y=kx+b.
所以这个一次函数的解析式为
-k+b=3,
2k+b=-3,
把点(-1,3)与(2,-3)分别代入,得:
解方程组得
b=1.
k=-2,
y=-2x+1.
探究新知
素养考点 1
已知两点坐标确定一次函数的表达式
已知一次函数的图象过点(-1,3)与(2,-3),
求这个一次函数的解析式.
例
1)设关系式;
2)找x与y的对应值;
3)代入转化成方程(组)
4)解方程(组)确定系数;
5)还原关系式.
探究新知
方法点拨
确定一次函数关系式的方法:
已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
-4k+b=-9,
把点(3,5)与(-4,-9)分别代入,得:
解方程组得
b=-1.
k=2,
所以这个一次函数的解析式为
y=2x-1.
巩固练习
变式训练
(2019?上海)在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是___________.
y=﹣6x+2
连接中考
C
(3,-2)
y=2x+5
课堂检测
基础巩固题
1.若直线 y=0.5x+n 与 y=mx-1 相交于点(1,-2),则( )
A.m=0.5,n=-2.5 B.m=0.5,n=-1
C.m=-1,n=-2.5 D.m=-3,n=-1.5
2.已知二元一次方程组 的解是 在同一平面直角坐标系中,直线y=x﹣5 与直线 y=-x+1 的交点坐标为 .
3.已知函数y=2x+b的图像经过点(a,7)和(-2,a),则这个函数的表达式为____________.
x-y=5
x+y=1
x=3
y=-2
4. 在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.当所挂物体的质量为1kg时,弹簧长度为15cm;当所挂物体的质量为3kg时,弹簧长度为16cm.写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度.
课堂检测
基础巩固题
解:设y与x之间的关系式为y=kx+b.
把(1,15)与(3,16)分别代入,得:
k+b=15,
3k+b=16,
所以y与x之间的关系式为
y=0.5x+14.5
当所挂物体的质量为4kg时,
y=0.5×4+14.5
=16.5,
即弹簧长为16.5cm.
b=14.5.
k=0.5,
解方程组得
温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
课堂检测
能力提升题
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
由已知条件,得
212k + b =100,
32k + b = 0 .
{
课堂检测
能力提升题
解这个方程组,得
所以摄氏温度与华氏温度的函数关系式为
判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
解:设过A,B两点的直线的表达式为y=kx+b.
所以过A,B两点的直线的表达式为y=x-2.
因为当x=4时,y=4-2=2.
所以点C(4,2)在直线y=x-2上.
故三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
课堂检测
拓广探索题
解得
由题意可得,
利用二元一次方程组确定一次函数表达式
用含字母的系数设出一次函数的表达式:y=kx+b
将已知条件代入上述表达式中得关于k,b的二元一次方程组
解这个二元一次方程组得k,b
课堂小结
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
