人教版八年级数学上册14.1.1同底数幂的乘法教学课件 (共19张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.1.1同底数幂的乘法教学课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 600.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 13:59:45 | ||
图片预览





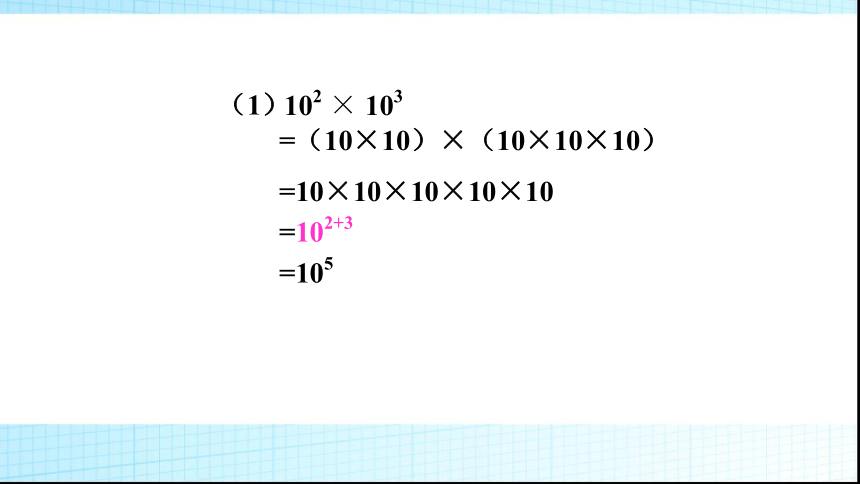
文档简介
(共19张PPT)
14.1.1同底数幂的乘法
教学目标
1.熟记同底数幂乘法的法则,能正确的运用同底数幂乘法的运算性质解决问题。
2.通过推导过程培养观察、发现、归纳、概括、猜想等探究能力。
教学重难点
重点:理解同底数幂的运算法则并会运用。
难点:会运用同底数幂的运算法则解决问题。
一年以3×10
秒计算,比邻星与地球的距离约
为多少千米?
7
问题:光在真空中的速度大约是3×10
千米/秒,
太阳系以外距离地球最近的恒星是比邻星,它发出
的光到达地球大约需要4.22年。
5
3x105x4.22x3x107
=37.98X(108X107)
108X107等于多少呢?
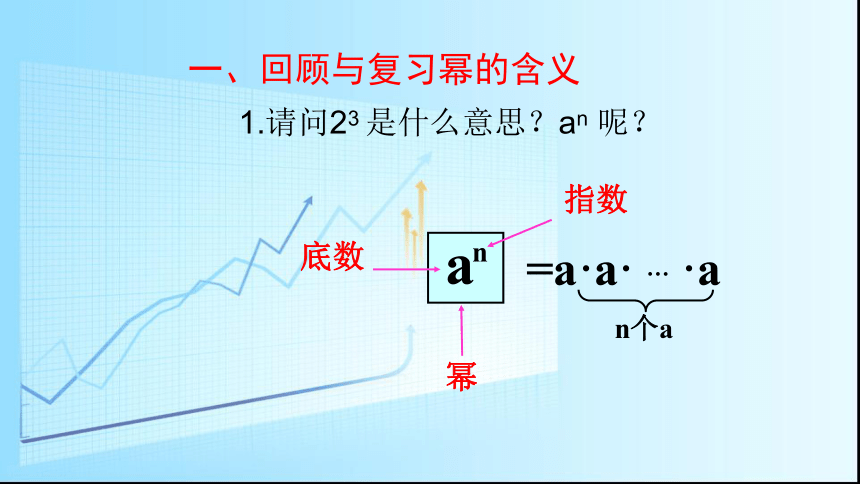
一、回顾与复习幂的含义
a
n
指数
幂
=a·a·
…
·a
n个a
底数
1.请问23
是什么意思?an
呢?
2.练习
(1)请指出下列各式的底数和指数
34
a3
(a+b)2
(-2)3
-23
(2)思考
(-2)3
与-23的含义是否相同,结果是否相等?
(-2)4与
-24的含义是否相同,结果是否相等?
二、互动新授
探究活动一:以10为底的同底数幂乘法的运算
1.出示教材P2“做一做”
计算下列各式:
(1)102×103
(2)105×108
你发现了什么?
=(10×10)×(10×10×10)
=10×10×10×10×10
=105
102
×
103
(1)
=102+3
=(10×10×···×10)×(10×10×···×10)
5个10
8个10
=10×10×···×10
13个10
=10
13
10
×
10
5
8
(2)
=105+8
=(10×10×···×10)×(10×10×···×10)
m个10
n个10
=10×10×···×10
(m+n)个10
=10
m+n
10
×
10
m
n
2、拓展问题
你能计算
吗?请写出过程和结果
10
×
10
m
n
探究活动二:
以a为底数的同底数幂的乘法运算
(1)a3·a2
(2)2m×2n等于什么?
(3)
(a+b)m×(a+b)n
呢?
(m,n
都是正整数)
=2m+n
=(2×2×···×2)×(2×2×···×2)
m个2
n个2
2m×2n
=
=
m个
n个
(3)
(1)a3·a2=(a·a·a)
·(a·a)=a·a·a·a·a=a5
(a+b)m×(a+b)n
(a+b)×···
×(a+b)
×
(2)
(a+b)×
···
×(a+b)
(a+b)m+n
探究活动三:
同底数幂的乘法运算法则
1、如果m,n都是正整数,那么am
·
an等于什么?
请同学们讨论一下,然后写出推导过程
am
·
an
=(a·a·
…
·a)·(a·a·
…
·a)
m个a
n个a
=a·a·
…
·a
(m+n)个a
=am+n
am
·
an
=am+n(m,n都是正整数)
同底数幂相乘
底数
,
指数
.
不变
相加
2、剖析运算法则,加深学生对运算法则理解
①等号左边是什么运算?
②等号两边的底数有什么关系?
③等号两边的指数有什么关系?
④公式中的底数a可以表示什么数?
例1.
计算:
(1)
(-3)7×(-3)6
;
(2)
-x3·x5;
(3)
b2m·b2m+1.
解:(1)
(-3)7×(-3)6=(-3)7+6=(-3)13
(2)-x3·
x5
=
-x3+5
=
-x8
(3)
b2m·
b2m+1
=
b2m+2m+1=
b4m+1
探究活动四:同底数幂乘法运算的应用
想一想
am
·
an
·
ap
等于什么?
am·
an·
ap
=
am+n+p
计算:
(1)x10
·
x
(2)10×102×104
(3)-a2
·
a6
(4)
(-x)
·
x2
·
(-x)4
解:
(1)x10
·x
=
x10+1=
x11
(2)10×102×104
=101+2+4
=107
(3)
-a2
·
a6
=-a8
(4)
(-x)
·
x2
·
(-x)4=-x7
三、挑战勇气
一年以3×10
秒计算,比邻星与地球的距离约
为多少千米?
7
问题:光在真空中的速度大约是3×10
千米/秒,
太阳系以外距离地球最近的恒星是比邻星,它发出
的光到达地球大约需要4.22年。
5
3x105x4.22x3x107
=37.98X(108X107)
108X107等于多少呢?
四、课堂小结
今天我们学到了什么?
再 见
14.1.1同底数幂的乘法
教学目标
1.熟记同底数幂乘法的法则,能正确的运用同底数幂乘法的运算性质解决问题。
2.通过推导过程培养观察、发现、归纳、概括、猜想等探究能力。
教学重难点
重点:理解同底数幂的运算法则并会运用。
难点:会运用同底数幂的运算法则解决问题。
一年以3×10
秒计算,比邻星与地球的距离约
为多少千米?
7
问题:光在真空中的速度大约是3×10
千米/秒,
太阳系以外距离地球最近的恒星是比邻星,它发出
的光到达地球大约需要4.22年。
5
3x105x4.22x3x107
=37.98X(108X107)
108X107等于多少呢?
一、回顾与复习幂的含义
a
n
指数
幂
=a·a·
…
·a
n个a
底数
1.请问23
是什么意思?an
呢?
2.练习
(1)请指出下列各式的底数和指数
34
a3
(a+b)2
(-2)3
-23
(2)思考
(-2)3
与-23的含义是否相同,结果是否相等?
(-2)4与
-24的含义是否相同,结果是否相等?
二、互动新授
探究活动一:以10为底的同底数幂乘法的运算
1.出示教材P2“做一做”
计算下列各式:
(1)102×103
(2)105×108
你发现了什么?
=(10×10)×(10×10×10)
=10×10×10×10×10
=105
102
×
103
(1)
=102+3
=(10×10×···×10)×(10×10×···×10)
5个10
8个10
=10×10×···×10
13个10
=10
13
10
×
10
5
8
(2)
=105+8
=(10×10×···×10)×(10×10×···×10)
m个10
n个10
=10×10×···×10
(m+n)个10
=10
m+n
10
×
10
m
n
2、拓展问题
你能计算
吗?请写出过程和结果
10
×
10
m
n
探究活动二:
以a为底数的同底数幂的乘法运算
(1)a3·a2
(2)2m×2n等于什么?
(3)
(a+b)m×(a+b)n
呢?
(m,n
都是正整数)
=2m+n
=(2×2×···×2)×(2×2×···×2)
m个2
n个2
2m×2n
=
=
m个
n个
(3)
(1)a3·a2=(a·a·a)
·(a·a)=a·a·a·a·a=a5
(a+b)m×(a+b)n
(a+b)×···
×(a+b)
×
(2)
(a+b)×
···
×(a+b)
(a+b)m+n
探究活动三:
同底数幂的乘法运算法则
1、如果m,n都是正整数,那么am
·
an等于什么?
请同学们讨论一下,然后写出推导过程
am
·
an
=(a·a·
…
·a)·(a·a·
…
·a)
m个a
n个a
=a·a·
…
·a
(m+n)个a
=am+n
am
·
an
=am+n(m,n都是正整数)
同底数幂相乘
底数
,
指数
.
不变
相加
2、剖析运算法则,加深学生对运算法则理解
①等号左边是什么运算?
②等号两边的底数有什么关系?
③等号两边的指数有什么关系?
④公式中的底数a可以表示什么数?
例1.
计算:
(1)
(-3)7×(-3)6
;
(2)
-x3·x5;
(3)
b2m·b2m+1.
解:(1)
(-3)7×(-3)6=(-3)7+6=(-3)13
(2)-x3·
x5
=
-x3+5
=
-x8
(3)
b2m·
b2m+1
=
b2m+2m+1=
b4m+1
探究活动四:同底数幂乘法运算的应用
想一想
am
·
an
·
ap
等于什么?
am·
an·
ap
=
am+n+p
计算:
(1)x10
·
x
(2)10×102×104
(3)-a2
·
a6
(4)
(-x)
·
x2
·
(-x)4
解:
(1)x10
·x
=
x10+1=
x11
(2)10×102×104
=101+2+4
=107
(3)
-a2
·
a6
=-a8
(4)
(-x)
·
x2
·
(-x)4=-x7
三、挑战勇气
一年以3×10
秒计算,比邻星与地球的距离约
为多少千米?
7
问题:光在真空中的速度大约是3×10
千米/秒,
太阳系以外距离地球最近的恒星是比邻星,它发出
的光到达地球大约需要4.22年。
5
3x105x4.22x3x107
=37.98X(108X107)
108X107等于多少呢?
四、课堂小结
今天我们学到了什么?
再 见
