22.1一元二次方程-华东师大版九年级数学上册课件(共17张PPT)
文档属性
| 名称 | 22.1一元二次方程-华东师大版九年级数学上册课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 707.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第22章
一元二次方程
§22.1一元二次方程
知识回顾
1、观察方程:
2x=1;
3x+2=x-4;
2(x+2)-3(x-1)=0
它们都含有
个未知数,并且未知数的最高次数是
,这样的整式方程叫做一元一次方程.
2、下列方程哪些是一元一次方程
____________
(1)5x+3=0
(2)2x+y=3
(3)
(4)
x2-2x+1=0
(5)
(1)、
一
1次
(3)
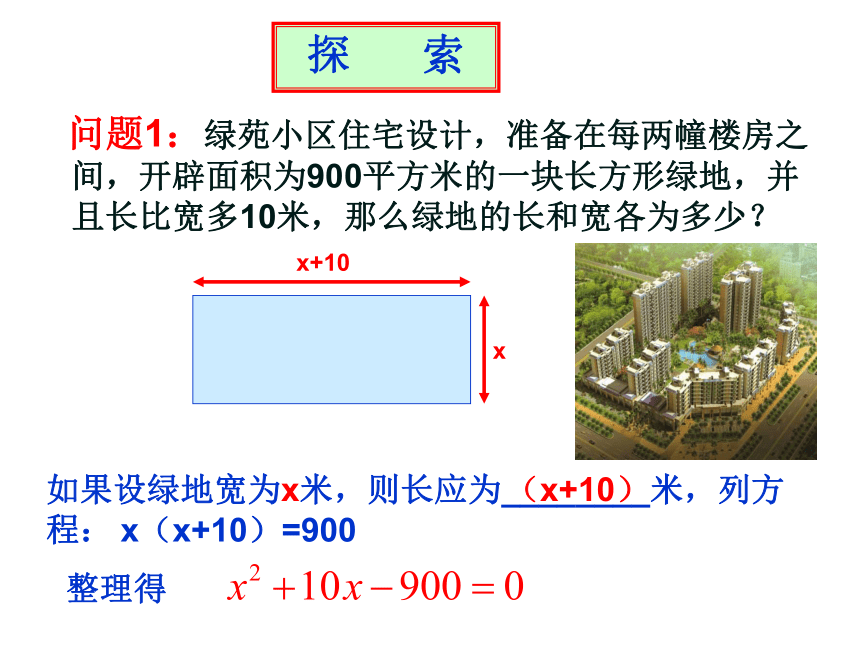
问题1:绿苑小区住宅设计,准备在每两幢楼房之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少?
探
索
如果设绿地宽为x米,则长应为________米,列方程:
(x+10)
x
x+10
x(x+10)=900
整理得
问题2:学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册。求这两年的年平均增长率。
设则两年的年平均增长率为x。则:
去年图书册数:_____万册,
今年图书册数:_____________万册,
明年图书册数:_____________________万册。
5
5+5x=5(1+x)
列方程,得
整理得
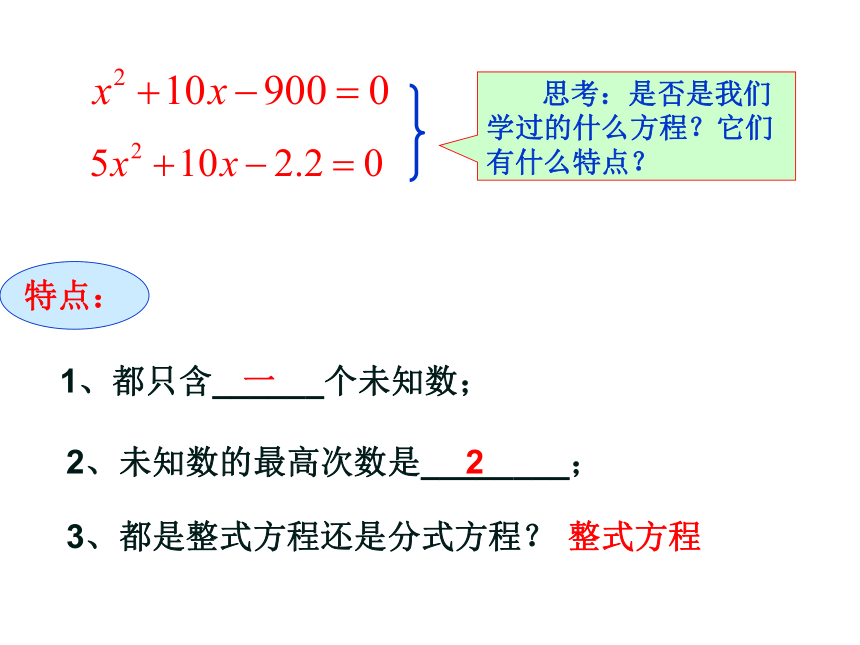
思考:是否是我们学过的什么方程?它们有什么特点?
特点:
1、都只含______个未知数;
一
2、未知数的最高次数是________;
2
3、都是整式方程还是分式方程?
整式方程
概
括
知识点1
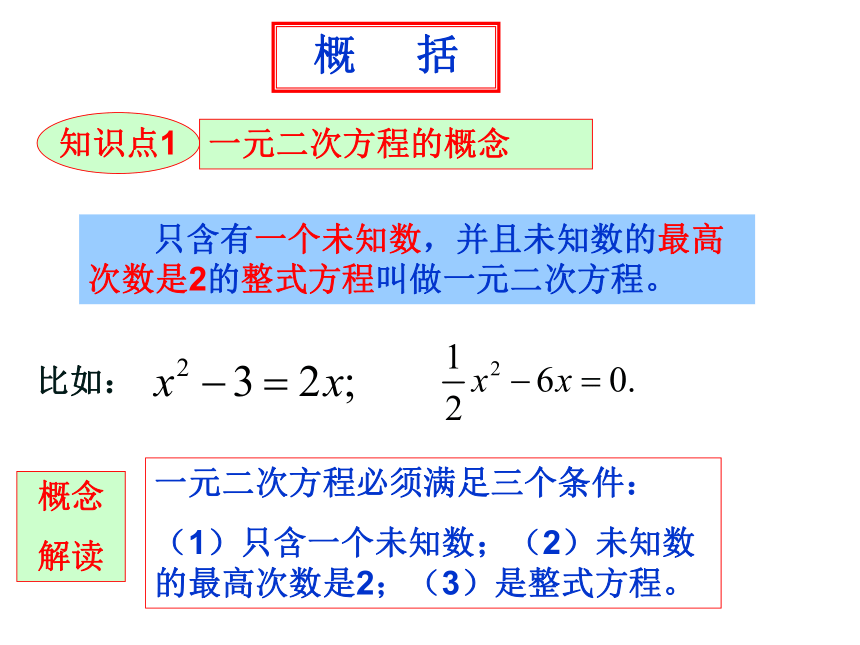
一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
比如:
概念
解读
一元二次方程必须满足三个条件:
(1)只含一个未知数;(2)未知数的最高次数是2;(3)是整式方程。
尝试练习
一个微信群里共有x个好友,每个好友都分别给其他好友发了一条消息,这样一共产生56条消息.那么该微信群中有多少好友在线?(只列方程,不求解)
解:由题意,得
x(x-1)=56
归
纳
建立一元二次方程模型解决实际问题时,既要利用题目条件中给出的等量关系,又要抓住题目中隐含的一些常用关系式(如面积公式、体积公式、利润公式等)进行列方程.
(2)
列一元二次方程的一般步骤:①审题,找未知量与已知量;②设合适的未知数;③找等量关系;④列一元二次方程.
知识点2
一元二次方程的一般形式
任何一个一元二次方程都可以整理成如下形式:
一元二次方程的一般形式是:
其中
分别叫做二次项和一次项;a、b、c
分别叫做二次项系数、一次项系数和常数项。
一般式
解读
确定一元二次方程各项系数时,先要化为一般式;各项系数包括前面的符号。
尝试练习
1、下列方程:
一定是一元二次方程的是______________.
(3)
(4)
学法
总结
判断一元二次方程时,要从原方程及整理后的方程两方面进行判断,看其是否符合一元二次方程的条件.除满足三个条件外,特别注意二次项系数不能为0.
2、(课本P19)将下列一元二次方程化为一般形式,并指出方程的二次项系数、一次项系数和常数项:
解:
3,-1,-2.
-2,7,-3.
2,-7,3.
-1,5,0.
-1,-2,-11.
解:
解:
解:
例1
【解】
由题意,得
m+1≠0
解得m=1
已知
是关于x的
一元二次方程,求m的值。
特别注意:一元二次方程二次项系数不为0
1、已知方程
是关于x的一元二次方程,则m的取值范围是________.
m≠3
2、关于x的方程
是一元二次方程,则m的值是(
)
C
对应练习
3、已知
是关于x的方程,问:
(1)当m为何值时,它是一元二次方程?
(2)当m为何值时,它是一元一次方程?
【解】
(1)由题意,得
∴m≠±2
(2)由题意,得
解得m
=2
学法
总结
例2
(1)已知关于x的方程
的一个根为x=3,则实数k的值为(
)
A.1
B.-1
C.2
D.-2
A
(2)已知x=1是一元二次方程
的一个根,则代数式
的值为________.
1
学法
总结
方程的解满足方程,将解代入方程可求待定的系数。
定义:能使一元二次方程左右两边相等的未知数的值叫做
一元二次方程的根(解).
知识点3
一元二次方程的根的定义
1、若关于x的一元二次方程
的解是x=1,则2013-a-b的值是(
)
A.2018
B.2008
C.2014
D.2012
B
A
2、已知m是方程x2﹣2x﹣1=0的一个根,则代数式2m2﹣4m+2017的值为( )
A.2019
B.2018
C.2016
D.2015
A
3、关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1
B.﹣1
C.1或﹣1
D.
4、若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )
A.1
B.2
C.﹣1
D.﹣2
D
对应练习
课堂小结
这节课你学会了
1.一元二次方程的定义:
①含一个未知数;②并且未知数的最高次数是2;③整式方程。
2、一元二次方程的一般形式:
3、一元二次方程的根的定义
第22章
一元二次方程
§22.1一元二次方程
知识回顾
1、观察方程:
2x=1;
3x+2=x-4;
2(x+2)-3(x-1)=0
它们都含有
个未知数,并且未知数的最高次数是
,这样的整式方程叫做一元一次方程.
2、下列方程哪些是一元一次方程
____________
(1)5x+3=0
(2)2x+y=3
(3)
(4)
x2-2x+1=0
(5)
(1)、
一
1次
(3)
问题1:绿苑小区住宅设计,准备在每两幢楼房之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少?
探
索
如果设绿地宽为x米,则长应为________米,列方程:
(x+10)
x
x+10
x(x+10)=900
整理得
问题2:学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册。求这两年的年平均增长率。
设则两年的年平均增长率为x。则:
去年图书册数:_____万册,
今年图书册数:_____________万册,
明年图书册数:_____________________万册。
5
5+5x=5(1+x)
列方程,得
整理得
思考:是否是我们学过的什么方程?它们有什么特点?
特点:
1、都只含______个未知数;
一
2、未知数的最高次数是________;
2
3、都是整式方程还是分式方程?
整式方程
概
括
知识点1
一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
比如:
概念
解读
一元二次方程必须满足三个条件:
(1)只含一个未知数;(2)未知数的最高次数是2;(3)是整式方程。
尝试练习
一个微信群里共有x个好友,每个好友都分别给其他好友发了一条消息,这样一共产生56条消息.那么该微信群中有多少好友在线?(只列方程,不求解)
解:由题意,得
x(x-1)=56
归
纳
建立一元二次方程模型解决实际问题时,既要利用题目条件中给出的等量关系,又要抓住题目中隐含的一些常用关系式(如面积公式、体积公式、利润公式等)进行列方程.
(2)
列一元二次方程的一般步骤:①审题,找未知量与已知量;②设合适的未知数;③找等量关系;④列一元二次方程.
知识点2
一元二次方程的一般形式
任何一个一元二次方程都可以整理成如下形式:
一元二次方程的一般形式是:
其中
分别叫做二次项和一次项;a、b、c
分别叫做二次项系数、一次项系数和常数项。
一般式
解读
确定一元二次方程各项系数时,先要化为一般式;各项系数包括前面的符号。
尝试练习
1、下列方程:
一定是一元二次方程的是______________.
(3)
(4)
学法
总结
判断一元二次方程时,要从原方程及整理后的方程两方面进行判断,看其是否符合一元二次方程的条件.除满足三个条件外,特别注意二次项系数不能为0.
2、(课本P19)将下列一元二次方程化为一般形式,并指出方程的二次项系数、一次项系数和常数项:
解:
3,-1,-2.
-2,7,-3.
2,-7,3.
-1,5,0.
-1,-2,-11.
解:
解:
解:
例1
【解】
由题意,得
m+1≠0
解得m=1
已知
是关于x的
一元二次方程,求m的值。
特别注意:一元二次方程二次项系数不为0
1、已知方程
是关于x的一元二次方程,则m的取值范围是________.
m≠3
2、关于x的方程
是一元二次方程,则m的值是(
)
C
对应练习
3、已知
是关于x的方程,问:
(1)当m为何值时,它是一元二次方程?
(2)当m为何值时,它是一元一次方程?
【解】
(1)由题意,得
∴m≠±2
(2)由题意,得
解得m
=2
学法
总结
例2
(1)已知关于x的方程
的一个根为x=3,则实数k的值为(
)
A.1
B.-1
C.2
D.-2
A
(2)已知x=1是一元二次方程
的一个根,则代数式
的值为________.
1
学法
总结
方程的解满足方程,将解代入方程可求待定的系数。
定义:能使一元二次方程左右两边相等的未知数的值叫做
一元二次方程的根(解).
知识点3
一元二次方程的根的定义
1、若关于x的一元二次方程
的解是x=1,则2013-a-b的值是(
)
A.2018
B.2008
C.2014
D.2012
B
A
2、已知m是方程x2﹣2x﹣1=0的一个根,则代数式2m2﹣4m+2017的值为( )
A.2019
B.2018
C.2016
D.2015
A
3、关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1
B.﹣1
C.1或﹣1
D.
4、若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )
A.1
B.2
C.﹣1
D.﹣2
D
对应练习
课堂小结
这节课你学会了
1.一元二次方程的定义:
①含一个未知数;②并且未知数的最高次数是2;③整式方程。
2、一元二次方程的一般形式:
3、一元二次方程的根的定义
