第十七章特殊三角形达标测试卷-2020秋冀教版(河北)八年级数学上册(Word版 含答案)
文档属性
| 名称 | 第十七章特殊三角形达标测试卷-2020秋冀教版(河北)八年级数学上册(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览




文档简介
第十七章达标测试卷
一、选择题(1~10小题各3分,11~16小题各2分,共42分)
1.一个等腰三角形的两边长分别为6和12,则这个等腰三角形的周长为( )
A.18
B.24
C.30
D.24或30
2.等腰三角形的一个角为70°,则这个等腰三角形的顶角为( )
A.70°
B.55°
C.40°
D.40°或70°
3.如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明Rt△DEC≌Rt△BFA,则需添加的条件是( )
A.EC=FA
B.DC=BA
C.∠D=∠B
D.∠DCE=∠BAF
(第3题)
(第5题)
4.下列各组长度的线段能构成直角三角形的是( )
A.30,40,50
B.7,12,13
C.5,9,12
D.3,4,6
5.如图,在等边三角形ABC中,AB=10
cm,D是AB的中点,过点D作DE⊥AC于点E,则EC的长是( )
A.2.5
cm
B.5
cm
C.7
cm
D.7.5
cm
6.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40
n
mile的速度向正北方向航行,2
h后到达灯塔P的北偏东40°方向的N处,则N处与灯塔P的距离为( )
A.40
n
mile
B.60
n
mile
C.70
n
mile
D.80
n
mile
(第6题)
(第7题)
7.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC与∠ACB的平分线,BD,CE相交于点F,则图中的等腰三角形有( )
A.6个
B.7个
C.8个
D.9个
8.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB的中点.沿过点E的直线折叠,使点B与点A重合,折痕EF交BC于点F.已知EF=,则BC的长是( )
A.
B.3
C.3
D.3
(第8题)
(第9题)
(第10题)
9.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为( )
A.40°
B.45°
C.55°
D.70°
10.如图,在钝角三角形ABC中,∠ABC为钝角,先以点B为圆心,AB长为半径画弧,再以点C为圆心,AC长为半径画弧.两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD
B.CE平分∠ACD
C.△ABD是等腰三角形
D.△ACD是等边三角形
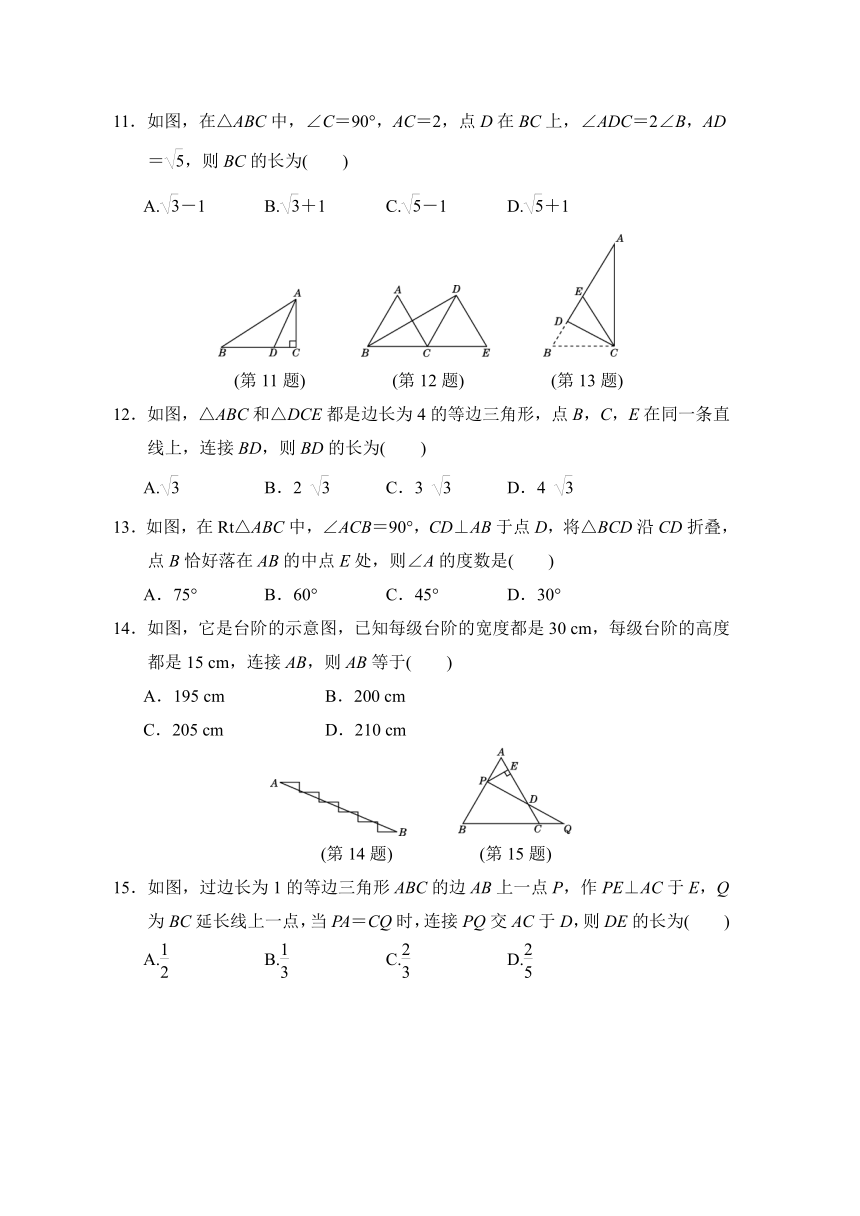
11.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.-1
B.+1
C.-1
D.+1
(第11题)
(第12题)
(第13题)
12.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为( )
A.
B.2
C.3
D.4
13.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,将△BCD沿CD折叠,点B恰好落在AB的中点E处,则∠A的度数是( )
A.75°
B.60°
C.45°
D.30°
14.如图,它是台阶的示意图,已知每级台阶的宽度都是30
cm,每级台阶的高度都是15
cm,连接AB,则AB等于( )
A.195
cm
B.200
cm
C.205
cm
D.210
cm
(第14题)
(第15题)
15.如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC于D,则DE的长为( )
A.
B.
C.
D.
16.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下四个结论:①AE=CF;②△PEF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A,B重合),上述结论中始终正确的有( )
A.1个
B.2个
C.3个
D.4个
(第16题)
(第19题)
二、填空题(17小题3分,18,19小题每空2分,共11分)
17.用反证法证明“a>b”时,应先假设________.
18.观察下列几组勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…,按此规律,当直角三角形的较短直角边长是11时,较长直角边长是________;当直角三角形的较短直角边长是2n+1时,较长直角边长是________.
19.如图,在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D,交AB于E.若AC=6
cm,则∠ADE=________,AD=________cm.
三、解答题(20小题8分,21~23小题各9分,24,25小题各10分,26小题12分,共67分)
20.如图,在△ABC中,CD⊥AB于D,AB=AC=13,BD=1.求:
(1)CD的长;
(2)BC的长.
(第20题)
21.如图,在△ABC中,∠C=90°,且AC=BC,AD平分∠BAC,交BC于点D,DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若AB=6
cm,求△BDE的周长.
(第21题)
22.如图,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
(第22题)
23.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于点E.
(1)求证:AD=CD;
(2)求AE的长.
(第23题)
24.如图,OA⊥OB,OA=45
cm,OB=15
cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
(第24题)
25.如图,△ABC是边长为3
cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速运动,它们的速度都是1
cm/s,当点P到达点B时,P,Q两点停止运动.设点P的运动时间为t
s,则当t为何值时,△PBQ是直角三角形?
(第25题)
26.如图①,在等腰直角三角形BCD中,∠BDC=90°,
BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF.
(1)求证:△FBD≌△ACD.
(2)延长BF交AC于点E,且BE⊥AC,求证:CE=BF.
(3)在(2)的条件下,H是BC边的中点,连接DH,与BE相交于点G,如图②.
试探索CE,GE,BG之间的数量关系,并证明你的结论.
(第26题)
答案
一、1.C 2.D 3.B 4.A 5.D 6.D
7.C 8.B
9.C 点拨:∵AC=CB,∠C=40°,
∴∠BAC=∠B=×(180°-40°)=70°,
∵AD=AE,∴∠ADE=∠AED=×(180°-70°)=55°,
∵GH∥DE,
∴∠GAD=∠ADE=55°.
10.D
11.D 点拨:∵∠ADC=2∠B,∠ADC=∠B+∠BAD,
∴∠B=∠DAB,
∴DB=DA=.
在Rt△ADC中,
DC===1,
∴BC=+1.故选D.
12.D 13.D 14.A
15.A 点拨:如图,过P作PF∥BC,PF交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
∵在△PFD和△QCD中,
∴△PFD≌△QCD,
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,
∴AE+CD=DE=AC,
∵AC=1,
∴DE=.
(第15题)
16.C
二、17.a≤b 18.60;2n2+2n
19.60°;2
三、20.解:(1)∵AB=13,BD=1,
∴AD=13-1=12.
在Rt△ACD中,CD===5.
(2)在Rt△BCD中,BC===.
21.(1)证明:∵AD平分∠CAB,AC⊥BC于点C,DE⊥AB于点E,
∴CD=DE.
在Rt△ACD与Rt△AED中,
∴Rt△ACD≌Rt△AED.
即△ACD≌△AED.
(2)解:由(1)知△ACD≌△AED,
∴AC=AE.
又∵AC=BC,
∴BC=AE,
∴△BDE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AE+EB=AB=6
cm.
22.(1)证明:∵AB=AC,
∴∠B=∠C.
在△DBE和△ECF中,
∴△DBE≌△ECF.
∴DE=EF.
∴△DEF是等腰三角形.
(2)解:由(1)可知△DBE≌△ECF,∴∠BDE=∠CEF.
∵∠A+∠B+∠C=180°,∠A=40°,
∠B=∠C,
∴∠B=×(180°-40°)=70°.
∴∠BDE+∠BED=110°.
∴∠CEF+∠BED=110°.
∴∠DEF=70°.
23.(1)证明:如图,过点D作DM⊥AB,DN⊥BF,垂足分别为M,N.
(第23题)
∵BD平分∠ABF,
∴DM=DN.
∵∠ADC=45°=∠ABC,
∴∠BAD=∠BCD.
又∵∠DMA=∠DNC=90°,
∴△ADM≌△CDN.
∴AD=CD.
(2)解:∵AD=CD,∠ADC=45°,
∴∠CAD=∠ACE=67.5°.
又∵∠CAB=45°,
∴∠AEC=67.5°.
∴∠ACE=∠AEC.
∴AE=AC=4.
24.解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,
∴BC=CA.
设BC=CA=x
cm,则OC=(45-x)cm,由勾股定理可知OB2+OC2=BC2,即152+(45-x)2=x2,解得x=25.
答:机器人行走的路程BC是25
cm.
25.解:根据题意,得AP=BQ=t
cm.
在△ABC中,AB=3
cm,∠B=60°,
∴BP=(3-t)cm.
若△PBQ是直角三角形,
则∠BQP=90°或∠BPQ=90°.
当∠BQP=90°时,BQ=BP,
即t=(3-t),
解得t=1;
当∠BPQ=90°时,BP=BQ,
即3-t=t,
解得t=2.
综上,当t=1或t=2时,△PBQ是直角三角形.
26.(1)证明:∵△BCD是等腰直角三角形,且∠BDC=90°,∴BD=CD,∠BDC=∠CDA=90°.
在△FBD和△ACD中,
∴△FBD≌△ACD(SAS).
(2)证明:∵BE⊥AC,
∴∠BEA=∠BEC=90°.
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE=BE,
∴△ABE≌△CBE(ASA),
∴AE=CE.∴CE=AC.
由(1)知△FBD≌△ACD,
∴BF=CA,∴CE=BF.
(3)解:BG2=GE2+CE2.证明如下:连接CG,∵H是BC边的中点,BD=CD,
∴HD垂直平分BC,∴BG=CG(线段垂直平分线上的点到这条线段两个端点的距离相等).∵BE⊥AC,
∴在Rt△CEG中,CG2=GE2+CE2,∴BG2=GE2+CE2.
点拨:本题综合考查全等三角形的判定与性质及通过添加辅助线利用勾股定理解决问题.
一、选择题(1~10小题各3分,11~16小题各2分,共42分)
1.一个等腰三角形的两边长分别为6和12,则这个等腰三角形的周长为( )
A.18
B.24
C.30
D.24或30
2.等腰三角形的一个角为70°,则这个等腰三角形的顶角为( )
A.70°
B.55°
C.40°
D.40°或70°
3.如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明Rt△DEC≌Rt△BFA,则需添加的条件是( )
A.EC=FA
B.DC=BA
C.∠D=∠B
D.∠DCE=∠BAF
(第3题)
(第5题)
4.下列各组长度的线段能构成直角三角形的是( )
A.30,40,50
B.7,12,13
C.5,9,12
D.3,4,6
5.如图,在等边三角形ABC中,AB=10
cm,D是AB的中点,过点D作DE⊥AC于点E,则EC的长是( )
A.2.5
cm
B.5
cm
C.7
cm
D.7.5
cm
6.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40
n
mile的速度向正北方向航行,2
h后到达灯塔P的北偏东40°方向的N处,则N处与灯塔P的距离为( )
A.40
n
mile
B.60
n
mile
C.70
n
mile
D.80
n
mile
(第6题)
(第7题)
7.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC与∠ACB的平分线,BD,CE相交于点F,则图中的等腰三角形有( )
A.6个
B.7个
C.8个
D.9个
8.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB的中点.沿过点E的直线折叠,使点B与点A重合,折痕EF交BC于点F.已知EF=,则BC的长是( )
A.
B.3
C.3
D.3
(第8题)
(第9题)
(第10题)
9.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为( )
A.40°
B.45°
C.55°
D.70°
10.如图,在钝角三角形ABC中,∠ABC为钝角,先以点B为圆心,AB长为半径画弧,再以点C为圆心,AC长为半径画弧.两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD
B.CE平分∠ACD
C.△ABD是等腰三角形
D.△ACD是等边三角形
11.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.-1
B.+1
C.-1
D.+1
(第11题)
(第12题)
(第13题)
12.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为( )
A.
B.2
C.3
D.4
13.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,将△BCD沿CD折叠,点B恰好落在AB的中点E处,则∠A的度数是( )
A.75°
B.60°
C.45°
D.30°
14.如图,它是台阶的示意图,已知每级台阶的宽度都是30
cm,每级台阶的高度都是15
cm,连接AB,则AB等于( )
A.195
cm
B.200
cm
C.205
cm
D.210
cm
(第14题)
(第15题)
15.如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC于D,则DE的长为( )
A.
B.
C.
D.
16.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下四个结论:①AE=CF;②△PEF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A,B重合),上述结论中始终正确的有( )
A.1个
B.2个
C.3个
D.4个
(第16题)
(第19题)
二、填空题(17小题3分,18,19小题每空2分,共11分)
17.用反证法证明“a>b”时,应先假设________.
18.观察下列几组勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…,按此规律,当直角三角形的较短直角边长是11时,较长直角边长是________;当直角三角形的较短直角边长是2n+1时,较长直角边长是________.
19.如图,在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D,交AB于E.若AC=6
cm,则∠ADE=________,AD=________cm.
三、解答题(20小题8分,21~23小题各9分,24,25小题各10分,26小题12分,共67分)
20.如图,在△ABC中,CD⊥AB于D,AB=AC=13,BD=1.求:
(1)CD的长;
(2)BC的长.
(第20题)
21.如图,在△ABC中,∠C=90°,且AC=BC,AD平分∠BAC,交BC于点D,DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若AB=6
cm,求△BDE的周长.
(第21题)
22.如图,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
(第22题)
23.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于点E.
(1)求证:AD=CD;
(2)求AE的长.
(第23题)
24.如图,OA⊥OB,OA=45
cm,OB=15
cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
(第24题)
25.如图,△ABC是边长为3
cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速运动,它们的速度都是1
cm/s,当点P到达点B时,P,Q两点停止运动.设点P的运动时间为t
s,则当t为何值时,△PBQ是直角三角形?
(第25题)
26.如图①,在等腰直角三角形BCD中,∠BDC=90°,
BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF.
(1)求证:△FBD≌△ACD.
(2)延长BF交AC于点E,且BE⊥AC,求证:CE=BF.
(3)在(2)的条件下,H是BC边的中点,连接DH,与BE相交于点G,如图②.
试探索CE,GE,BG之间的数量关系,并证明你的结论.
(第26题)
答案
一、1.C 2.D 3.B 4.A 5.D 6.D
7.C 8.B
9.C 点拨:∵AC=CB,∠C=40°,
∴∠BAC=∠B=×(180°-40°)=70°,
∵AD=AE,∴∠ADE=∠AED=×(180°-70°)=55°,
∵GH∥DE,
∴∠GAD=∠ADE=55°.
10.D
11.D 点拨:∵∠ADC=2∠B,∠ADC=∠B+∠BAD,
∴∠B=∠DAB,
∴DB=DA=.
在Rt△ADC中,
DC===1,
∴BC=+1.故选D.
12.D 13.D 14.A
15.A 点拨:如图,过P作PF∥BC,PF交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
∵在△PFD和△QCD中,
∴△PFD≌△QCD,
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,
∴AE+CD=DE=AC,
∵AC=1,
∴DE=.
(第15题)
16.C
二、17.a≤b 18.60;2n2+2n
19.60°;2
三、20.解:(1)∵AB=13,BD=1,
∴AD=13-1=12.
在Rt△ACD中,CD===5.
(2)在Rt△BCD中,BC===.
21.(1)证明:∵AD平分∠CAB,AC⊥BC于点C,DE⊥AB于点E,
∴CD=DE.
在Rt△ACD与Rt△AED中,
∴Rt△ACD≌Rt△AED.
即△ACD≌△AED.
(2)解:由(1)知△ACD≌△AED,
∴AC=AE.
又∵AC=BC,
∴BC=AE,
∴△BDE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AE+EB=AB=6
cm.
22.(1)证明:∵AB=AC,
∴∠B=∠C.
在△DBE和△ECF中,
∴△DBE≌△ECF.
∴DE=EF.
∴△DEF是等腰三角形.
(2)解:由(1)可知△DBE≌△ECF,∴∠BDE=∠CEF.
∵∠A+∠B+∠C=180°,∠A=40°,
∠B=∠C,
∴∠B=×(180°-40°)=70°.
∴∠BDE+∠BED=110°.
∴∠CEF+∠BED=110°.
∴∠DEF=70°.
23.(1)证明:如图,过点D作DM⊥AB,DN⊥BF,垂足分别为M,N.
(第23题)
∵BD平分∠ABF,
∴DM=DN.
∵∠ADC=45°=∠ABC,
∴∠BAD=∠BCD.
又∵∠DMA=∠DNC=90°,
∴△ADM≌△CDN.
∴AD=CD.
(2)解:∵AD=CD,∠ADC=45°,
∴∠CAD=∠ACE=67.5°.
又∵∠CAB=45°,
∴∠AEC=67.5°.
∴∠ACE=∠AEC.
∴AE=AC=4.
24.解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,
∴BC=CA.
设BC=CA=x
cm,则OC=(45-x)cm,由勾股定理可知OB2+OC2=BC2,即152+(45-x)2=x2,解得x=25.
答:机器人行走的路程BC是25
cm.
25.解:根据题意,得AP=BQ=t
cm.
在△ABC中,AB=3
cm,∠B=60°,
∴BP=(3-t)cm.
若△PBQ是直角三角形,
则∠BQP=90°或∠BPQ=90°.
当∠BQP=90°时,BQ=BP,
即t=(3-t),
解得t=1;
当∠BPQ=90°时,BP=BQ,
即3-t=t,
解得t=2.
综上,当t=1或t=2时,△PBQ是直角三角形.
26.(1)证明:∵△BCD是等腰直角三角形,且∠BDC=90°,∴BD=CD,∠BDC=∠CDA=90°.
在△FBD和△ACD中,
∴△FBD≌△ACD(SAS).
(2)证明:∵BE⊥AC,
∴∠BEA=∠BEC=90°.
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE=BE,
∴△ABE≌△CBE(ASA),
∴AE=CE.∴CE=AC.
由(1)知△FBD≌△ACD,
∴BF=CA,∴CE=BF.
(3)解:BG2=GE2+CE2.证明如下:连接CG,∵H是BC边的中点,BD=CD,
∴HD垂直平分BC,∴BG=CG(线段垂直平分线上的点到这条线段两个端点的距离相等).∵BE⊥AC,
∴在Rt△CEG中,CG2=GE2+CE2,∴BG2=GE2+CE2.
点拨:本题综合考查全等三角形的判定与性质及通过添加辅助线利用勾股定理解决问题.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
