人教版数学八年级上册:11.2.1三角形的内角 课件(共40张PPT)
文档属性
| 名称 | 人教版数学八年级上册:11.2.1三角形的内角 课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 23:09:33 | ||
图片预览





文档简介
(共40张PPT)
11.2.1
三角形的内角和
学
习
目
标
1
1.掌握三角形内角和定理及其推论
2.会用添加辅助线的方法进行证明
3.灵活运用三角形内角和定理
重点
:
1、能用多种方法证明三角形内角和定理
2、会在证明中添加合适的辅助线。
3.证明三角形内角和的主要思想为:转化思想。
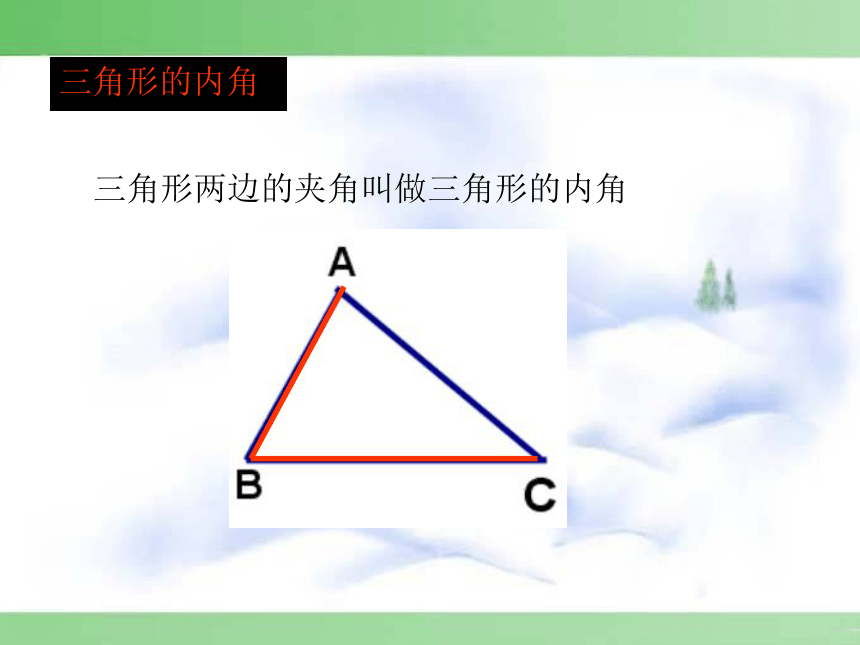
三角形两边的夹角叫做三角形的内角
三角形的内角
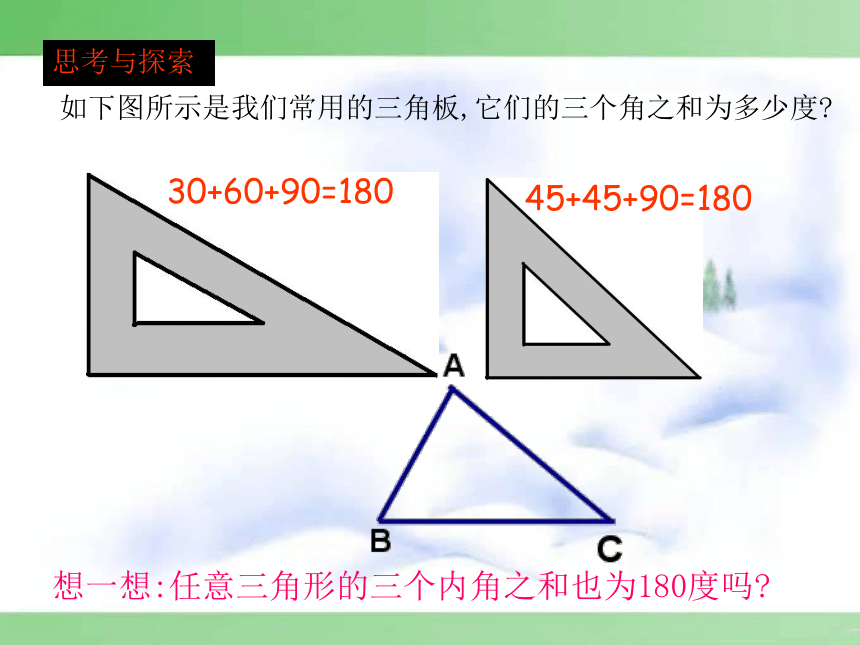
如下图所示是我们常用的三角板,它们的三个角之和为多少度?
想一想:任意三角形的三个内角之和也为180度吗?
30+60+90=180
45+45+90=180
思考与探索
把三个角拼在一起试试看
三角形的内角和是180度。
方法一:
A
B
C
1
2
3
方法二:
将各角沿着一边所在的直线折叠
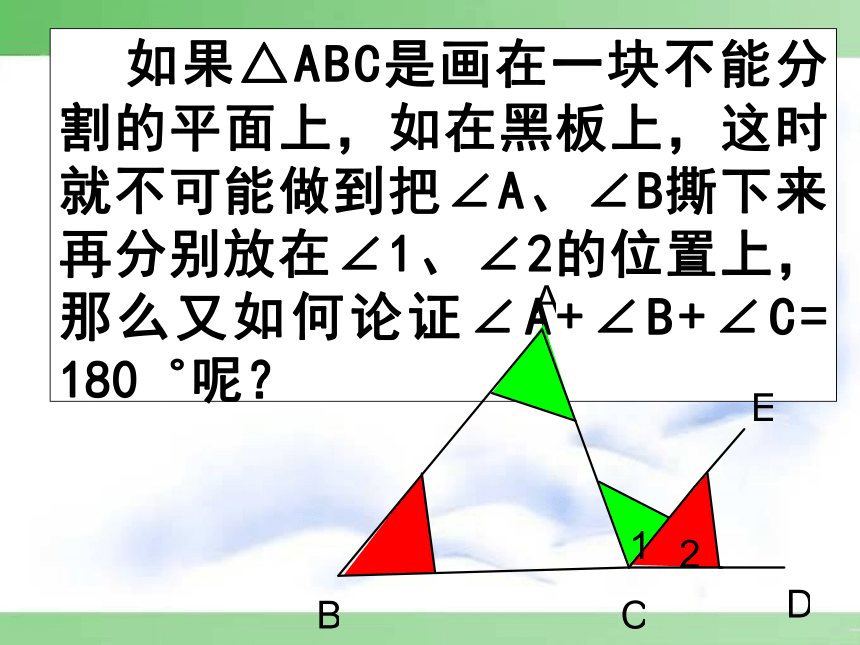
如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C=
180゜呢?
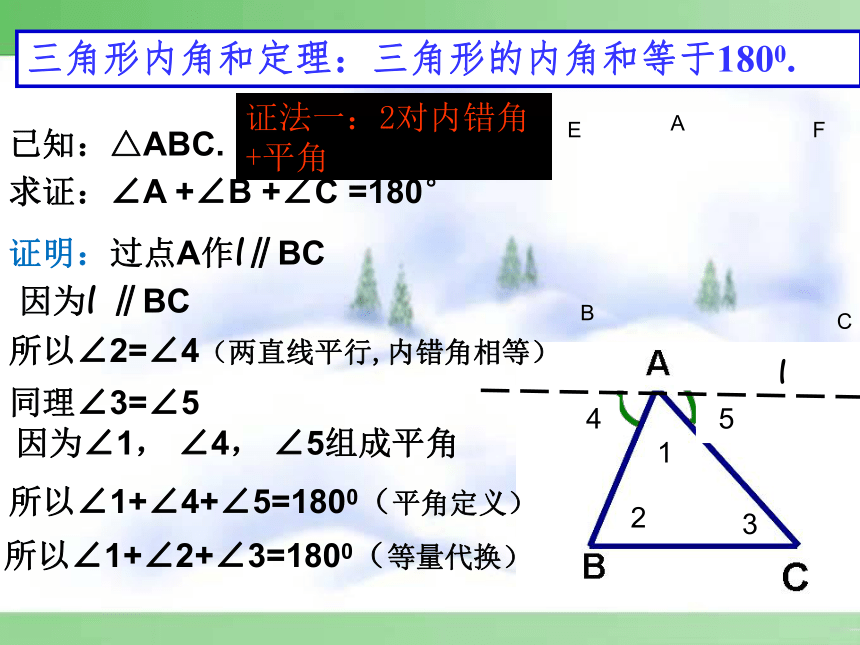
三角形内角和定理:三角形的内角和等于1800.
证明:过点A作l∥BC
所以∠2=∠4(两直线平行,内错角相等)
同理∠3=∠5
所以∠1+∠4+∠5=1800(平角定义)
所以∠1+∠2+∠3=1800(等量代换)
已知:△ABC.
A
B
C
E
F
求证:∠A
+∠B
+∠C
=180°
l
1
2
3
因为l
∥BC
因为∠1,
∠4,
∠5组成平角
5
4
证法一:2对内错角+平角
2
1
E
D
C
B
A
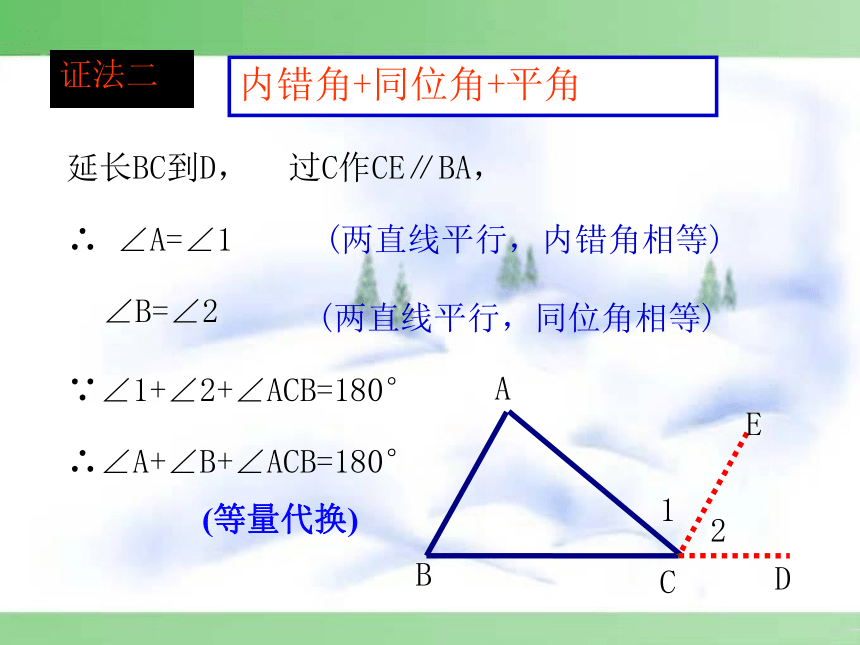
内错角+同位角+平角
延长BC到D,
过C作CE∥BA,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法二
(等量代换)
C
B
E
A
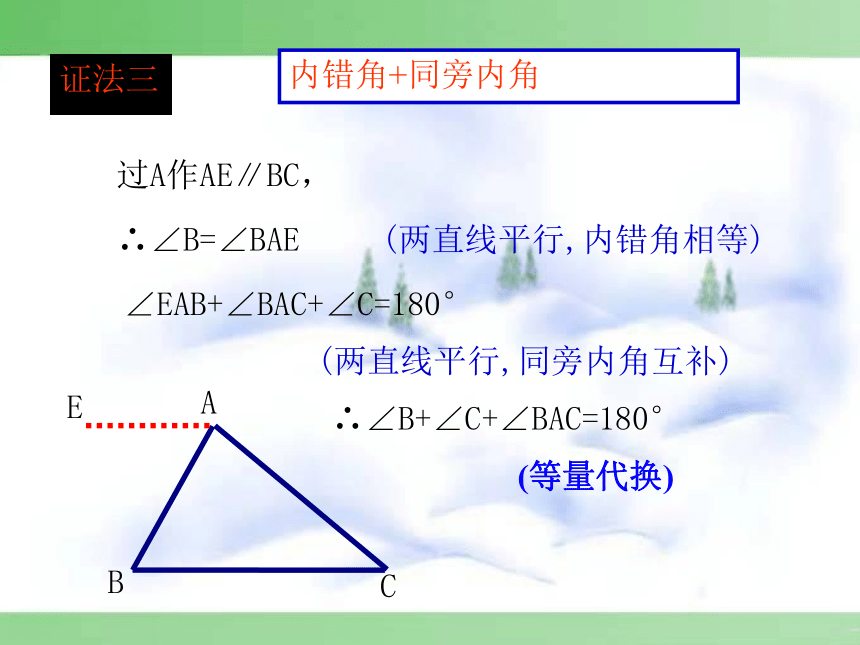
内错角+同旁内角
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
证法三
(等量代换)
E
D
C
B
A
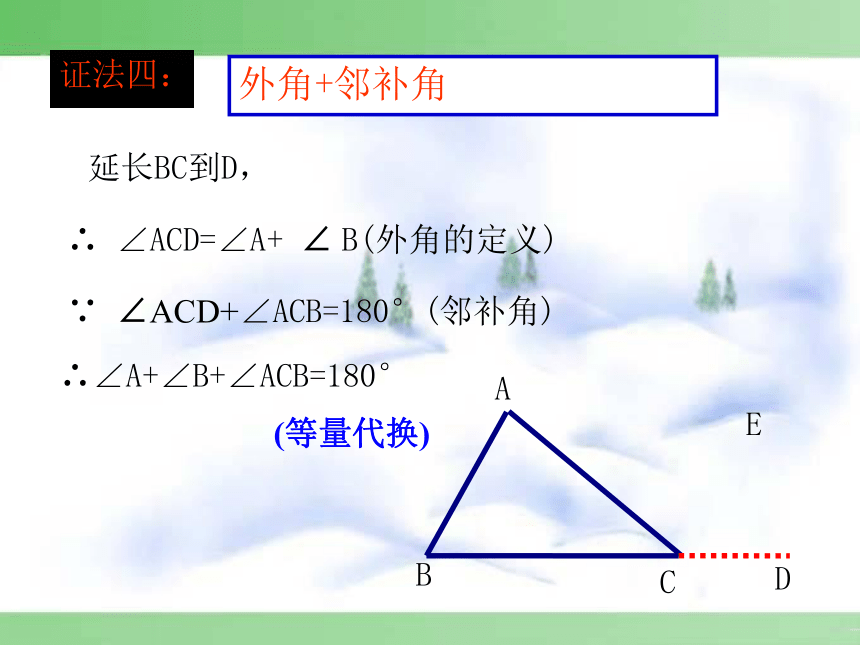
外角+邻补角
延长BC到D,
∴
∠ACD=∠A+
∠
B(外角的定义)
∵
∠ACD+∠ACB=180°(邻补角)
∴∠A+∠B+∠ACB=180°
证法四:
(等量代换)
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
思路总结
三角形内角和定理:
三角形的内角和等于1800.
即在△ABC中,
∠A
+∠B
+∠C=180
°
(口答)下列各组角是同一个三角形的内角吗?为什么?
(2)60°,
40°,
90°
(3)30°,
60°,
50°
(1)3°,
150°,
27°
(是
)
(
不是)
(
不是)
巩固练习
∠A+∠B+∠C=1800的几种变形:
∠A=1800
–(∠B+∠C).
∠B=1800
–(∠A+∠C).
∠C=1800
–(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
三种语言
?
A
B
C
C
B
A
2.推论:
直角三角形中,两锐角互余。
即在直角
△A
B
C
中,若∠C
=90°,
则∠A
+∠B
=90
°。
定理应用
三角形的三内角和是180?
,所以三内角可能出现的情况:
一个钝角
两个锐角
钝角三角形
锐角三角形
一个直角
两个锐角
直角三角形
三个都为锐角
钝角三角形
直角三角形
锐角三角形
例1:已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为20°,60°,100°。
思考:在△ABC中,如果∠A=
∠B=
∠
C,那么△ABC是什么三角形?
解:设∠A=x°,
那么∠B=2x°,∠C=3x°
根据题意得:
解得
∴∠A=30°,∠B=60°,∠C=90°
所以△ABC是直角三角形
如图:在△ABC中,∠BAC=40°,
∠B=75°,AD是△ABC的角平分线。求∠ADB的度数?
例2、
?
在△ABD中,
∠ADB=180°-∠B-∠BAD,
=
180
°-75
°-20
°=85
°
C
A
B
D
A
B
C
已知△ABC中,∠ABC=∠C=2∠A
,
BD是AC边上的高,求∠DBC的度数。
D
解:设∠A=x0,则∠ABC=∠C=2x0
∴x+2x+2x=180
(三角形内角和定理)
解得x=36
∴∠C=2×360=720
∴∠DBC=1800-900-720(三角形内角和定理)
在△BDC中,∵∠BDC=900
(三角形高的定义)
∴∠DBC=180
?
例题讲解3
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.
(1)∠DAC=_____
∠DAB=______
∠EBC=_______
∠CAB
=
______
A
(2)从C岛看A
、B两岛的视角∠C是多少?
50°
80°
40°
D
B
C
E
北
北
解:∵
AD∥BE
∴
∠DAB﹢∠ABE=180°
∴
∠ABE
=
180°-∠DAB
=
180°
-
80°
=100°
在△ABC中,∠C
=
180°
-
∠CAB
-
∠ABC
=
180°-30
°-60
°=90°
∴
∠ABC=∠ABE﹣∠CBE
30
°
=100°﹣40°=60°
例题讲解4
方法一
D
C
E
北
A
50°
∟
B
40
°
北
M
N
在△AMC中
∠AMC=90°,
∠MAC=50°
解:过点C画MN⊥AD分别交AD、BE于点M、N
1
2
方法二
∴∠1=180
°-90°-50°
=40°
∵
AD∥BE
∴
∠AMC+
∠BNC
=180
°
∴
∠BNC
=90°
同理得∠2
=50°
∴
∠ACB
=180
°
-∠1
-∠2
=180
°-40°-50°
=90°
B
D
C
E
北
A
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
解:
过点C画CF∥AD
∴
∠1=∠DAC=50
°,
F
∵
CF∥AD,
又AD
∥BE
∴
CF∥
BE
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1﹢∠2
=50
°﹢
40
°
=90
°
方法三
变式训练
如图,B处在A处的南偏西45
°方向,C处在A处的南偏东15
°方向,C处在B处的北偏东80
°方向,求∠ACB的度数。
思考1.
如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°,
求∠BDC的度数.
A
B
C
D
E
解:
∵∠A=70°
∴∠ACB=180
°-∠A-∠B
=180°-70°-50°
=60°
∵DE//BC
∴∠B=∠ADE=50°
∵
CD平分∠ACB
巩固练习
思考2:如图,直线AB∥CD,在AB、CD外有一点P,连结
PB、PD,交CD于E点。
则∠
B、
∠
D、
∠
P
之间是否存在一定的大小关系?给出证明。
A
B
C
P
D
E
(1)在△ABC中,∠A=35°,∠
B=43
°∠C=
.
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4则∠A
=
___
∠
B=
∠
C=
.
(3)
∠A
:
∠B
:∠C=3:2:1,问
△ABC是___三角形.
(4)
∠A
-∠C
=35
°∠B
-∠C
=10
°,则∠B
=?
(5)一个三角形中最多有
个直角,最多有___
个钝角,最多有__个锐角,至少有
个锐角。
(6)任意一个三角形中,最大的一个角的度数至少为
.(至少有一个角的度数小于或等于60)
应用新知
(7).△ABC中,若∠A+∠B=∠C,则△ABC是(
)
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
(8).
一个三角形至少有(
)
A、一个锐角
B、两个锐角
C、一个钝角
D、一个直角
B
B
巩固练习
(9)(2014聊城中考)在△ABC中,三个内角满足∠B-
∠A=
∠C-
∠B,求∠B的度数。
(10)(2014资阳中考)如图,AB⊥BD,AC
⊥CD,
∠A=35
°,求∠D的度数。
(11)如图,直线l1
//l2,
∠1=55。,
∠2=65。,求∠3的度数。
(12)如图,DE//FG,AC
⊥AB,
AC交FG于点C,∠1=60。,求∠2的度数。
(13)如图,将含有30。角的三角板放在两条平行线之间,已知∠1=20
。
,求∠2的度数。
(1)
(2)
(14)如图,在△ABC中,BE、CF是△ABC的高,交点为H,(1)∠ABC=66。,∠ACB=54。,求∠BHC的度数。
(2)探讨∠FHC与∠A的数量关系。
(15)如图,在△ABC中,AD是角平分线,∠ABC=66。,∠ACB=54。,DE
⊥AC于点E,求∠ADE的度数。
(16)如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB。(1)当∠A=60。,求∠BOC的度数。
(2)当∠A=x。,求∠BOC的度数。
17.如图,
BC
与AD相交于点E,探讨∠A+
∠B与∠C+
∠D的数量关系.
(18)如图,在△ABC中,
∠C
>
∠B,
AE平分∠
BAC交BC于E,过点A作△ABC的高AD,
(1)已知∠B=30
。
,
∠C=70
。
,求∠EAD的度数。
(2)探讨∠EAD与∠B、
∠C的数量关系。
(3)点F在射线AE
上,FD
⊥BC于点D,探究∠EFD与∠B、
∠C的数量关系。
小结
1、三角形的内角和定理:三角形内角和为180°
2、由三角形内角和等于180°,可得出
(1)推论:
直角三角形中,两锐角互余;
(2)一个三角形最多有一个直角、一个钝角、三个锐角,最少有两个锐角;
(3)一个三角形中至少有一个角小于或等于60°
3、三角形按角分类:
斜三角形
三角形
直角三角形
锐角三角形
钝角三角形
再见
11.2.1
三角形的内角和
学
习
目
标
1
1.掌握三角形内角和定理及其推论
2.会用添加辅助线的方法进行证明
3.灵活运用三角形内角和定理
重点
:
1、能用多种方法证明三角形内角和定理
2、会在证明中添加合适的辅助线。
3.证明三角形内角和的主要思想为:转化思想。
三角形两边的夹角叫做三角形的内角
三角形的内角
如下图所示是我们常用的三角板,它们的三个角之和为多少度?
想一想:任意三角形的三个内角之和也为180度吗?
30+60+90=180
45+45+90=180
思考与探索
把三个角拼在一起试试看
三角形的内角和是180度。
方法一:
A
B
C
1
2
3
方法二:
将各角沿着一边所在的直线折叠
如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C=
180゜呢?
三角形内角和定理:三角形的内角和等于1800.
证明:过点A作l∥BC
所以∠2=∠4(两直线平行,内错角相等)
同理∠3=∠5
所以∠1+∠4+∠5=1800(平角定义)
所以∠1+∠2+∠3=1800(等量代换)
已知:△ABC.
A
B
C
E
F
求证:∠A
+∠B
+∠C
=180°
l
1
2
3
因为l
∥BC
因为∠1,
∠4,
∠5组成平角
5
4
证法一:2对内错角+平角
2
1
E
D
C
B
A
内错角+同位角+平角
延长BC到D,
过C作CE∥BA,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法二
(等量代换)
C
B
E
A
内错角+同旁内角
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
证法三
(等量代换)
E
D
C
B
A
外角+邻补角
延长BC到D,
∴
∠ACD=∠A+
∠
B(外角的定义)
∵
∠ACD+∠ACB=180°(邻补角)
∴∠A+∠B+∠ACB=180°
证法四:
(等量代换)
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
思路总结
三角形内角和定理:
三角形的内角和等于1800.
即在△ABC中,
∠A
+∠B
+∠C=180
°
(口答)下列各组角是同一个三角形的内角吗?为什么?
(2)60°,
40°,
90°
(3)30°,
60°,
50°
(1)3°,
150°,
27°
(是
)
(
不是)
(
不是)
巩固练习
∠A+∠B+∠C=1800的几种变形:
∠A=1800
–(∠B+∠C).
∠B=1800
–(∠A+∠C).
∠C=1800
–(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
三种语言
?
A
B
C
C
B
A
2.推论:
直角三角形中,两锐角互余。
即在直角
△A
B
C
中,若∠C
=90°,
则∠A
+∠B
=90
°。
定理应用
三角形的三内角和是180?
,所以三内角可能出现的情况:
一个钝角
两个锐角
钝角三角形
锐角三角形
一个直角
两个锐角
直角三角形
三个都为锐角
钝角三角形
直角三角形
锐角三角形
例1:已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为20°,60°,100°。
思考:在△ABC中,如果∠A=
∠B=
∠
C,那么△ABC是什么三角形?
解:设∠A=x°,
那么∠B=2x°,∠C=3x°
根据题意得:
解得
∴∠A=30°,∠B=60°,∠C=90°
所以△ABC是直角三角形
如图:在△ABC中,∠BAC=40°,
∠B=75°,AD是△ABC的角平分线。求∠ADB的度数?
例2、
?
在△ABD中,
∠ADB=180°-∠B-∠BAD,
=
180
°-75
°-20
°=85
°
C
A
B
D
A
B
C
已知△ABC中,∠ABC=∠C=2∠A
,
BD是AC边上的高,求∠DBC的度数。
D
解:设∠A=x0,则∠ABC=∠C=2x0
∴x+2x+2x=180
(三角形内角和定理)
解得x=36
∴∠C=2×360=720
∴∠DBC=1800-900-720(三角形内角和定理)
在△BDC中,∵∠BDC=900
(三角形高的定义)
∴∠DBC=180
?
例题讲解3
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.
(1)∠DAC=_____
∠DAB=______
∠EBC=_______
∠CAB
=
______
A
(2)从C岛看A
、B两岛的视角∠C是多少?
50°
80°
40°
D
B
C
E
北
北
解:∵
AD∥BE
∴
∠DAB﹢∠ABE=180°
∴
∠ABE
=
180°-∠DAB
=
180°
-
80°
=100°
在△ABC中,∠C
=
180°
-
∠CAB
-
∠ABC
=
180°-30
°-60
°=90°
∴
∠ABC=∠ABE﹣∠CBE
30
°
=100°﹣40°=60°
例题讲解4
方法一
D
C
E
北
A
50°
∟
B
40
°
北
M
N
在△AMC中
∠AMC=90°,
∠MAC=50°
解:过点C画MN⊥AD分别交AD、BE于点M、N
1
2
方法二
∴∠1=180
°-90°-50°
=40°
∵
AD∥BE
∴
∠AMC+
∠BNC
=180
°
∴
∠BNC
=90°
同理得∠2
=50°
∴
∠ACB
=180
°
-∠1
-∠2
=180
°-40°-50°
=90°
B
D
C
E
北
A
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
解:
过点C画CF∥AD
∴
∠1=∠DAC=50
°,
F
∵
CF∥AD,
又AD
∥BE
∴
CF∥
BE
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1﹢∠2
=50
°﹢
40
°
=90
°
方法三
变式训练
如图,B处在A处的南偏西45
°方向,C处在A处的南偏东15
°方向,C处在B处的北偏东80
°方向,求∠ACB的度数。
思考1.
如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°,
求∠BDC的度数.
A
B
C
D
E
解:
∵∠A=70°
∴∠ACB=180
°-∠A-∠B
=180°-70°-50°
=60°
∵DE//BC
∴∠B=∠ADE=50°
∵
CD平分∠ACB
巩固练习
思考2:如图,直线AB∥CD,在AB、CD外有一点P,连结
PB、PD,交CD于E点。
则∠
B、
∠
D、
∠
P
之间是否存在一定的大小关系?给出证明。
A
B
C
P
D
E
(1)在△ABC中,∠A=35°,∠
B=43
°∠C=
.
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4则∠A
=
___
∠
B=
∠
C=
.
(3)
∠A
:
∠B
:∠C=3:2:1,问
△ABC是___三角形.
(4)
∠A
-∠C
=35
°∠B
-∠C
=10
°,则∠B
=?
(5)一个三角形中最多有
个直角,最多有___
个钝角,最多有__个锐角,至少有
个锐角。
(6)任意一个三角形中,最大的一个角的度数至少为
.(至少有一个角的度数小于或等于60)
应用新知
(7).△ABC中,若∠A+∠B=∠C,则△ABC是(
)
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
(8).
一个三角形至少有(
)
A、一个锐角
B、两个锐角
C、一个钝角
D、一个直角
B
B
巩固练习
(9)(2014聊城中考)在△ABC中,三个内角满足∠B-
∠A=
∠C-
∠B,求∠B的度数。
(10)(2014资阳中考)如图,AB⊥BD,AC
⊥CD,
∠A=35
°,求∠D的度数。
(11)如图,直线l1
//l2,
∠1=55。,
∠2=65。,求∠3的度数。
(12)如图,DE//FG,AC
⊥AB,
AC交FG于点C,∠1=60。,求∠2的度数。
(13)如图,将含有30。角的三角板放在两条平行线之间,已知∠1=20
。
,求∠2的度数。
(1)
(2)
(14)如图,在△ABC中,BE、CF是△ABC的高,交点为H,(1)∠ABC=66。,∠ACB=54。,求∠BHC的度数。
(2)探讨∠FHC与∠A的数量关系。
(15)如图,在△ABC中,AD是角平分线,∠ABC=66。,∠ACB=54。,DE
⊥AC于点E,求∠ADE的度数。
(16)如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB。(1)当∠A=60。,求∠BOC的度数。
(2)当∠A=x。,求∠BOC的度数。
17.如图,
BC
与AD相交于点E,探讨∠A+
∠B与∠C+
∠D的数量关系.
(18)如图,在△ABC中,
∠C
>
∠B,
AE平分∠
BAC交BC于E,过点A作△ABC的高AD,
(1)已知∠B=30
。
,
∠C=70
。
,求∠EAD的度数。
(2)探讨∠EAD与∠B、
∠C的数量关系。
(3)点F在射线AE
上,FD
⊥BC于点D,探究∠EFD与∠B、
∠C的数量关系。
小结
1、三角形的内角和定理:三角形内角和为180°
2、由三角形内角和等于180°,可得出
(1)推论:
直角三角形中,两锐角互余;
(2)一个三角形最多有一个直角、一个钝角、三个锐角,最少有两个锐角;
(3)一个三角形中至少有一个角小于或等于60°
3、三角形按角分类:
斜三角形
三角形
直角三角形
锐角三角形
钝角三角形
再见
