人教版八年级上册 11.2.2三角形的外角 课件(共42张PPT)
文档属性
| 名称 | 人教版八年级上册 11.2.2三角形的外角 课件(共42张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 14:23:34 | ||
图片预览








文档简介
(共42张PPT)
11.2.2
三角形外角
11.2.2三角形的外角
希望同学们像雄鹰在蓝天翱翔
学习目标:
1.理解三角形的外角的概念.
2.掌握三角形的一个外角等于与它不相邻的两个内角的和.
学习重点:
掌握三角形的一个外角等于与它不相邻的两个内角的和.
一、
打好基础
(1)什么是三角形的内角?
(2)三角形的内角和是多少?
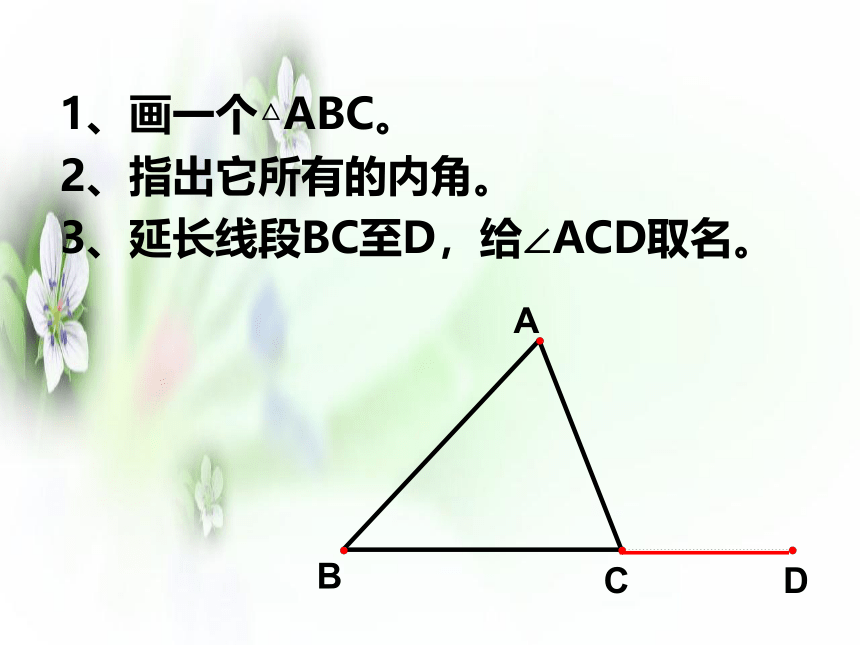
1、画一个△ABC。
2、指出它所有的内角。
3、延长线段BC至D,给∠ACD取名。
1、外角的概念:三角形的一边与另一边的延长线所组成的角叫做三角形的外角。
思考:
1、△ABC有多少个外角?
2、作出△ABC的所有外角,并说出来。
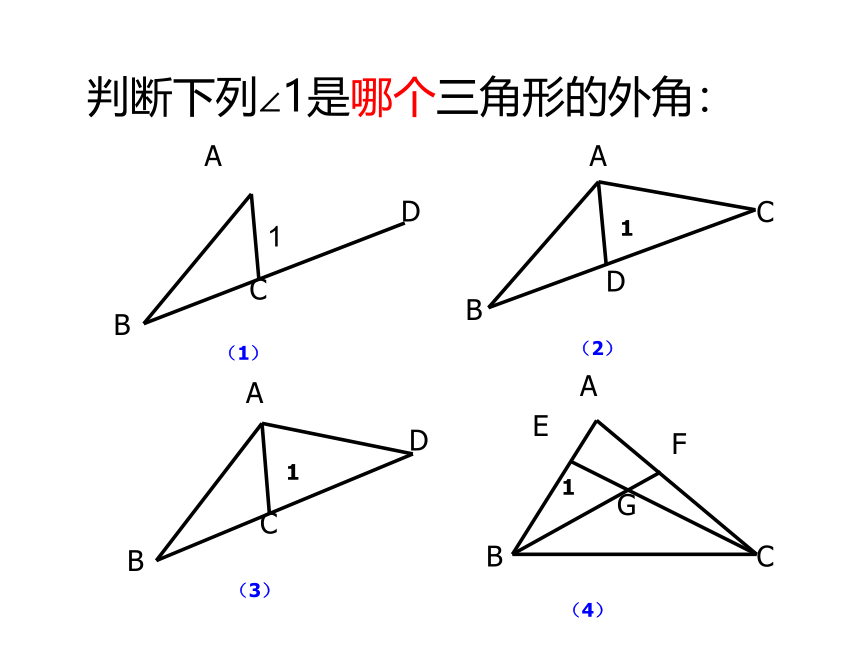
判断下列∠1是哪个三角形的外角:
A
B
C
E
F
G
1
(4)
A
B
C
D
1
(2)
A
B
C
D
1
(3)
A
B
C
D
(1)
1
二、新知探索
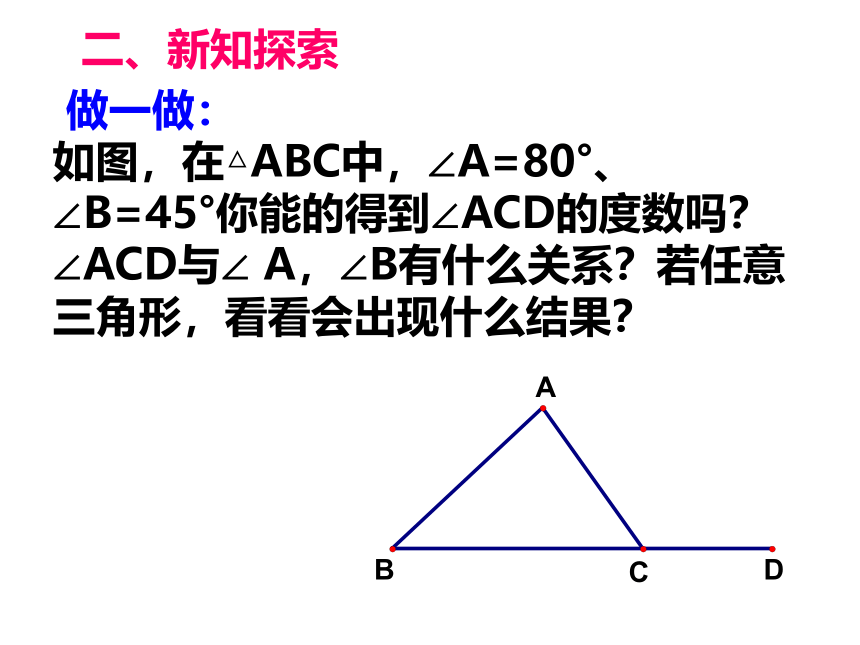
做一做:
如图,在△ABC中,∠A=80°、
∠B=45°你能的得到∠ACD的度数吗?
∠ACD与∠
A,∠B有什么关系?若任意三角形,看看会出现什么结果?
探索:
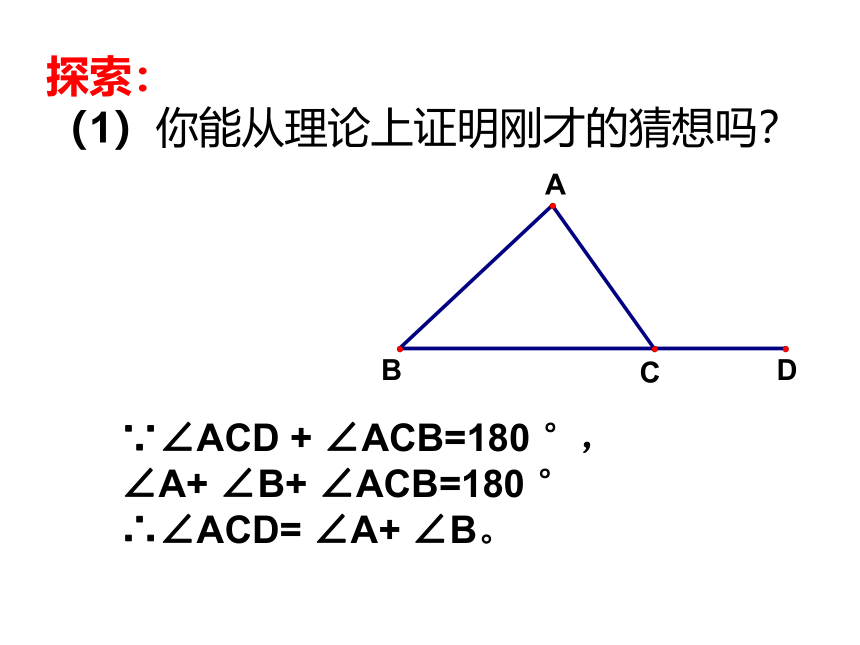
(1)你能从理论上证明刚才的猜想吗?
∵∠ACD
+
∠ACB=180
°,
∠A+
∠B+
∠ACB=180
°
∴∠ACD=
∠A+
∠B。
(2)如图:
过点C作C
E∥A
B
。
∴∠1=∠
B,∠2=∠A。
∴∠A
CD=∠1+∠2=∠B+∠A。
E
1
2
思考:你能过A点或C点作它们对边的平行线,来说明∠CBD=∠ACB+∠CAB吗?
试一下吧!
C
A
B
D
(4)
C
A
B
D
(3)
E
E
三角形外角性质的其它解法
如图:D是△ABC边BC上一点,
∴∠ADC=
+
。
∴∠ADC>
,
∠ADC>
。
问:
∠
ADB=
_____+
_____。
∠DAC
∠C
∠DAB
∠B
∠DAB
∠B
练习1:求下列各图中∠1的度数。
把图中∠1、
∠2、
∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
三、归纳:
三角形外角的性质:
(1)三角形的一个外角等于和它不相邻的两个内角的和;
(2)三角形的一个外角大于任何一个和它不相邻的内角。
例1.已知,如图,AE∥CD,
∠C=80°,∠A=45°,
求∠B的度数。
B
A
F
C
D
E
例2:已知D是△ABC的BC边上一 点,∠B=∠BAD,
∠ADC=80°
,
∠BAC=70
°
,求∠B,
∠C的度数。
活学活用
1.(新疆中考)将一副三角板按图中方式叠放,
(1)则∠a=______.
(2)∠
1=________,
∠2=______.
(3)
∠3=________.
注意:我们讲三角形的外角和时,在三角形的每一个顶点处只取一个外角。
我们知道三角形的内角和是180°,那么三角形的外角和是多少?
例3.如图,已知∠1,∠2,∠3是△ABC的外角,求证:
∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:∵∠1,∠2,∠3是△ABC的外角,
∴
∠1=
∠4+
∠5,∠2=
∠4+
∠6
∠3=
∠5+
∠6
∴∠1+∠2+∠3
=∠4+
∠5+∠4+
∠6+∠5+
∠6
=2(∠4+
∠5
+∠6)
=360°
A
B
C
1
2
3
(3)三角形三个外角和是360°
练习2:在△
ABC中,
∠A+
∠B=100°,
∠C=4∠A,
求∠A,∠B及与∠C相邻的外角。
练习3、△ABC中,点D在BC上,点F
在BA的延长线上,DF交AC于点E,
∠B=42°
,∠C=55°
,∠DEC=45,
求∠F
1.已知图中∠A、∠B、∠C分别为80°,
20°,30°,求∠1的度数
B
3
2
1
A
C
D
E
当堂检测
2.如图,AD是∠CAE的平分线,
∠B=35
°,
∠DAE=60
°,求∠ACD的度数。
3.如图,已知AD
∥BC,
∠B=30
°,DB平分∠ADE,求∠DEC的度数。
4.如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
5.如图,在△
ABC中,
∠B=
∠C,AE平分△ABC的外角∠
DAC,问AE与BC平行吗?为什么?
6.如图,试计算∠BOC的度数.
90?
30?
20?
A
B
C
O
D
⌒
110°
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
360°
1
2
3
N
P
M
3
P
7.
A
B
C
D
E
8.(1)求∠A+
∠B+
∠C+
∠D+
∠E的度数
⌒
F
G
⌒
∠EGD
+
∠EFA
+
∠E
=
180°
解:∵∠A+
∠C=
∠EFA
∴
∠A+
∠B+
∠C+
∠D+
∠E=
180°
∠B+
∠D=
∠EGD
(2)变形后,请求出∠A+
∠B+
∠C+
∠D+
∠E的度数。
9.如图,在△ABC中,AB>AC,
∠AEF=
∠
AFE,延长EF与BC的延长线交于点G。
求证:
2∠G=
∠ACB—∠B。
10.如图,在△ABC中,角平分线AD、BE、CF相交于点H,过点A作AG⊥BE于点G,
(1)若∠ABC=60
°
,∠BAC=40
°
,求∠HAG的度数。
(2)2∠HAG=
∠ACB吗?为什么?
4
11.如图,在△ABC中,角平分线AD、BE、CF相交于点P,过点P作PG
⊥BC于点G,猜测∠BPD与∠
CPG的数量关系,并说明理由。
12.如图,在△ABC中,AD平分∠BAC,点P在AD上,PE⊥AD交直线BC于点E.
(1)若∠B=35
°,
∠ACB=85
°,求∠E的度数.
(2)当点P在线段AD上运动时,猜想∠E
与∠B、
∠ACB的数量关系。
13.如图,OD
⊥
OE,点A、点B分别是OD、OE上的动点,
∠ABO的平分线与
∠DAB的平分线的反向延长线交于点F,猜测∠F的度数,并证明。
14.如图,在△ABC中,
∠ABC的平分线与外角∠ACD的平分线交于点P。
(1)若∠ABC=40
°
,
∠ACB=80
°,求∠P的度数;
(2)若∠A=60
°
,求∠P的度数。
(3)
∠A与∠P之间有怎样的数量关系?说明理由。
(4)若∠A=x°,
∠ABC与∠ACD的平分线交于点P1,
∠
P1
BC与∠
P1
CD的平分线交于点P2,依次下去,求∠P2014的度数。
15.(1)如图1.若点P是∠ABC和∠ACB的平分线的交点,试说明∠P=90
°
+
∠A
;
(2)如图2,若点P是∠ABC和外角∠ACD的角平分线的交点,试说明∠P=
∠A
;
16.如图,△ABC的外角∠
DBC与外角∠ECB
的平分线相交于点P,
(1)若∠ABC=30
°
,
∠ACB=70
°
,求∠BPC的度数。
(2)若∠A=60
°
,求∠BPC的度数。
(3)探讨∠BPC与∠A的数量关系。
小结
1、三角形外角的两条性质
①
三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360°。
11.2.2
三角形外角
11.2.2三角形的外角
希望同学们像雄鹰在蓝天翱翔
学习目标:
1.理解三角形的外角的概念.
2.掌握三角形的一个外角等于与它不相邻的两个内角的和.
学习重点:
掌握三角形的一个外角等于与它不相邻的两个内角的和.
一、
打好基础
(1)什么是三角形的内角?
(2)三角形的内角和是多少?
1、画一个△ABC。
2、指出它所有的内角。
3、延长线段BC至D,给∠ACD取名。
1、外角的概念:三角形的一边与另一边的延长线所组成的角叫做三角形的外角。
思考:
1、△ABC有多少个外角?
2、作出△ABC的所有外角,并说出来。
判断下列∠1是哪个三角形的外角:
A
B
C
E
F
G
1
(4)
A
B
C
D
1
(2)
A
B
C
D
1
(3)
A
B
C
D
(1)
1
二、新知探索
做一做:
如图,在△ABC中,∠A=80°、
∠B=45°你能的得到∠ACD的度数吗?
∠ACD与∠
A,∠B有什么关系?若任意三角形,看看会出现什么结果?
探索:
(1)你能从理论上证明刚才的猜想吗?
∵∠ACD
+
∠ACB=180
°,
∠A+
∠B+
∠ACB=180
°
∴∠ACD=
∠A+
∠B。
(2)如图:
过点C作C
E∥A
B
。
∴∠1=∠
B,∠2=∠A。
∴∠A
CD=∠1+∠2=∠B+∠A。
E
1
2
思考:你能过A点或C点作它们对边的平行线,来说明∠CBD=∠ACB+∠CAB吗?
试一下吧!
C
A
B
D
(4)
C
A
B
D
(3)
E
E
三角形外角性质的其它解法
如图:D是△ABC边BC上一点,
∴∠ADC=
+
。
∴∠ADC>
,
∠ADC>
。
问:
∠
ADB=
_____+
_____。
∠DAC
∠C
∠DAB
∠B
∠DAB
∠B
练习1:求下列各图中∠1的度数。
把图中∠1、
∠2、
∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
三、归纳:
三角形外角的性质:
(1)三角形的一个外角等于和它不相邻的两个内角的和;
(2)三角形的一个外角大于任何一个和它不相邻的内角。
例1.已知,如图,AE∥CD,
∠C=80°,∠A=45°,
求∠B的度数。
B
A
F
C
D
E
例2:已知D是△ABC的BC边上一 点,∠B=∠BAD,
∠ADC=80°
,
∠BAC=70
°
,求∠B,
∠C的度数。
活学活用
1.(新疆中考)将一副三角板按图中方式叠放,
(1)则∠a=______.
(2)∠
1=________,
∠2=______.
(3)
∠3=________.
注意:我们讲三角形的外角和时,在三角形的每一个顶点处只取一个外角。
我们知道三角形的内角和是180°,那么三角形的外角和是多少?
例3.如图,已知∠1,∠2,∠3是△ABC的外角,求证:
∠1+∠2+∠3=360°
A
B
C
1
2
3
证明:∵∠1,∠2,∠3是△ABC的外角,
∴
∠1=
∠4+
∠5,∠2=
∠4+
∠6
∠3=
∠5+
∠6
∴∠1+∠2+∠3
=∠4+
∠5+∠4+
∠6+∠5+
∠6
=2(∠4+
∠5
+∠6)
=360°
A
B
C
1
2
3
(3)三角形三个外角和是360°
练习2:在△
ABC中,
∠A+
∠B=100°,
∠C=4∠A,
求∠A,∠B及与∠C相邻的外角。
练习3、△ABC中,点D在BC上,点F
在BA的延长线上,DF交AC于点E,
∠B=42°
,∠C=55°
,∠DEC=45,
求∠F
1.已知图中∠A、∠B、∠C分别为80°,
20°,30°,求∠1的度数
B
3
2
1
A
C
D
E
当堂检测
2.如图,AD是∠CAE的平分线,
∠B=35
°,
∠DAE=60
°,求∠ACD的度数。
3.如图,已知AD
∥BC,
∠B=30
°,DB平分∠ADE,求∠DEC的度数。
4.如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
5.如图,在△
ABC中,
∠B=
∠C,AE平分△ABC的外角∠
DAC,问AE与BC平行吗?为什么?
6.如图,试计算∠BOC的度数.
90?
30?
20?
A
B
C
O
D
⌒
110°
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
360°
1
2
3
N
P
M
3
P
7.
A
B
C
D
E
8.(1)求∠A+
∠B+
∠C+
∠D+
∠E的度数
⌒
F
G
⌒
∠EGD
+
∠EFA
+
∠E
=
180°
解:∵∠A+
∠C=
∠EFA
∴
∠A+
∠B+
∠C+
∠D+
∠E=
180°
∠B+
∠D=
∠EGD
(2)变形后,请求出∠A+
∠B+
∠C+
∠D+
∠E的度数。
9.如图,在△ABC中,AB>AC,
∠AEF=
∠
AFE,延长EF与BC的延长线交于点G。
求证:
2∠G=
∠ACB—∠B。
10.如图,在△ABC中,角平分线AD、BE、CF相交于点H,过点A作AG⊥BE于点G,
(1)若∠ABC=60
°
,∠BAC=40
°
,求∠HAG的度数。
(2)2∠HAG=
∠ACB吗?为什么?
4
11.如图,在△ABC中,角平分线AD、BE、CF相交于点P,过点P作PG
⊥BC于点G,猜测∠BPD与∠
CPG的数量关系,并说明理由。
12.如图,在△ABC中,AD平分∠BAC,点P在AD上,PE⊥AD交直线BC于点E.
(1)若∠B=35
°,
∠ACB=85
°,求∠E的度数.
(2)当点P在线段AD上运动时,猜想∠E
与∠B、
∠ACB的数量关系。
13.如图,OD
⊥
OE,点A、点B分别是OD、OE上的动点,
∠ABO的平分线与
∠DAB的平分线的反向延长线交于点F,猜测∠F的度数,并证明。
14.如图,在△ABC中,
∠ABC的平分线与外角∠ACD的平分线交于点P。
(1)若∠ABC=40
°
,
∠ACB=80
°,求∠P的度数;
(2)若∠A=60
°
,求∠P的度数。
(3)
∠A与∠P之间有怎样的数量关系?说明理由。
(4)若∠A=x°,
∠ABC与∠ACD的平分线交于点P1,
∠
P1
BC与∠
P1
CD的平分线交于点P2,依次下去,求∠P2014的度数。
15.(1)如图1.若点P是∠ABC和∠ACB的平分线的交点,试说明∠P=90
°
+
∠A
;
(2)如图2,若点P是∠ABC和外角∠ACD的角平分线的交点,试说明∠P=
∠A
;
16.如图,△ABC的外角∠
DBC与外角∠ECB
的平分线相交于点P,
(1)若∠ABC=30
°
,
∠ACB=70
°
,求∠BPC的度数。
(2)若∠A=60
°
,求∠BPC的度数。
(3)探讨∠BPC与∠A的数量关系。
小结
1、三角形外角的两条性质
①
三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360°。
