人教版八年级上册 数学 课件 12.1全等三角形(共22张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 课件 12.1全等三角形(共22张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
全等三角形
人教版八年级上册第12章
下列各组图形的形状与大小有什么特点?
观察
下列各组图形的形状与大小有什么特点?
思考:他们能完全重合吗?
观察
把一块三角板按在纸上,画下图形,照图形剪下纸板。剪下的纸板与三角板大小、形状完全相同吗?他们能够完全重合吗?
想一想
形状、大小相同的图形放在一起能够完全重合
能够完全重合的两个图形叫做全等形
定义
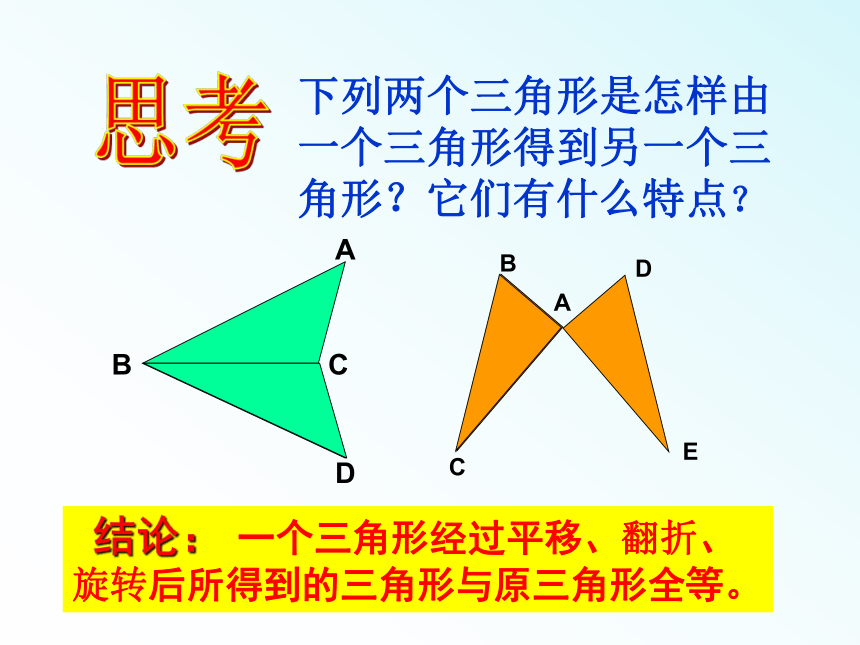
下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
B
A
C
N
P
M
A
C
B
D
E
下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
A
B
C
D
C
B
A
D
E
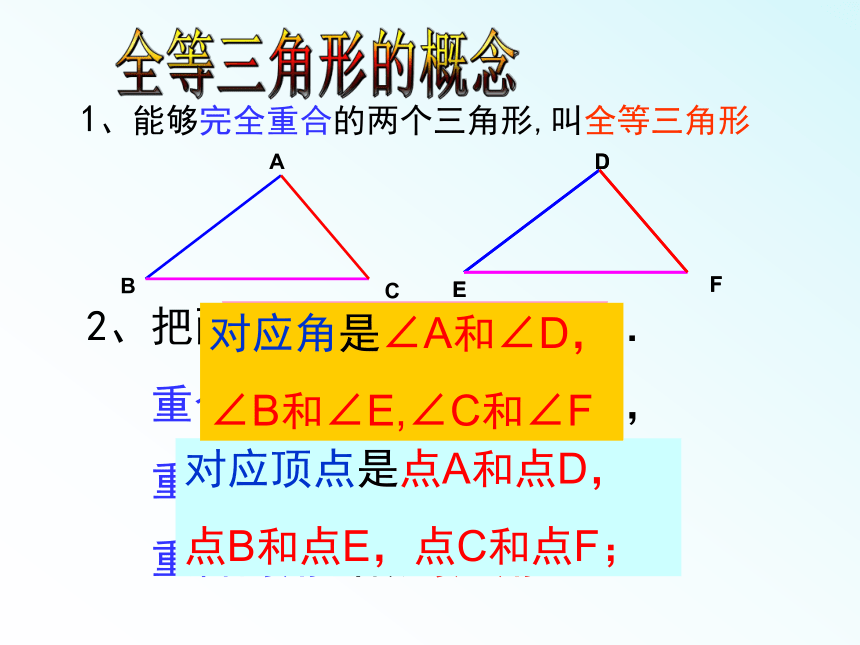
结论:
一个三角形经过平移、翻折、旋转后所得到的三角形与原三角形全等。
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫全等三角形
E
D
F
2、把两个三角形重合到一起.
重合的顶点叫做对应顶点,
重合的边叫做对应边,
重合的角叫做对应角。
全等三角形的概念
对应顶点是点A和点D,
点B和点E,点C和点F;
对应边是AB和DE,
AC和DF,BC和EF;
对应角是∠A和∠D,
∠B和∠E,∠C和∠F
A
B
C
E
D
F
“全等”用符号“≌
”表示
图中的△ABC和△DEF全等,
记作:△ABC≌
△DEF
读作:△ABC全等于△DEF
全等三角形的表示
你能否直接从记作?ABC≌
?DEF中判断出所有的对应顶点、对应边和对应角?
A
B
C
D
E
F
≌
?
≌
√
注意
记作两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
寻找各图中两个全等三角形的对应元素。
观察与思考
E
A
D
C
B
F
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌
△DFE
∴
AB=DF,
BC=FE,
AC=DE
符号语言:
∵△ABC≌
△DFE
∴∠A=∠D,∠B=∠F,∠C=∠E
D
E
F
A
B
C
全等三角形的性质
例题讲解,掌握新知
例1:如图,
△ABC≌△DCB,
指出所有的对应边和对应角。
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,
AC与BD是对应边
∠A与∠
D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角
例题讲解,掌握新知
O
D
C
B
A
例2:图中△ABO≌△DCO,试写出这两个三角形中相等的边和相等的角。
解:∵△ABO≌△DCO
∴
AB=DC,BO=CO,AO=DO
∠A=∠
D,∠ABO=∠DCO,∠AOB=∠DOC
A
B
C
D
E
F
∵△ACB≌△DEF
∴AB=DF,
CB=EF,AC=DE.
∴∠A=∠D,∠CBA=∠F,∠C=
∠DEF.
先写出全等式,再指出它们的对应边和对应角
探究交流
A
B
C
D
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD
∠C=
∠D.
规律:有公共边的,公共边是对应边
先写出全等式,再指出它们的对应边和对应角
探究交流
A
C
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC=
∠BOD.
规律:有对顶角的,对顶角是对应角
o
先写出全等式,再指出它们的对应边和对应角
探究交流
A
B
C
D
E
∵△ABC≌△ADE
∴AB=AD,AC=AE,
BC=DE
∴∠A=∠A,∠B=∠D,
∠ACB=
∠AED.
规律:有公共角的,公共角是对应角
先写出全等式,再指出它们的对应边和对应角
探究交流
先写出全等式,再指出它们的对应边和对应角
解∵△ABC≌△FDE
∴
AB=FD,AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB=
∠FED.
一对最大的角是对应角
一对最小的角是对应角
A
B
C
F
D
E
规律:
一对最长的边是对应边
一对最短的边是对应边
探究交流
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,对应边所对的角是对应角.
5.在两个全等三角形中最长边对应最长边,最短边对应最短边,最大角对应最大角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
找对应边对应角的规律
互相重合的角叫做___
互相重合的边叫做____
其中:互相重合的顶点叫做___
2.
叫全等三角形。
1.能够重合的两个图形叫做
。
全等形
4.全等三角形的
和
相等
对应边
对应角
对应顶点
课
堂
小
结
能够完全重合的两个三角形
3.“全等”用符号“
”来表示,读作“
”
对应边
对应角
5.书写全等式时要求把
对应字母写在对应的位置上
全等于
≌
作业:小练习册
谢谢大家,欢迎指导
全等三角形
人教版八年级上册第12章
下列各组图形的形状与大小有什么特点?
观察
下列各组图形的形状与大小有什么特点?
思考:他们能完全重合吗?
观察
把一块三角板按在纸上,画下图形,照图形剪下纸板。剪下的纸板与三角板大小、形状完全相同吗?他们能够完全重合吗?
想一想
形状、大小相同的图形放在一起能够完全重合
能够完全重合的两个图形叫做全等形
定义
下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
B
A
C
N
P
M
A
C
B
D
E
下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
A
B
C
D
C
B
A
D
E
结论:
一个三角形经过平移、翻折、旋转后所得到的三角形与原三角形全等。
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫全等三角形
E
D
F
2、把两个三角形重合到一起.
重合的顶点叫做对应顶点,
重合的边叫做对应边,
重合的角叫做对应角。
全等三角形的概念
对应顶点是点A和点D,
点B和点E,点C和点F;
对应边是AB和DE,
AC和DF,BC和EF;
对应角是∠A和∠D,
∠B和∠E,∠C和∠F
A
B
C
E
D
F
“全等”用符号“≌
”表示
图中的△ABC和△DEF全等,
记作:△ABC≌
△DEF
读作:△ABC全等于△DEF
全等三角形的表示
你能否直接从记作?ABC≌
?DEF中判断出所有的对应顶点、对应边和对应角?
A
B
C
D
E
F
≌
?
≌
√
注意
记作两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
寻找各图中两个全等三角形的对应元素。
观察与思考
E
A
D
C
B
F
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌
△DFE
∴
AB=DF,
BC=FE,
AC=DE
符号语言:
∵△ABC≌
△DFE
∴∠A=∠D,∠B=∠F,∠C=∠E
D
E
F
A
B
C
全等三角形的性质
例题讲解,掌握新知
例1:如图,
△ABC≌△DCB,
指出所有的对应边和对应角。
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,
AC与BD是对应边
∠A与∠
D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角
例题讲解,掌握新知
O
D
C
B
A
例2:图中△ABO≌△DCO,试写出这两个三角形中相等的边和相等的角。
解:∵△ABO≌△DCO
∴
AB=DC,BO=CO,AO=DO
∠A=∠
D,∠ABO=∠DCO,∠AOB=∠DOC
A
B
C
D
E
F
∵△ACB≌△DEF
∴AB=DF,
CB=EF,AC=DE.
∴∠A=∠D,∠CBA=∠F,∠C=
∠DEF.
先写出全等式,再指出它们的对应边和对应角
探究交流
A
B
C
D
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD
∠C=
∠D.
规律:有公共边的,公共边是对应边
先写出全等式,再指出它们的对应边和对应角
探究交流
A
C
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC=
∠BOD.
规律:有对顶角的,对顶角是对应角
o
先写出全等式,再指出它们的对应边和对应角
探究交流
A
B
C
D
E
∵△ABC≌△ADE
∴AB=AD,AC=AE,
BC=DE
∴∠A=∠A,∠B=∠D,
∠ACB=
∠AED.
规律:有公共角的,公共角是对应角
先写出全等式,再指出它们的对应边和对应角
探究交流
先写出全等式,再指出它们的对应边和对应角
解∵△ABC≌△FDE
∴
AB=FD,AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB=
∠FED.
一对最大的角是对应角
一对最小的角是对应角
A
B
C
F
D
E
规律:
一对最长的边是对应边
一对最短的边是对应边
探究交流
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,对应边所对的角是对应角.
5.在两个全等三角形中最长边对应最长边,最短边对应最短边,最大角对应最大角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
找对应边对应角的规律
互相重合的角叫做___
互相重合的边叫做____
其中:互相重合的顶点叫做___
2.
叫全等三角形。
1.能够重合的两个图形叫做
。
全等形
4.全等三角形的
和
相等
对应边
对应角
对应顶点
课
堂
小
结
能够完全重合的两个三角形
3.“全等”用符号“
”来表示,读作“
”
对应边
对应角
5.书写全等式时要求把
对应字母写在对应的位置上
全等于
≌
作业:小练习册
谢谢大家,欢迎指导
