人教版数学九年级上册24.2.2 直线和圆的位置关系教学课件(第1课时 17张)
文档属性
| 名称 | 人教版数学九年级上册24.2.2 直线和圆的位置关系教学课件(第1课时 17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 338.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-05 00:00:00 | ||
图片预览






文档简介
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第1课时)
学习目标
学习目标
1.经历探索直线与圆的位置关系的过程.
2.理解直线与圆有相交、相切、相离三种位置关系.
把太阳看作一个圆,地平线看作一条直线
直线和圆的位置关系?
创设情境,引入新课
合作探究,形成新知
在纸上画一条直线l,把钥匙环看作一个圆,在纸上移动钥匙环.在这个过程中,圆与直线l的公共点个数的变化情况?
合作探究,形成新知
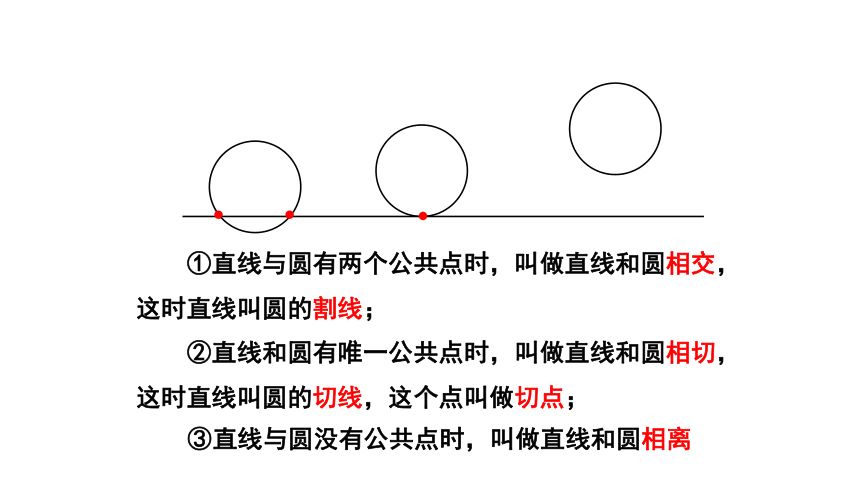
①直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线;
②直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫圆的切线,这个点叫做切点;
③直线与圆没有公共点时,叫做直线和圆相离
能否根据基本概念来判断直线与圆的位置关系?
直线l与⊙O没有公共点 直线l与⊙O相离.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O有两个公共点 直线l与⊙O相交.
合作探究,形成新知
能否根据点和圆的位置关系类似地推导出直线与圆的位置关系?
设⊙O的半径为r,直线l 到圆心O的距离为d,在直线和圆的不同位置关系中,d与r具有怎样的大小关系?反过来,你能根据d与r的大小关系来确定直线和圆的位置关系吗?
合作探究,形成新知
d=r 直线l 与⊙O相切;
d>r 直线l 与⊙O相离;
d<r 直线l 与⊙O相交.
d 表示圆心O到直线l 的距离,r表示⊙O的半径.
r
d
l
O
l
r
d
O
A
r
d
O
A
l
B
合作探究,形成新知
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
例题分析,深化提高
解 : (1) d=4.5 cm< r = 6.5 cm 直线与圆相交,
有两个公共点;
例题分析,深化提高
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
有一个公共点;
(2)d=6.5 cm = r = 6.5 cm 直线与圆相切,
例题分析,深化提高
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
(3)d=8 cm>r = 6.5 cm 直线与圆相离,
没有公共点.
例题分析,深化提高
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
练习巩固,综合应用
1.已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,2 cm长为半径的圆和AB的位置关系是_________;
(2)以C为圆心,4 cm长为半径的圆和AB的位置关系是_________;
(3)如果以C为圆心的圆和AB相切,则半径长为_________.
相离
相交
cm
2.Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,判断以点C为圆心,下列r为半径的⊙C与AB的位置关系:
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
练习巩固,综合应用
解:由题意,利用勾股定理可得AB=5 cm,由此可得(1)相离;(2)相切;(3)相交.
2.识别直线和圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线 l 和⊙O 没有公共点 直线 l 和⊙O 相离;
直线 l 和⊙O 只有一个公共点 直线 l 和⊙O 相切;
直线 l 和⊙O 有两个公共点 直线 l 和⊙O 相交.
1.直线和圆的位置关系有三种:相离、相切和相交.
课堂小结
2.识别直线和圆的位置关系的方法:
(2)另一种是根据圆心到直线的距离 d 与圆半径
r 的大小关系来进行识别:
d >r 直线 l 和⊙O 相离;
d =r 直线 l 和⊙O 相切;
d <r 直线 l 和⊙O 相交.
课堂小结
再见
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第1课时)
学习目标
学习目标
1.经历探索直线与圆的位置关系的过程.
2.理解直线与圆有相交、相切、相离三种位置关系.
把太阳看作一个圆,地平线看作一条直线
直线和圆的位置关系?
创设情境,引入新课
合作探究,形成新知
在纸上画一条直线l,把钥匙环看作一个圆,在纸上移动钥匙环.在这个过程中,圆与直线l的公共点个数的变化情况?
合作探究,形成新知
①直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线;
②直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫圆的切线,这个点叫做切点;
③直线与圆没有公共点时,叫做直线和圆相离
能否根据基本概念来判断直线与圆的位置关系?
直线l与⊙O没有公共点 直线l与⊙O相离.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O有两个公共点 直线l与⊙O相交.
合作探究,形成新知
能否根据点和圆的位置关系类似地推导出直线与圆的位置关系?
设⊙O的半径为r,直线l 到圆心O的距离为d,在直线和圆的不同位置关系中,d与r具有怎样的大小关系?反过来,你能根据d与r的大小关系来确定直线和圆的位置关系吗?
合作探究,形成新知
d=r 直线l 与⊙O相切;
d>r 直线l 与⊙O相离;
d<r 直线l 与⊙O相交.
d 表示圆心O到直线l 的距离,r表示⊙O的半径.
r
d
l
O
l
r
d
O
A
r
d
O
A
l
B
合作探究,形成新知
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
例题分析,深化提高
解 : (1) d=4.5 cm< r = 6.5 cm 直线与圆相交,
有两个公共点;
例题分析,深化提高
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
有一个公共点;
(2)d=6.5 cm = r = 6.5 cm 直线与圆相切,
例题分析,深化提高
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
(3)d=8 cm>r = 6.5 cm 直线与圆相离,
没有公共点.
例题分析,深化提高
A
B
·
6.5 cm
d=4.5 cm
O
M
·
N
O
6.5 cm
d=6.5 cm
D
·
O
6.5cm
d=8 cm
圆的直径是13 cm,如果直线与圆心的距离分别是(1)4.5 cm ; (2) 6.5 cm ;(3)8 cm,那么直线与圆分别是什么位置关系?有几个公共点?
练习巩固,综合应用
1.已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,2 cm长为半径的圆和AB的位置关系是_________;
(2)以C为圆心,4 cm长为半径的圆和AB的位置关系是_________;
(3)如果以C为圆心的圆和AB相切,则半径长为_________.
相离
相交
cm
2.Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,判断以点C为圆心,下列r为半径的⊙C与AB的位置关系:
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
练习巩固,综合应用
解:由题意,利用勾股定理可得AB=5 cm,由此可得(1)相离;(2)相切;(3)相交.
2.识别直线和圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线 l 和⊙O 没有公共点 直线 l 和⊙O 相离;
直线 l 和⊙O 只有一个公共点 直线 l 和⊙O 相切;
直线 l 和⊙O 有两个公共点 直线 l 和⊙O 相交.
1.直线和圆的位置关系有三种:相离、相切和相交.
课堂小结
2.识别直线和圆的位置关系的方法:
(2)另一种是根据圆心到直线的距离 d 与圆半径
r 的大小关系来进行识别:
d >r 直线 l 和⊙O 相离;
d =r 直线 l 和⊙O 相切;
d <r 直线 l 和⊙O 相交.
课堂小结
再见
同课章节目录
