北师大版七年级上册数学 综合与实践 3、制作一个尽可能大的无盖长方体形盒子 课件(18张)
文档属性
| 名称 | 北师大版七年级上册数学 综合与实践 3、制作一个尽可能大的无盖长方体形盒子 课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 16:41:04 | ||
图片预览


文档简介
综合实践
制作一个尽可能大的无盖长方体形盒子
北师大版数学七年级(上册)
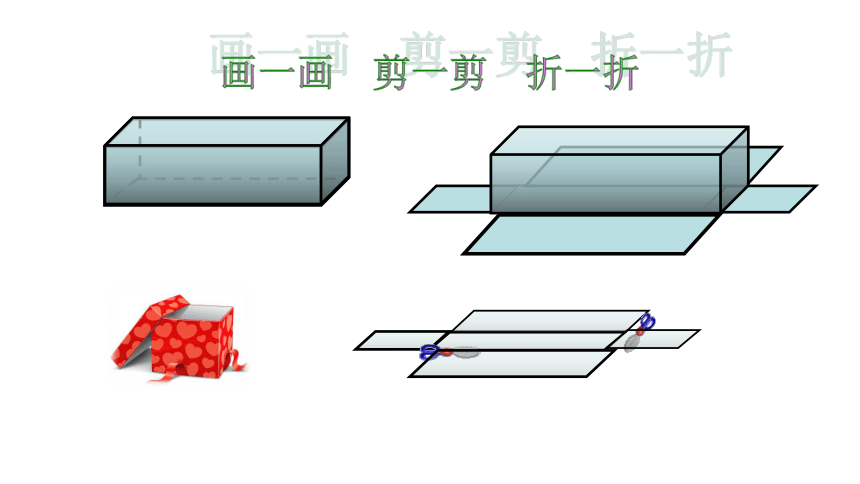
六一临近,张老师正为班里缺少用来盛放瓜子的长方体形盒子而发愁。现有一定数量的正方形纸想做成无盖的长方体盒子盛瓜子,要求容积最大。现在请同学们设计出合理的方案,并制作出模型。聪明的同学们,你能帮助他设计一下吗?
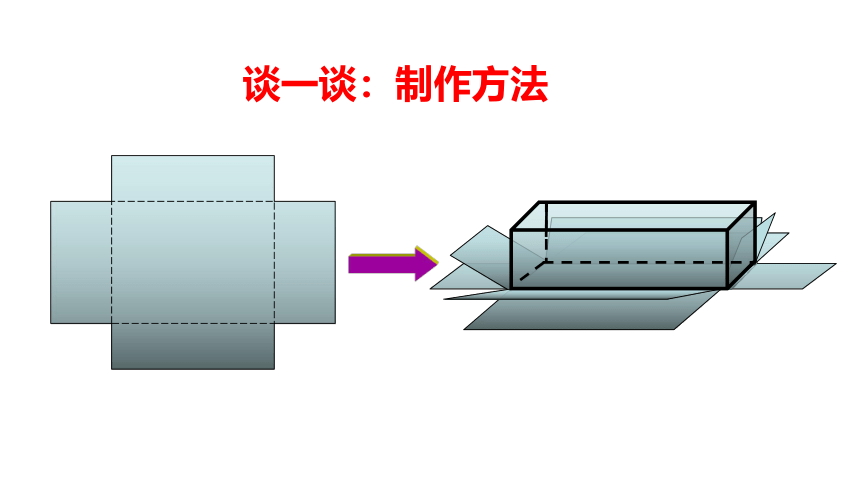
谈一谈:制作方法
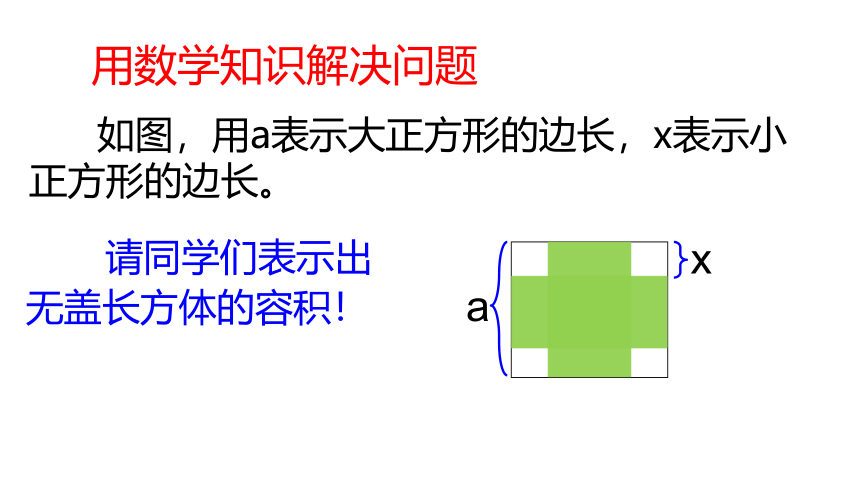
用数学知识解决问题
如图,用a表示大正方形的边长,x表示小正方形的边长。
请同学们表示出无盖长方体的容积!
a
x
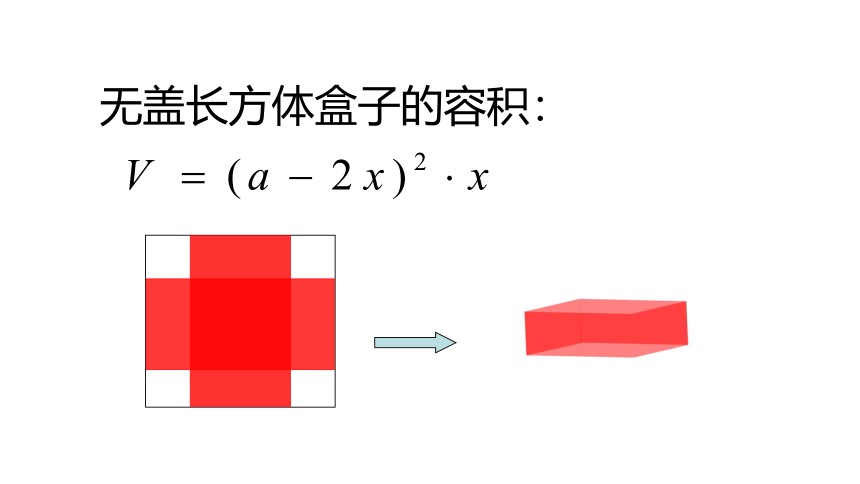
无盖长方体盒子的容积:
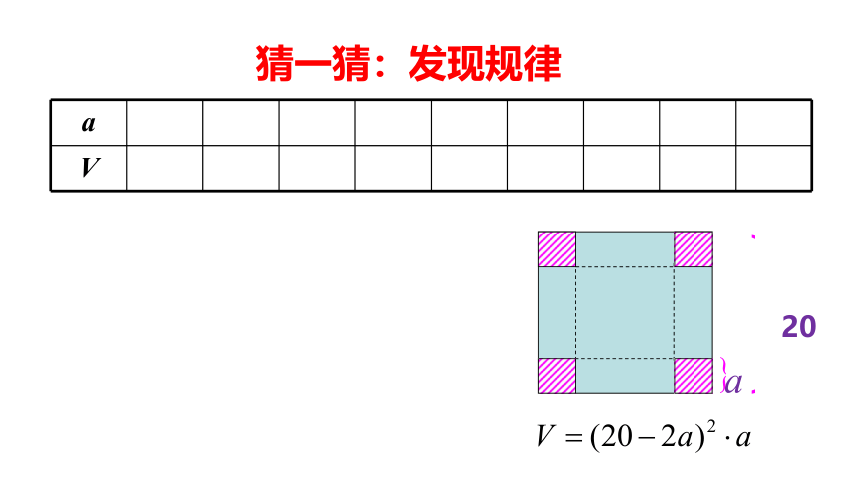
猜一猜:发现规律
a
V
20
a
a
V
a
1
2
3
4
5
6
7
8
9
V
猜一猜:发现规律
20
a
a
1
2
3
4
5
6
7
8
9
V
猜一猜:发现规律
a
V
324
512
588
576
500
384
252
128
36
20
a
猜一猜:发现规律
a
1
2
3
4
5
6
7
8
9
V
324
512
588
576
500
384
252
128
36
20
a
当a=20时,试求 的最大值。
进一步确定x的取值范围:
x
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
v
当a=20时,试求 的最大值。
x
3.31
3.32
3.33
3.34
3.35
v
x
3.36
3.37
3.38
3.39
…
v
由此我们可以猜想:
当a=20时,x取何值时V的值最大呢?
我们可以发现:当x= 时,V有最大值
通过我们刚刚的探索你能发现什么呢?
x与a有什么关系呢?
结论:当x= 时, 有最大值。
V的最大值为
上面我们用了“夹逼”的方法得出了这个结论。
当a=9或10时,x取何值V的值最大?
各小组互相协作完成
当a=9时,x= 1.5 V的值最大
当a=10时,x=
V的值最大
用一块正方形纸板如何制做一个最大的长方体盒子呢?
1、量出正方形的边长a并计算出
2、然后在正方形的四个角上截取边长为 的四个小正方形
制作方法:
你的疑问、你的收获、你的想法!
数学思维方法:
实际问题
数学模型
数学问题
猜想
验证
归纳
制作一个尽可能大的无盖长方体形盒子
北师大版数学七年级(上册)
六一临近,张老师正为班里缺少用来盛放瓜子的长方体形盒子而发愁。现有一定数量的正方形纸想做成无盖的长方体盒子盛瓜子,要求容积最大。现在请同学们设计出合理的方案,并制作出模型。聪明的同学们,你能帮助他设计一下吗?
谈一谈:制作方法
用数学知识解决问题
如图,用a表示大正方形的边长,x表示小正方形的边长。
请同学们表示出无盖长方体的容积!
a
x
无盖长方体盒子的容积:
猜一猜:发现规律
a
V
20
a
a
V
a
1
2
3
4
5
6
7
8
9
V
猜一猜:发现规律
20
a
a
1
2
3
4
5
6
7
8
9
V
猜一猜:发现规律
a
V
324
512
588
576
500
384
252
128
36
20
a
猜一猜:发现规律
a
1
2
3
4
5
6
7
8
9
V
324
512
588
576
500
384
252
128
36
20
a
当a=20时,试求 的最大值。
进一步确定x的取值范围:
x
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
v
当a=20时,试求 的最大值。
x
3.31
3.32
3.33
3.34
3.35
v
x
3.36
3.37
3.38
3.39
…
v
由此我们可以猜想:
当a=20时,x取何值时V的值最大呢?
我们可以发现:当x= 时,V有最大值
通过我们刚刚的探索你能发现什么呢?
x与a有什么关系呢?
结论:当x= 时, 有最大值。
V的最大值为
上面我们用了“夹逼”的方法得出了这个结论。
当a=9或10时,x取何值V的值最大?
各小组互相协作完成
当a=9时,x= 1.5 V的值最大
当a=10时,x=
V的值最大
用一块正方形纸板如何制做一个最大的长方体盒子呢?
1、量出正方形的边长a并计算出
2、然后在正方形的四个角上截取边长为 的四个小正方形
制作方法:
你的疑问、你的收获、你的想法!
数学思维方法:
实际问题
数学模型
数学问题
猜想
验证
归纳
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
