人教版八年级上册数学12.2全等三角形的判定-边边边课件(20张)
文档属性
| 名称 | 人教版八年级上册数学12.2全等三角形的判定-边边边课件(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览





文档简介
12.2.4 全等三角形的判定
SSS(边边边定理)
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
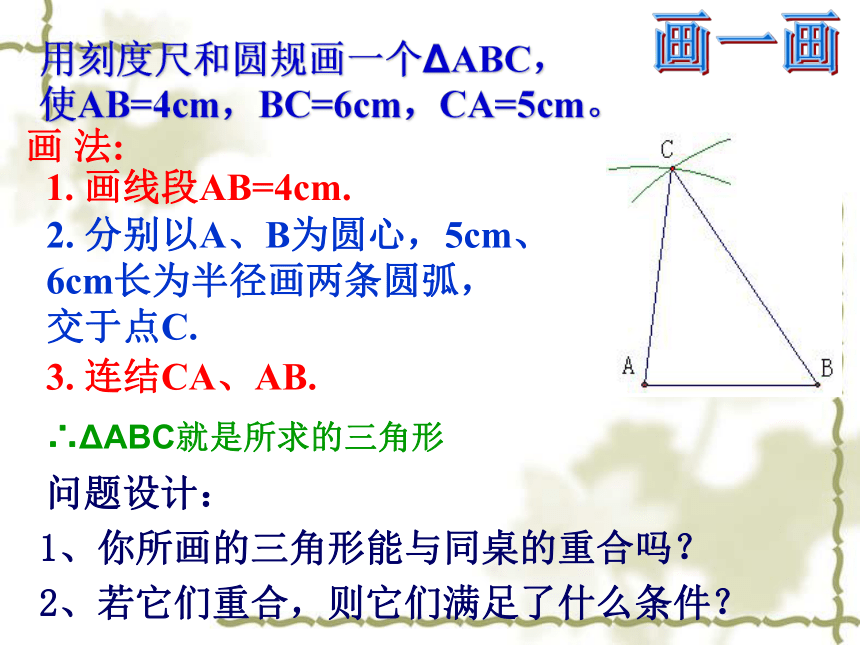
用刻度尺和圆规画一个ΔABC,
使AB=4cm,BC=6cm,CA=5cm。
1. 画线段AB=4cm.
画 法:
2. 分别以A、B为圆心,5cm、
6cm长为半径画两条圆弧,
交于点C.
3. 连结CA、AB.
问题设计:
1、你所画的三角形能与同桌的重合吗?
2、若它们重合,则它们满足了什么条件?
∴ΔABC就是所求的三角形
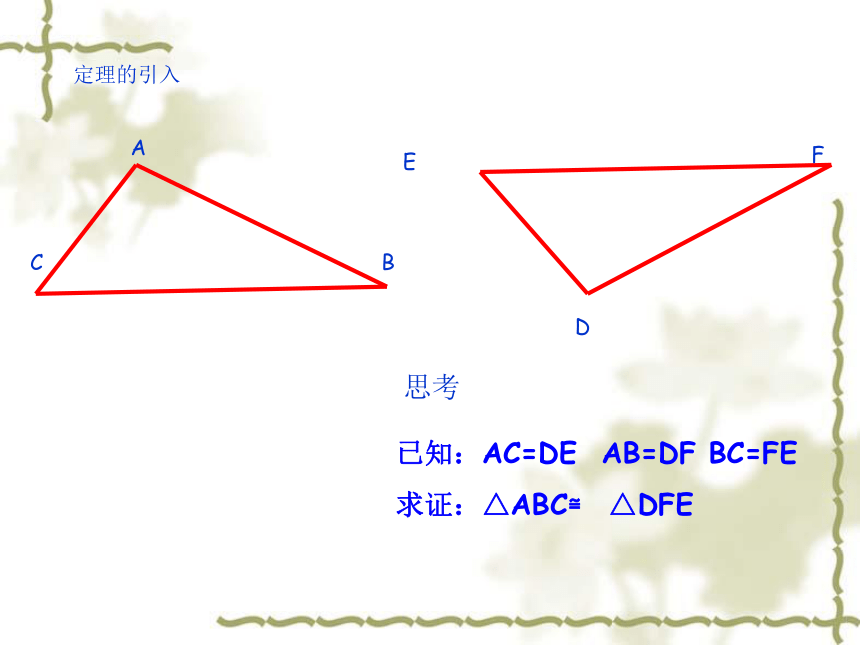
定理的引入
A
B
C
D
已知:AC=DE AB=DF BC=FE
求证:△ABC≌ △DFE
E
思考
F
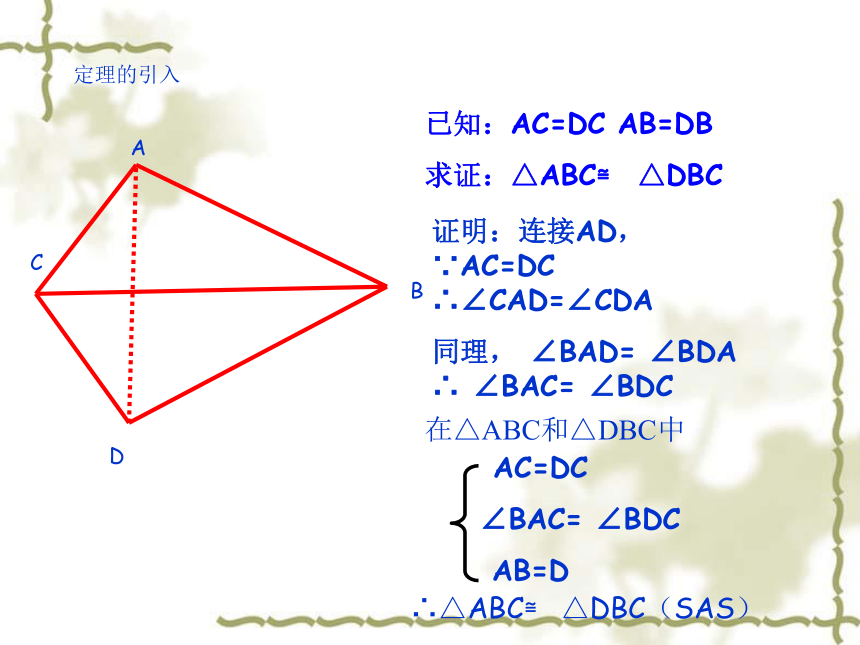
定理的引入
A
B
C
D
已知:AC=DC AB=DB
求证:△ABC≌ △DBC
证明:连接AD, ∵AC=DC ∴∠CAD=∠CDA
同理, ∠BAD= ∠BDA ∴ ∠BAC= ∠BDC
AC=DC
∠BAC= ∠BDC
AB=D
∴△ABC≌ △DBC(SAS)
在△ABC和△DBC中
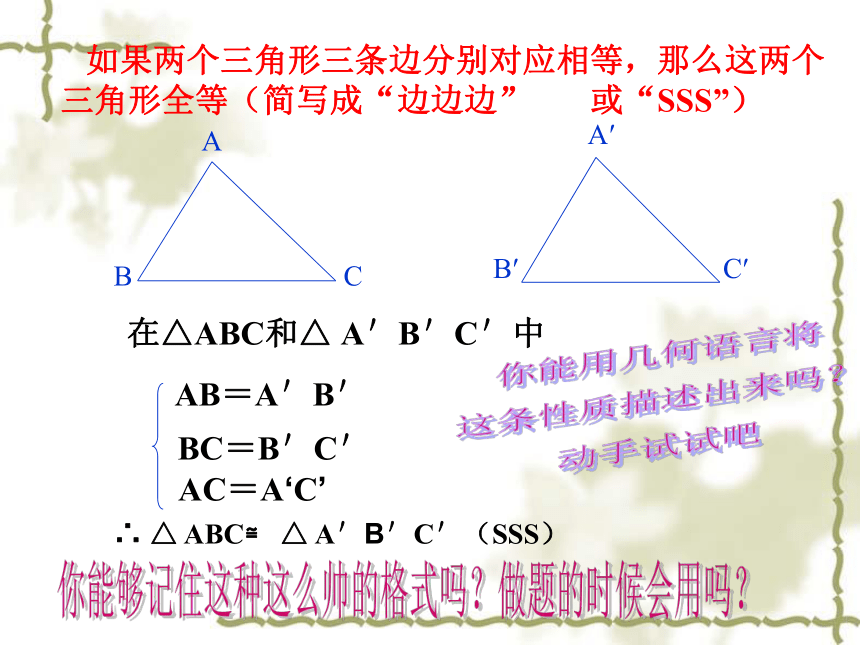
如果两个三角形三条边分别对应相等,那么这两个三角形全等(简写成“边边边” 或“SSS”)
A
B
C
A′
B′
C′
AB=A'B'
AC=A‘C’
BC=B'C'
∴ △ ABC≌ △ A'B'C'(SSS)
在△ABC和△ A'B'C'中
解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
= ( )
∴ △ABC ≌ ( )
BC
CB
△DCB
A
B
C
D
尝试练习:
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?
试说明理由。
公共边
SSS
在△ABC和△DCB中
练习:如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。试说明∠A=∠D的理由。
∵BE=CF(已知)
即 BC=EF
在△ABC和△DEF中
AB=DE(已知)
AC=BF(已知)
BC=EF(已证)
∴△ABC≌△DEF(SSS)
∴∠A=∠D(全等三角形对应角相等)
F
A
B
E
C
D
∴ BE+EC=CF+EC
证明:
例1、如图,已知AB=CD,AD=CB,
试说明∠B=∠D的理由
证明:连结AC
∴ ∠B=∠D(全等三角形对应角相等)
A
B
C
D
A
B
C
D
AB=CD(已知)
AC=CA(公共边)
CB=AD(已知)
∴ △ ABC≌ △ CDA(SSS)
在△ABC和△ CDA中
小结:要说明两个角相等,可以利用它们所在的两个三角形全等的性质来说明。
新知运用
能说明∠A=∠C吗?
自主
合作
探究
互动
如图,小明在做数学作业时,遇到这样一个问题:
AB=CD,BC=AD,请说明∠A=∠C的道理。小明
动手测量了一下,发现∠A确实与∠C相等,但他
不能说明其中的道理,你能帮助他吗?
A
C
B
O
D
在△ABD和△CDB中,
证明:连接BD
AB=CD
BC=AD
BD=BD
∴
△ABD≌△CDB(S.S.S.)
拓展:如图
已知:AB=AC,AE是角平分线。试问图中有对全等三角形?
E
答:图中有△ABE≌ACE,
△ABD≌ACD。△BDE≌CDE
AB=AC( 已知)
∠1=∠2(角平分线)
AE=AE(公共边)
∴ △ABE≌ACE( )
(1)
(2)
AB=AC( 已知)
∠1=∠2(角平分线)
AD=AD(公共边)
∴ △ABD≌ACD( )
(3)
BE=CE
BD=CD(等腰三角形三线合一)
ED=ED(公共边)
∴ △BDE≌CDE ( )
在△ABE和△ ACE中
在△ABD和△ ACD中
在△ABD和△ ACD中
∵ △ABE≌ACD
∴ BE=CE
SAS
SAS
SSS
作业:课后习题
A
B
C
A’
B’
C’
AB=A’B’
∠A=∠A’
AC=A’C’
ΔABC ≌ ?A’ B’ C’(SAS)
在△ABC和△ A'B'C'中
A
B
C
A’
B’
C’
∠A=∠A’
AB=A’B’
∠B=∠B’
ΔABC ≌ ?A’ B’ C’(ASA)
在△ABC和△ A'B'C'中
A
B
C
A’
B’
C’
∠A=∠A’
∠B=∠B’
AC=A’C’
ΔABC ≌ ?A’ B’ C’(AAS)
在△ABC和△ A'B'C'中
总结
上题中应用了哪些性质及定理
性质一:等腰三角形的两底角相等
性质二:等腰三角形的中线、角平分线、高线互相重合。
定理三:在两个三角形中,如果有三条边相等,那么这两个三角形全等。
定理四:在两个三角形中,如果有两个角相等及一条边相等,那么这两个三角形全等。
定理五:在两个三角形中,如果有两个角相等及所夹的边相等,那么这两个三角形全等。
定理六:在两个三角形中,如果有两条边相等及所夹的角相等,那么这两个三角形全等。
回顾
SAS 定理:在两个三角形中,如果有两条边相等及其夹角相等,那么这两个三角形全等。(边角边定理)
AAS定理:在两个三角形中,如果有两个角相等及其一条边相等,那么这两个三角形全等。(角角边定理)
ASA定理:在两个三角形中,如果有两个角相等及其夹边相等,那么这两个三角形全等。(角边角定理)
SSS(边边边定理)
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
(3) 三角形的三个角对应相等。
三个条件
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
(2) 三角形的两个角和一条边对应相等。
①两角及夹边 ②两角和其中一角的对边
(4) 三角形的三条边对应相等。
三角形的两条边和一个角对应相等。
①两边及夹角 ②两边和其中一边的对角
SAS
ASA
?
AAS
用刻度尺和圆规画一个ΔABC,
使AB=4cm,BC=6cm,CA=5cm。
1. 画线段AB=4cm.
画 法:
2. 分别以A、B为圆心,5cm、
6cm长为半径画两条圆弧,
交于点C.
3. 连结CA、AB.
问题设计:
1、你所画的三角形能与同桌的重合吗?
2、若它们重合,则它们满足了什么条件?
∴ΔABC就是所求的三角形
定理的引入
A
B
C
D
已知:AC=DE AB=DF BC=FE
求证:△ABC≌ △DFE
E
思考
F
定理的引入
A
B
C
D
已知:AC=DC AB=DB
求证:△ABC≌ △DBC
证明:连接AD, ∵AC=DC ∴∠CAD=∠CDA
同理, ∠BAD= ∠BDA ∴ ∠BAC= ∠BDC
AC=DC
∠BAC= ∠BDC
AB=D
∴△ABC≌ △DBC(SAS)
在△ABC和△DBC中
如果两个三角形三条边分别对应相等,那么这两个三角形全等(简写成“边边边” 或“SSS”)
A
B
C
A′
B′
C′
AB=A'B'
AC=A‘C’
BC=B'C'
∴ △ ABC≌ △ A'B'C'(SSS)
在△ABC和△ A'B'C'中
解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
= ( )
∴ △ABC ≌ ( )
BC
CB
△DCB
A
B
C
D
尝试练习:
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?
试说明理由。
公共边
SSS
在△ABC和△DCB中
练习:如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。试说明∠A=∠D的理由。
∵BE=CF(已知)
即 BC=EF
在△ABC和△DEF中
AB=DE(已知)
AC=BF(已知)
BC=EF(已证)
∴△ABC≌△DEF(SSS)
∴∠A=∠D(全等三角形对应角相等)
F
A
B
E
C
D
∴ BE+EC=CF+EC
证明:
例1、如图,已知AB=CD,AD=CB,
试说明∠B=∠D的理由
证明:连结AC
∴ ∠B=∠D(全等三角形对应角相等)
A
B
C
D
A
B
C
D
AB=CD(已知)
AC=CA(公共边)
CB=AD(已知)
∴ △ ABC≌ △ CDA(SSS)
在△ABC和△ CDA中
小结:要说明两个角相等,可以利用它们所在的两个三角形全等的性质来说明。
新知运用
能说明∠A=∠C吗?
自主
合作
探究
互动
如图,小明在做数学作业时,遇到这样一个问题:
AB=CD,BC=AD,请说明∠A=∠C的道理。小明
动手测量了一下,发现∠A确实与∠C相等,但他
不能说明其中的道理,你能帮助他吗?
A
C
B
O
D
在△ABD和△CDB中,
证明:连接BD
AB=CD
BC=AD
BD=BD
∴
△ABD≌△CDB(S.S.S.)
拓展:如图
已知:AB=AC,AE是角平分线。试问图中有对全等三角形?
E
答:图中有△ABE≌ACE,
△ABD≌ACD。△BDE≌CDE
AB=AC( 已知)
∠1=∠2(角平分线)
AE=AE(公共边)
∴ △ABE≌ACE( )
(1)
(2)
AB=AC( 已知)
∠1=∠2(角平分线)
AD=AD(公共边)
∴ △ABD≌ACD( )
(3)
BE=CE
BD=CD(等腰三角形三线合一)
ED=ED(公共边)
∴ △BDE≌CDE ( )
在△ABE和△ ACE中
在△ABD和△ ACD中
在△ABD和△ ACD中
∵ △ABE≌ACD
∴ BE=CE
SAS
SAS
SSS
作业:课后习题
A
B
C
A’
B’
C’
AB=A’B’
∠A=∠A’
AC=A’C’
ΔABC ≌ ?A’ B’ C’(SAS)
在△ABC和△ A'B'C'中
A
B
C
A’
B’
C’
∠A=∠A’
AB=A’B’
∠B=∠B’
ΔABC ≌ ?A’ B’ C’(ASA)
在△ABC和△ A'B'C'中
A
B
C
A’
B’
C’
∠A=∠A’
∠B=∠B’
AC=A’C’
ΔABC ≌ ?A’ B’ C’(AAS)
在△ABC和△ A'B'C'中
总结
上题中应用了哪些性质及定理
性质一:等腰三角形的两底角相等
性质二:等腰三角形的中线、角平分线、高线互相重合。
定理三:在两个三角形中,如果有三条边相等,那么这两个三角形全等。
定理四:在两个三角形中,如果有两个角相等及一条边相等,那么这两个三角形全等。
定理五:在两个三角形中,如果有两个角相等及所夹的边相等,那么这两个三角形全等。
定理六:在两个三角形中,如果有两条边相等及所夹的角相等,那么这两个三角形全等。
回顾
SAS 定理:在两个三角形中,如果有两条边相等及其夹角相等,那么这两个三角形全等。(边角边定理)
AAS定理:在两个三角形中,如果有两个角相等及其一条边相等,那么这两个三角形全等。(角角边定理)
ASA定理:在两个三角形中,如果有两个角相等及其夹边相等,那么这两个三角形全等。(角边角定理)
