人教版八年级上册数学12.2全等三角形判定定理课件(第一课时 26张 )
文档属性
| 名称 | 人教版八年级上册数学12.2全等三角形判定定理课件(第一课时 26张 ) |  | |
| 格式 | pptx | ||
| 文件大小 | 471.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 21:23:44 | ||
图片预览





文档简介
§12.2 三角形全等的
判定定理(一)
(第一课时)
教学目标:
2、掌握三角形全等的“边边边”条件及应用
1、探索两个三角形全等的条件
重 点:
判定两个三角形全等的"SSS"定理
难 点:
探索三角形全等条件及应用
教学方法:
探究学习、讲练结合
教具学具: 三角板或直尺、圆规
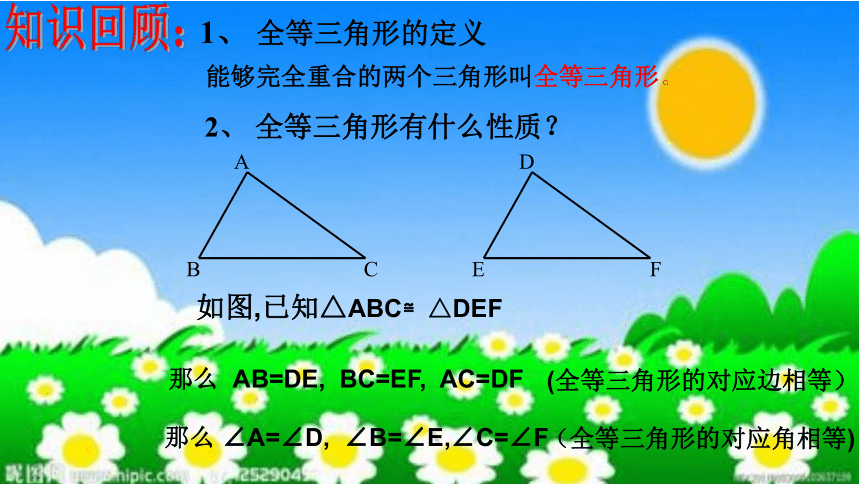
1、 全等三角形的定义
2、 全等三角形有什么性质?
知识回顾:
那么 AB=DE, BC=EF, AC=DF
那么 ∠A=∠D, ∠B=∠E,∠C=∠F
如图,已知△ABC≌△DEF
A
B
C
D
E
F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
能够完全重合的两个三角形叫全等三角形。
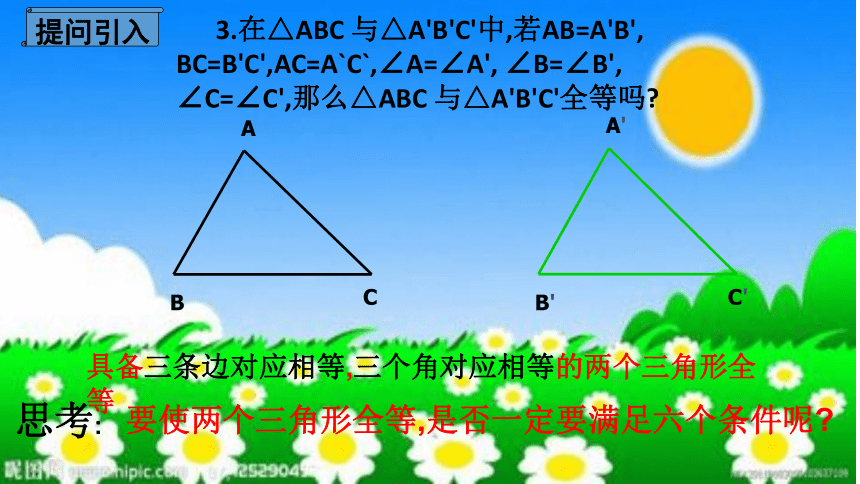
3.在△ABC 与△A'B'C'中,若AB=A'B',
BC=B'C',AC=A`C`,∠A=∠A', ∠B=∠B', ∠C=∠C',那么△ABC 与△A'B'C'全等吗?
具备三条边对应相等,三个角对应相等的两个三角形全等
A
B
C
A'
B'
C'
思考:
要使两个三角形全等,是否一定要满足六个条件呢?
提问引入
(1)一个条件
(2)两个条件
(3)三个条件
一边相等
一角相等
两边相等
两角相等
一边一角相等
三角相等
三边相等
两边一角相等
两角一边相等
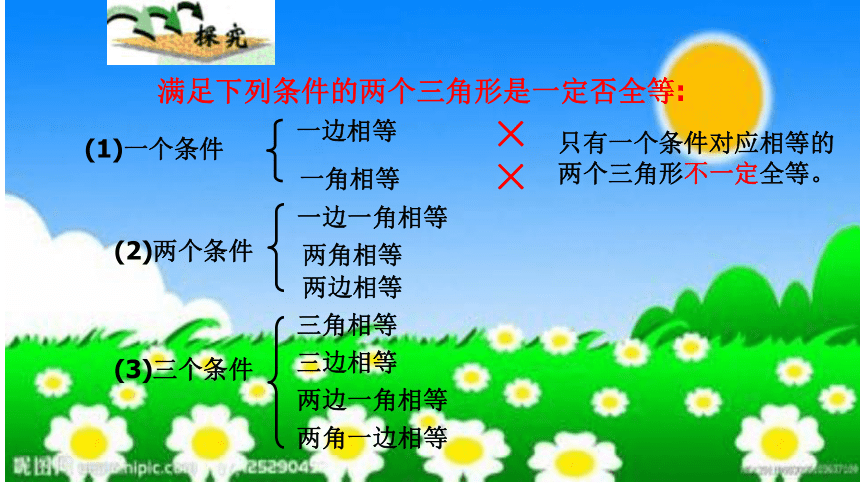
满足下列条件的两个三角形是否一定全等:
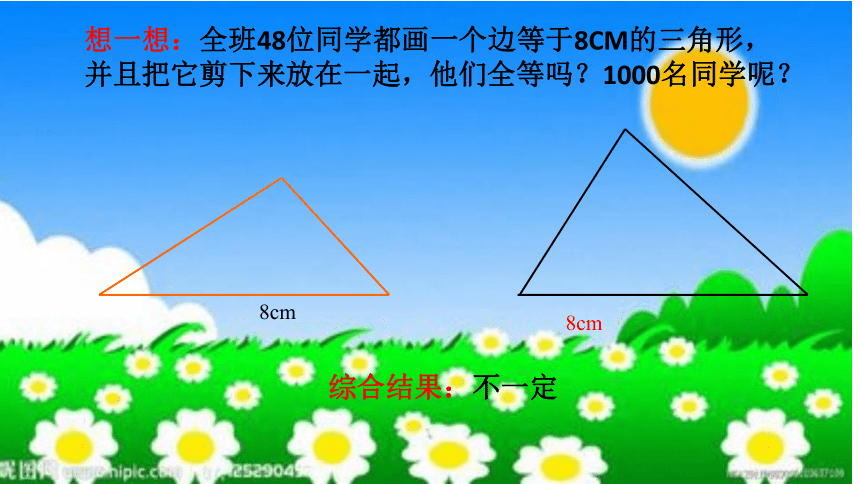
8cm
8cm
想一想:全班48位同学都画一个边等于8CM的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是否一定全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
(1)一个条件
(2)两个条件
(3)三个条件
400
400
想一想:全班48位同学都画一个角等于400的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
300
9cm
300
9cm
300
9cm
300
9cm
300
9cm
想一想:全班48位同学都画一个边等于9CM,角等于300的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
300
500
300
500
想一想:全班48位同学都画一个角分别等于300和500的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
(1)一个条件
(2)两个条件
(3)三个条件
8cm
9cm
8cm
9cm
想一想:全班48位同学都画一个边分别等于8CM和9CM的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一 定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
65度
35度
80度
65度
35度
80度
想一想:全班48位同学都画一个角分别等于35度、65度、80度的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一 定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
8cm
6cm
9cm
8cm
6cm
9cm
想一想:全班48位同学都画一个三边分别等于6CM、8CM、9CM的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:一 定
满足下列条件的两个三角形是否一定全等:
一个条件
两个条件
三个条件
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
三边相等的两个三角形一定全等
三边相等的两个三角形会全等吗?
画法:
动手试一试
你能得出什么结论?
课本P36
我们发现:两个三角形是全等的。
所以:三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS")
如下图,△ABC是一个钢架,AB=AC,AD是连
接A与BC中点D的支架。求证:△ABD≌△ACD
分析:要证明△ ABD≌ △ACD,首先要看这两个三角形的三条边是否对应相等。
证明: ∵D是BC中点,
∴BD=CD.
AB=AC,
BD=CD,
AD=AD,
∴ △ABD ≌△ ACD(SSS).
在△ABD和△ ACD中,
练一练:
B
注意:三角形全等的对应顶点要写在对应位置上。
如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。
C
A
B
D
E
练一练
在△AEB和△ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌△ ADC (sss)
证明:∵BD=CE
∴ BD-ED=CE-ED,
即BE=CD。
小 结
2. 掌握画一个三角形与另一个三角形全等的 方法。
1. 要理解三角形全等的推理过程及方法。
3. 学会利用“边边边”定理证明两个三角形 全等.
作业安排:
P37 练习 1 , 2
结 束 !
判定定理(一)
(第一课时)
教学目标:
2、掌握三角形全等的“边边边”条件及应用
1、探索两个三角形全等的条件
重 点:
判定两个三角形全等的"SSS"定理
难 点:
探索三角形全等条件及应用
教学方法:
探究学习、讲练结合
教具学具: 三角板或直尺、圆规
1、 全等三角形的定义
2、 全等三角形有什么性质?
知识回顾:
那么 AB=DE, BC=EF, AC=DF
那么 ∠A=∠D, ∠B=∠E,∠C=∠F
如图,已知△ABC≌△DEF
A
B
C
D
E
F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
能够完全重合的两个三角形叫全等三角形。
3.在△ABC 与△A'B'C'中,若AB=A'B',
BC=B'C',AC=A`C`,∠A=∠A', ∠B=∠B', ∠C=∠C',那么△ABC 与△A'B'C'全等吗?
具备三条边对应相等,三个角对应相等的两个三角形全等
A
B
C
A'
B'
C'
思考:
要使两个三角形全等,是否一定要满足六个条件呢?
提问引入
(1)一个条件
(2)两个条件
(3)三个条件
一边相等
一角相等
两边相等
两角相等
一边一角相等
三角相等
三边相等
两边一角相等
两角一边相等
满足下列条件的两个三角形是否一定全等:
8cm
8cm
想一想:全班48位同学都画一个边等于8CM的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是否一定全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
(1)一个条件
(2)两个条件
(3)三个条件
400
400
想一想:全班48位同学都画一个角等于400的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
300
9cm
300
9cm
300
9cm
300
9cm
300
9cm
想一想:全班48位同学都画一个边等于9CM,角等于300的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
300
500
300
500
想一想:全班48位同学都画一个角分别等于300和500的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
(1)一个条件
(2)两个条件
(3)三个条件
8cm
9cm
8cm
9cm
想一想:全班48位同学都画一个边分别等于8CM和9CM的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一 定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
(1)一个条件
(2)两个条件
(3)三个条件
65度
35度
80度
65度
35度
80度
想一想:全班48位同学都画一个角分别等于35度、65度、80度的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:不一 定
满足下列条件的两个三角形是一定否全等:
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
(1)一个条件
(2)两个条件
(3)三个条件
8cm
6cm
9cm
8cm
6cm
9cm
想一想:全班48位同学都画一个三边分别等于6CM、8CM、9CM的三角形,并且把它剪下来放在一起,他们全等吗?1000名同学呢?
综合结果:一 定
满足下列条件的两个三角形是否一定全等:
一个条件
两个条件
三个条件
一边相等
一角相等
两边相等
一边一角相等
两角相等
三角相等
三边相等
两边一角相等
两角一边相等
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
三边相等的两个三角形一定全等
三边相等的两个三角形会全等吗?
画法:
动手试一试
你能得出什么结论?
课本P36
我们发现:两个三角形是全等的。
所以:三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS")
如下图,△ABC是一个钢架,AB=AC,AD是连
接A与BC中点D的支架。求证:△ABD≌△ACD
分析:要证明△ ABD≌ △ACD,首先要看这两个三角形的三条边是否对应相等。
证明: ∵D是BC中点,
∴BD=CD.
AB=AC,
BD=CD,
AD=AD,
∴ △ABD ≌△ ACD(SSS).
在△ABD和△ ACD中,
练一练:
B
注意:三角形全等的对应顶点要写在对应位置上。
如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。
C
A
B
D
E
练一练
在△AEB和△ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌△ ADC (sss)
证明:∵BD=CE
∴ BD-ED=CE-ED,
即BE=CD。
小 结
2. 掌握画一个三角形与另一个三角形全等的 方法。
1. 要理解三角形全等的推理过程及方法。
3. 学会利用“边边边”定理证明两个三角形 全等.
作业安排:
P37 练习 1 , 2
结 束 !
