人教版八年级数学上册 11.2.2 三角形的外角 课件(第三课时 19张)
文档属性
| 名称 | 人教版八年级数学上册 11.2.2 三角形的外角 课件(第三课时 19张) |  | |
| 格式 | zip | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 21:44:01 | ||
图片预览



文档简介
(共19张PPT)
11.2
与三角形有关的角
第3课时
2、在ABC中,
(1)∠C=90°,∠A=30
°,则∠B=
;
(2)∠A=50
°,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4,则∠A= ,
∠B=
,∠C=
.
40°
60°
80°
65°
60°
三角形的内角和等于180度
创设情景
明确目标
A
B
C
D
E
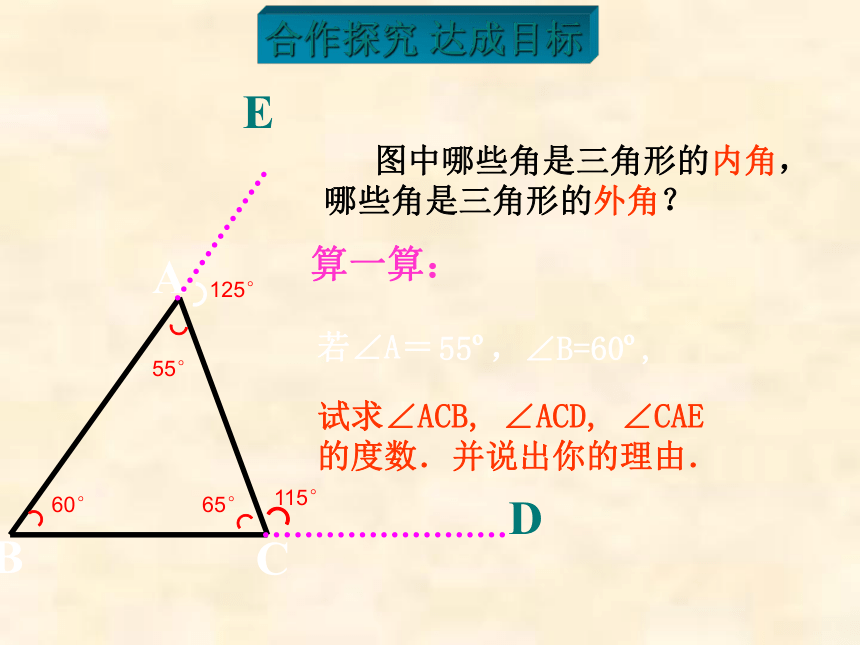
算一算:
若∠A=
55?,∠B=60?,
试求∠ACB,
∠ACD,
∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
合作探究
达成目标
通过上题的计算,你发现∠ACD,∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
结论:
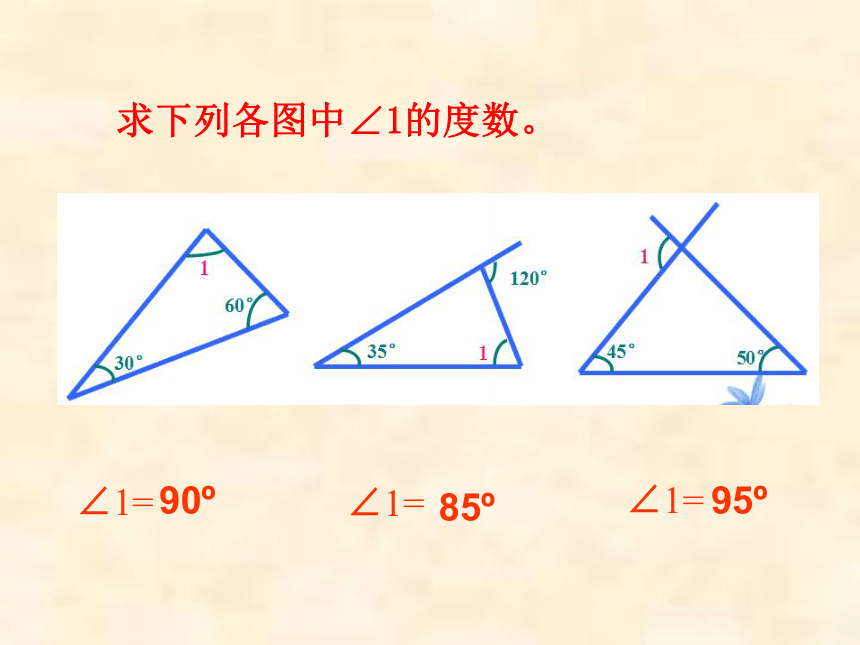
求下列各图中∠1的度数。
∠1=
∠1=
∠1=
90?
85?
95?
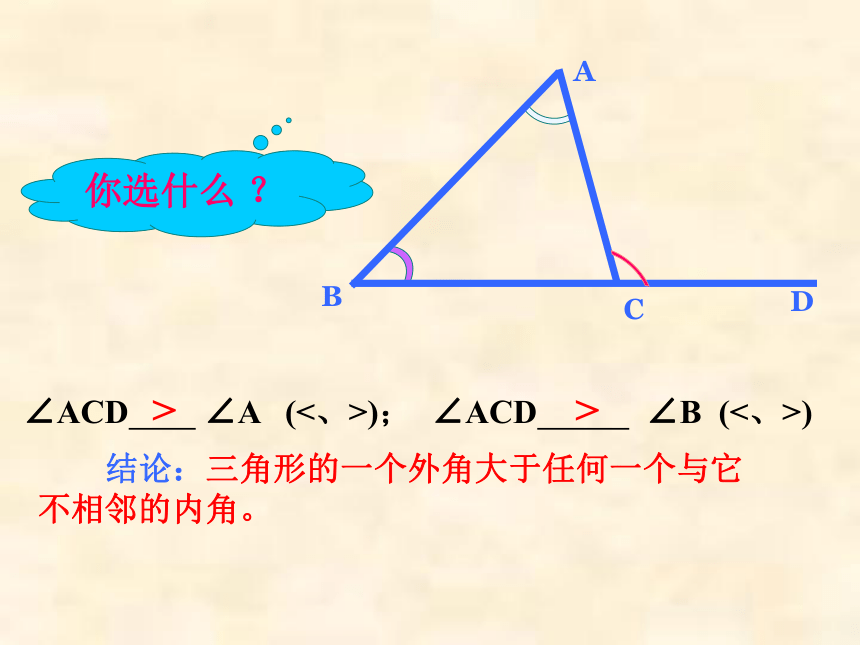
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
你选什么
?
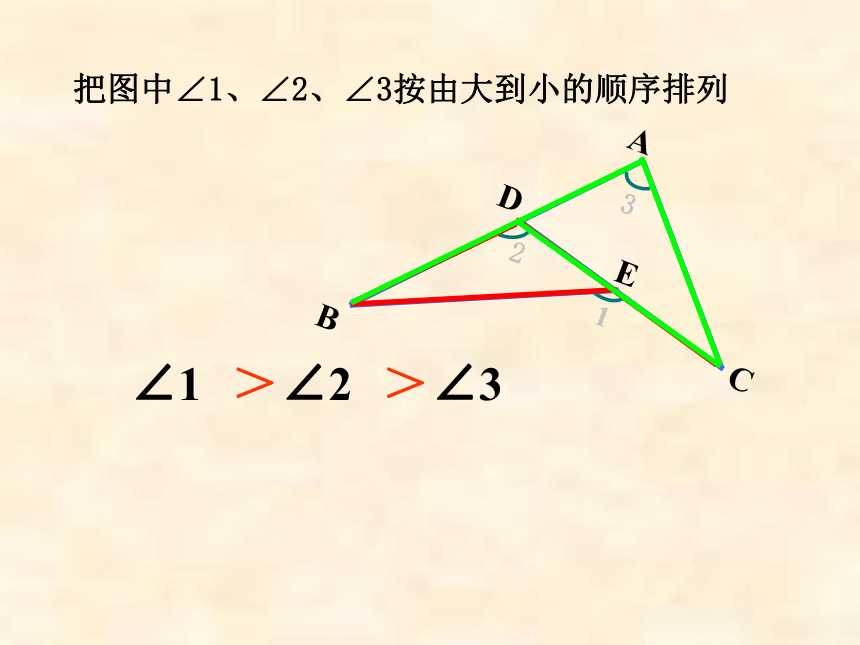
把图中∠1、∠2、∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
A
B
C
1
2
3
三角形的外角和等于360°
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果
探究点二
三角形外角的性质
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
方法1
解:过A作AD平行于BC
∴
∠3=
∠4
B
C
1
2
3
4
A
∴
∠2=
∠BAD
∴
∠1+
∠2+
∠3=
∠1+
∠BAD+
∠4=360°
两直线平行,同位角相等
D
方法2
例:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
40?
40?
70?
1、三角形外角的两条性质
①
三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360°
总结梳理
内化目标
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。(
)
达标检测
反思目标
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
1
2
3
360°
N
P
M
A
B
C
D
E
求∠A+
∠B+
∠C+
∠D+
∠E的度数
⌒
F
G
⌒
∠B+
∠D=
∠EGF
∠EGF
+
∠EFG
+
∠E
=
180°
∠A+
∠C=
∠EFG
解:因为
所以
∠A+
∠B+
∠C+
∠D+
∠E=
180°
已知图中∠A、∠B、∠C分别为80°,20°,30°,求∠1的度数。
如图,试计算∠BOC的度数.
A
B
C
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
上交作业:
教科书第17页
第5,6,8,11题
.
课后作业:同步练习册相应习题.
课后作业
11.2
与三角形有关的角
第3课时
2、在ABC中,
(1)∠C=90°,∠A=30
°,则∠B=
;
(2)∠A=50
°,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4,则∠A= ,
∠B=
,∠C=
.
40°
60°
80°
65°
60°
三角形的内角和等于180度
创设情景
明确目标
A
B
C
D
E
算一算:
若∠A=
55?,∠B=60?,
试求∠ACB,
∠ACD,
∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
合作探究
达成目标
通过上题的计算,你发现∠ACD,∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
结论:
求下列各图中∠1的度数。
∠1=
∠1=
∠1=
90?
85?
95?
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
你选什么
?
把图中∠1、∠2、∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
A
B
C
1
2
3
三角形的外角和等于360°
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果
探究点二
三角形外角的性质
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
方法1
解:过A作AD平行于BC
∴
∠3=
∠4
B
C
1
2
3
4
A
∴
∠2=
∠BAD
∴
∠1+
∠2+
∠3=
∠1+
∠BAD+
∠4=360°
两直线平行,同位角相等
D
方法2
例:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
40?
40?
70?
1、三角形外角的两条性质
①
三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360°
总结梳理
内化目标
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。(
)
达标检测
反思目标
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
1
2
3
360°
N
P
M
A
B
C
D
E
求∠A+
∠B+
∠C+
∠D+
∠E的度数
⌒
F
G
⌒
∠B+
∠D=
∠EGF
∠EGF
+
∠EFG
+
∠E
=
180°
∠A+
∠C=
∠EFG
解:因为
所以
∠A+
∠B+
∠C+
∠D+
∠E=
180°
已知图中∠A、∠B、∠C分别为80°,20°,30°,求∠1的度数。
如图,试计算∠BOC的度数.
A
B
C
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
上交作业:
教科书第17页
第5,6,8,11题
.
课后作业:同步练习册相应习题.
课后作业
