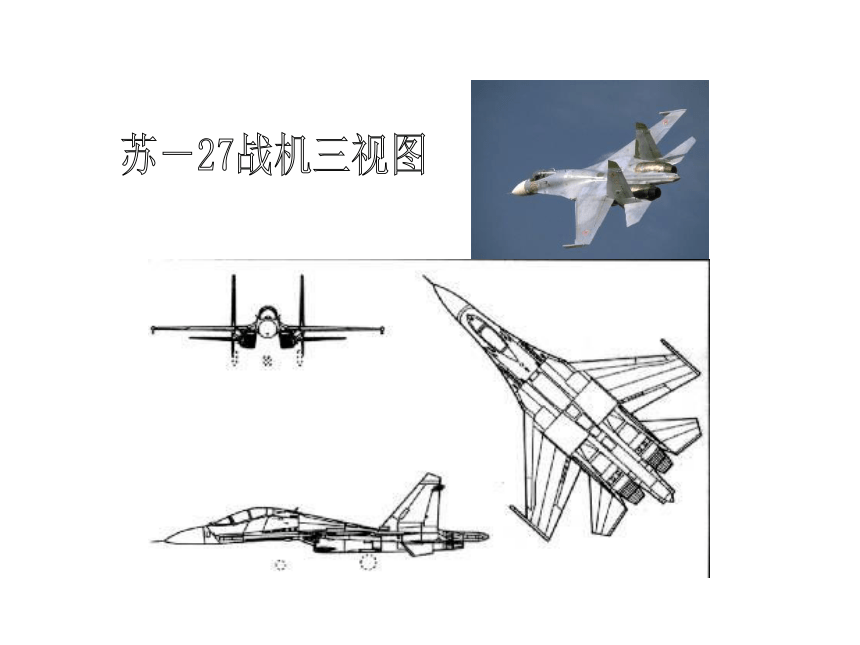
4-1三视图的画法
图片预览




文档简介
(共40张PPT)
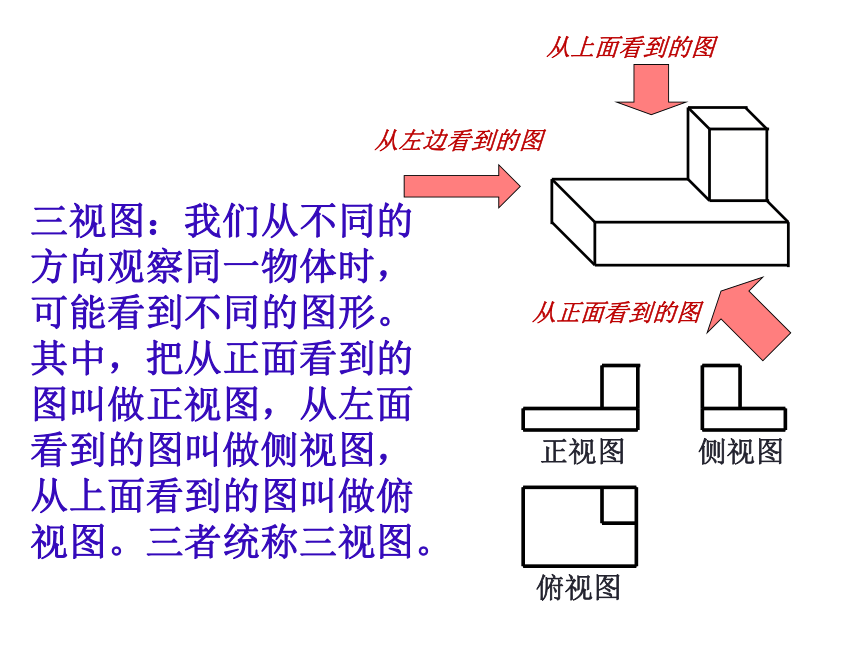
从正面看到的图
从左边看到的图
从上面看到的图
三视图:我们从不同的方向观察同一物体时,可能看到不同的图形。其中,把从正面看到的图叫做正视图,从左面看到的图叫做侧视图,从上面看到的图叫做俯视图。三者统称三视图。
正视图 侧视图
俯视图
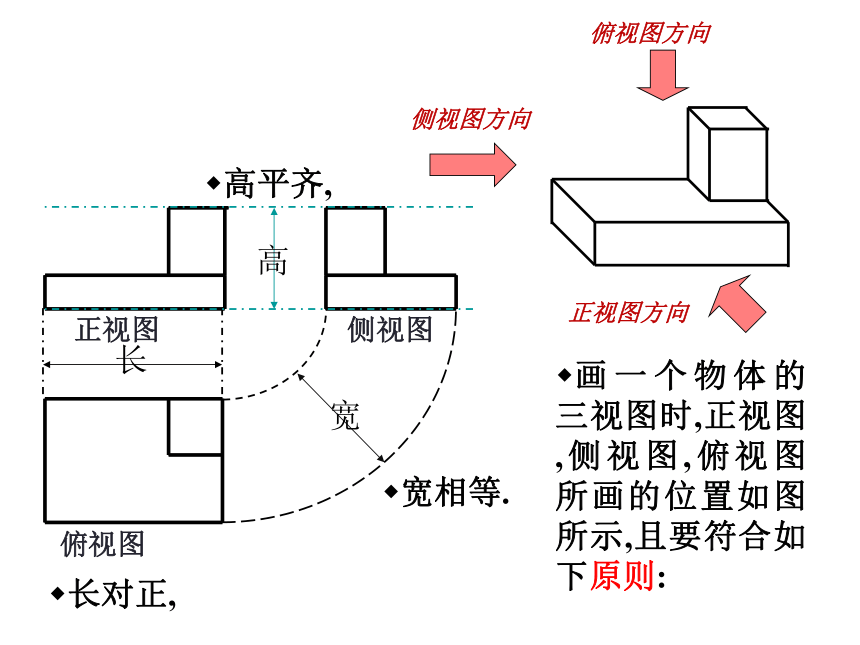
侧视图方向
俯视图方向
正视图方向
正视图 侧视图
俯视图
长
高
宽
画一个物体的三视图时,正视图,侧视图,俯视图所画的位置如图所示,且要符合如下原则:
长对正,
高平齐,
宽相等.
侧视图方向
俯视图方向
正视图方向
三视图的作图步骤
1.确定正视图方向
3.先画出能反映物体真实形状的一个视图(一般为正视图)
4.运用 1 原则画出其它视图
5.检查
2.布置视图
长对正、高平齐、宽相等
正视图 侧视图
俯视图
要求:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方。
下面各图中物体形状分另可以看成什么样的几何体
圆柱 圆锥 球
从正面,侧面,上面看这些几何体,它们的形状各是什么样的
正面看:长方体 等腰三角形 圆
侧面看:长方体 等腰三角形 圆
上面看: 圆 圆 圆
你能画出各物体的三视图吗
正视图
侧视图
俯视图
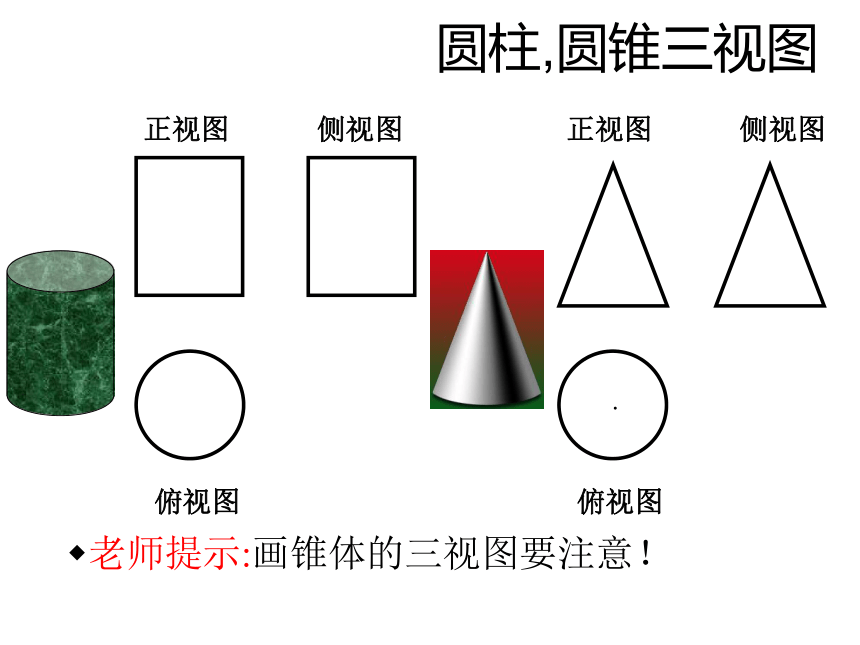
老师提示:画锥体的三视图要注意!
正视图
侧视图
俯视图
·
圆柱,圆锥三视图
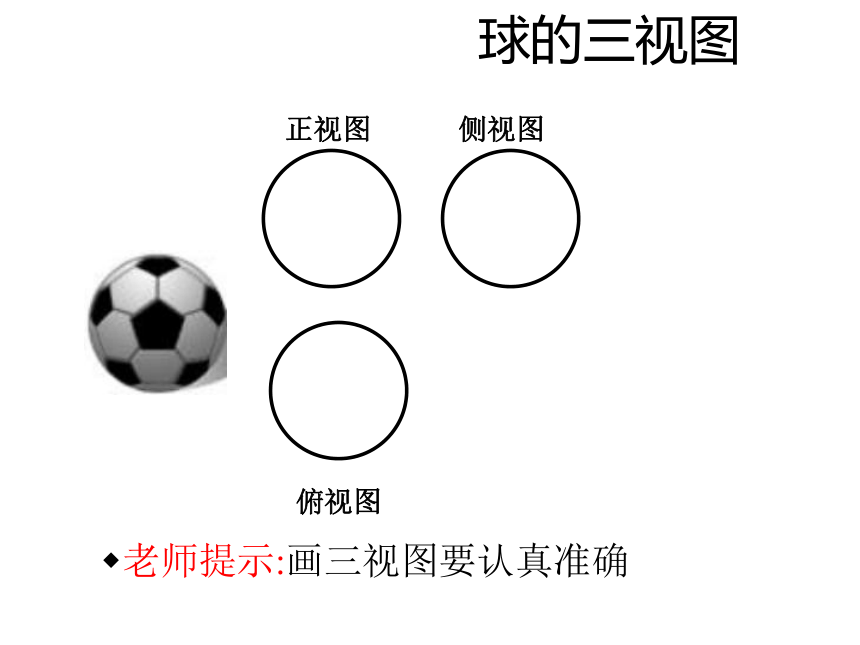
老师提示:画三视图要认真准确
正视图
侧视图
俯视图
球的三视图
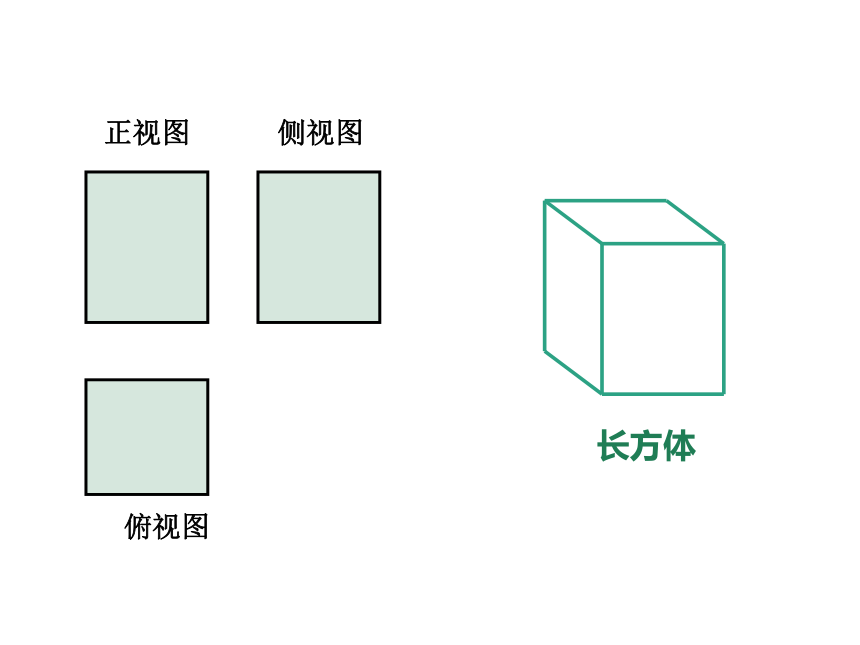
长方体
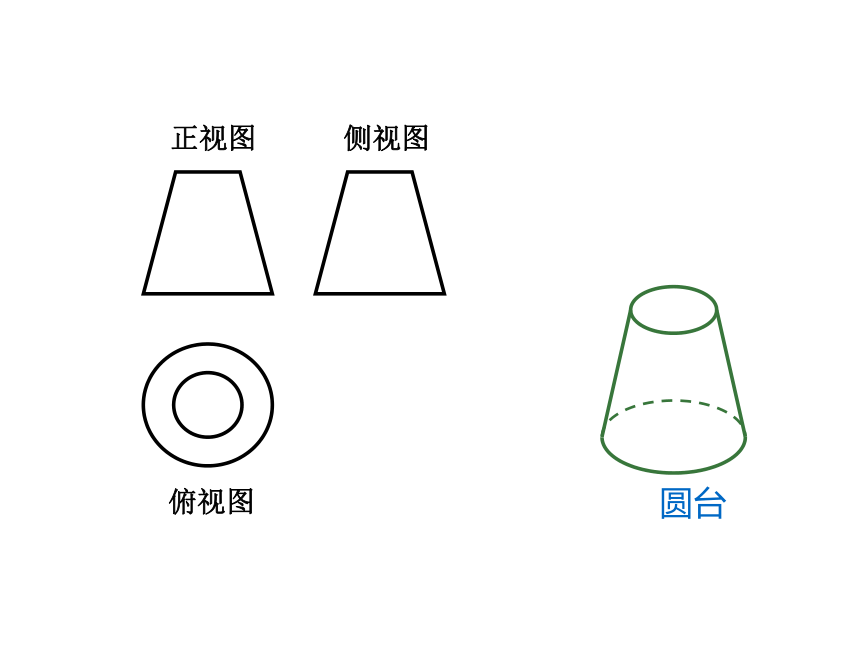
圆台
练习一: 画出下列基本几何体的三视图
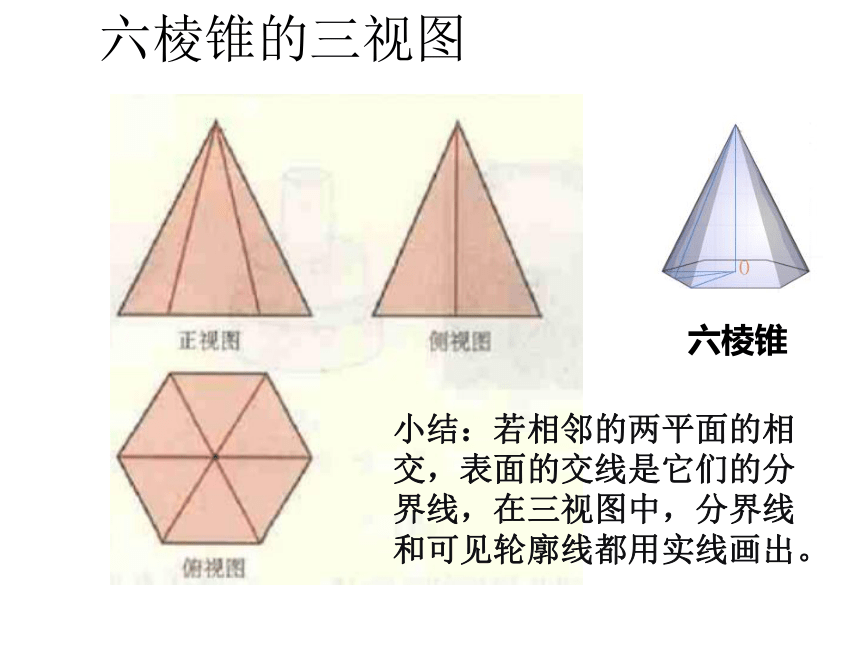
六棱锥
长方体
长方体
正视图
侧视图
俯视图
圆台
圆台
正视图
侧视图
俯视图
六棱锥
小结:若相邻的两平面的相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出。
六棱锥的三视图
例3:画出下面几何体的三视图。
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
注意:不可见的轮廓线,用虚线画出。
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
四棱锥
圆台
圆台
主
左
俯
体验三视图的作法
六棱柱
六棱柱
主
左
俯
体验三视图的作法
练一练:画出左图的三视图
先布局定作图基准,从俯视图开始画起,后画主、左视图。
请同学自己做
请同学自己做
先布局定作图基准,从俯视图开始画起,后画主、左视图。
Φ
Φ
如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,然后根据这三个图形制造出水管接头.
图2
图1
三通水管
练习: 根据三视图想像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
圆柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
马蹄形磁铁
前后看
从上向下看
左右看
例2. 图中几何体的主视图是( )
例3. 将图所示的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图形中的_____________(只填序号)
例4. 图5是由一些相同的小正方体构成的几何体的三视图。这些相同的小正方体的个数是( )
4个 B. 5个
C. 6个 D. 7个
例6. 一个画家有14个边长为1m的正方体,他在地面上把它们摆成如图8所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )
A. 19m2 B. 21m2
C. 33m2 D. 34m2
例7. 图10是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
2
3
5
2
4
A
B
C
D
小 结
三视图
正视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
从正面看到的图
从左边看到的图
从上面看到的图
三视图:我们从不同的方向观察同一物体时,可能看到不同的图形。其中,把从正面看到的图叫做正视图,从左面看到的图叫做侧视图,从上面看到的图叫做俯视图。三者统称三视图。
正视图 侧视图
俯视图
侧视图方向
俯视图方向
正视图方向
正视图 侧视图
俯视图
长
高
宽
画一个物体的三视图时,正视图,侧视图,俯视图所画的位置如图所示,且要符合如下原则:
长对正,
高平齐,
宽相等.
侧视图方向
俯视图方向
正视图方向
三视图的作图步骤
1.确定正视图方向
3.先画出能反映物体真实形状的一个视图(一般为正视图)
4.运用 1 原则画出其它视图
5.检查
2.布置视图
长对正、高平齐、宽相等
正视图 侧视图
俯视图
要求:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方。
下面各图中物体形状分另可以看成什么样的几何体
圆柱 圆锥 球
从正面,侧面,上面看这些几何体,它们的形状各是什么样的
正面看:长方体 等腰三角形 圆
侧面看:长方体 等腰三角形 圆
上面看: 圆 圆 圆
你能画出各物体的三视图吗
正视图
侧视图
俯视图
老师提示:画锥体的三视图要注意!
正视图
侧视图
俯视图
·
圆柱,圆锥三视图
老师提示:画三视图要认真准确
正视图
侧视图
俯视图
球的三视图
长方体
圆台
练习一: 画出下列基本几何体的三视图
六棱锥
长方体
长方体
正视图
侧视图
俯视图
圆台
圆台
正视图
侧视图
俯视图
六棱锥
小结:若相邻的两平面的相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出。
六棱锥的三视图
例3:画出下面几何体的三视图。
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
注意:不可见的轮廓线,用虚线画出。
简单组合体的三视图
正视图
侧视图
俯视图
简单组合体的三视图
四棱锥
圆台
圆台
主
左
俯
体验三视图的作法
六棱柱
六棱柱
主
左
俯
体验三视图的作法
练一练:画出左图的三视图
先布局定作图基准,从俯视图开始画起,后画主、左视图。
请同学自己做
请同学自己做
先布局定作图基准,从俯视图开始画起,后画主、左视图。
Φ
Φ
如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,然后根据这三个图形制造出水管接头.
图2
图1
三通水管
练习: 根据三视图想像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
圆柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
马蹄形磁铁
前后看
从上向下看
左右看
例2. 图中几何体的主视图是( )
例3. 将图所示的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图形中的_____________(只填序号)
例4. 图5是由一些相同的小正方体构成的几何体的三视图。这些相同的小正方体的个数是( )
4个 B. 5个
C. 6个 D. 7个
例6. 一个画家有14个边长为1m的正方体,他在地面上把它们摆成如图8所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )
A. 19m2 B. 21m2
C. 33m2 D. 34m2
例7. 图10是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
2
3
5
2
4
A
B
C
D
小 结
三视图
正视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
