北师大版数学八年级上册6.1 平均数课件(第2课时 21张)
文档属性
| 名称 | 北师大版数学八年级上册6.1 平均数课件(第2课时 21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 895.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:45:11 | ||
图片预览







文档简介
6.1 平均数(第2课时)
北师大版 数学 八年级 上册
一般地,对于n个数x1 ,x2 ,… ,xn ,我们把
( x1 + x2 + … + xn)
叫做这n个数的算术平均数,简称平均数,记作 x .
导入新知
1.什么是算术平均数?
2.什么是加权平均数?
一般地,如果在n个数中,x1出现f1次,x2出现f2次, ……,xk出现fk次(这时 f1+f2+……+fk=n ),那么这n个数的加权平均数为
2. 会用算术平均数和加权平均数解决一些实际问题.
1. 进一步理解加权平均数的意义,会求一组数据的加权平均数 .
素养目标
3. 通过解决实际问题,体会数学与社会生活的密切联系,增进对数学的理解和学好数学的信心.
服装统一
进退场有序
动作规范
动作整齐
一 班
9
8
9
8
二 班
10
9
7
8
三 班
8
9
8
9
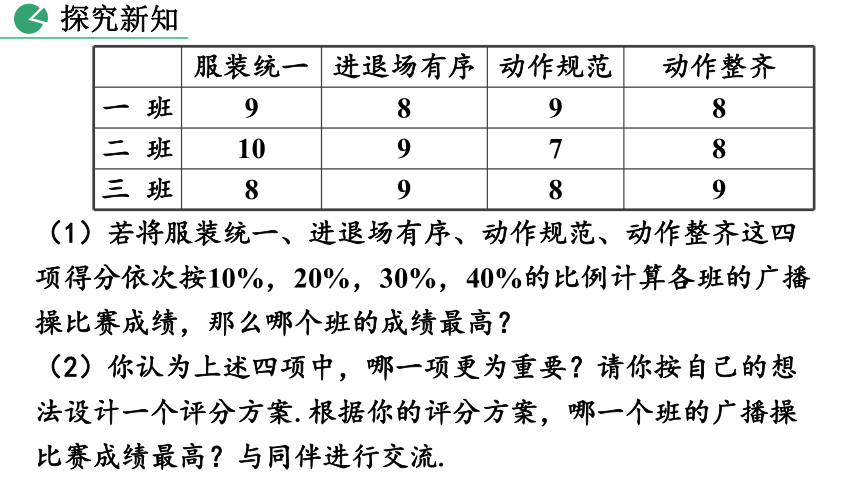
问题一 某学校进行广播操比赛,比赛打分包括以下几项:服装统一、进退场有序、动作规范、动作整齐(每项满分10分),其中三个班级的成绩分别如下:
探究新知
知识点
加权平均数的应用
探究新知
(1)若将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%,20%,30%,40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
(2)你认为上述四项中,哪一项更为重要?请你按自己的想法设计一个评分方案.根据你的评分方案,哪一个班的广播操比赛成绩最高?与同伴进行交流.
服装统一
进退场有序
动作规范
动作整齐
一 班
9
8
9
8
二 班
10
9
7
8
三 班
8
9
8
9
解:(1)一班的广播操成绩为:
9×10%+8×20%+9×30%+8×40%=8.4(分)
二班的广播操成绩为:
10×10%+9×20%+7×30%+8×40%=8.1(分)
三班的广播操成绩为:
8×10%+9×20%+8×30%+9×40%=8.6(分)
因此,三班的广播操成绩最高.
(2) 权有差异,得出的结果就会不同,也就是说权的差异对结果有影响.
探究新知
小颖家去年的饮食支出为3600元,教育支出为1200 元,其他支出为7200 元.小颖家今年的这三项支出依次比去年增长了9%,30%,6%,小颖家今年的总支出比去年增长的百分数是多少?
以下是小明和小亮的两种解法,谁做得对?说说你的理由.
小明:(9%+30%+6%)÷3=15%
小亮:(9%×3600+30%×1200+6%×7200)
÷(3600+1200+7200)=9.3%
探究新知
问题二
由于小颖家去年的饮食、教育和其他三项支出金额不等,因此,饮食、教育和其他三项支出的增长率“地位”不同,它们对总支出增长率的“影响”不同,不能简单地用算术平均数计算总支出的增长率,而应将这三项支出金额3600,1200,7200分别视为三项支出增长率的“权”,从而总支出的增长率为小亮的解法是对的.
日常生活中的许多“平均” 现象是“加权平均”.
探究新知
你能举出生活中加权平均数的实例吗?
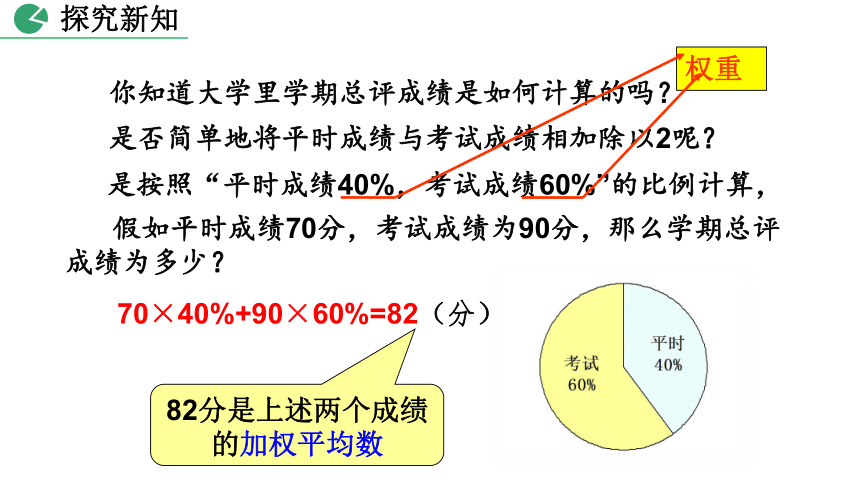
你知道大学里学期总评成绩是如何计算的吗?
是否简单地将平时成绩与考试成绩相加除以2呢?
是按照“平时成绩40%,考试成绩60%”的比例计算,
假如平时成绩70分,考试成绩为90分,那么学期总评成绩为多少?
70×40%+90×60%=82(分)
82分是上述两个成绩的加权平均数
权重
探究新知
解:(1)1小明的平均速度是(15×1+5×1)÷(1+1)=10(千米/时).
(2)小明的平均速度是(15×2+5×3)÷(2+3)=9(千米/时),
小明骑自行车的速度是15千米/时,步行的速度是5千米/时.
(1)如果小明先骑自行车1小时,然后又步行了1小时,那么他的平均速度是多少?
(2)如果小明先骑自行车2小时,然后步行了3小时,那么他的平均速度是多少?你能从权的角度来理解这样的平均速度吗?
巩固练习
小明骑自行车和步行的时间2小时,3小时分别是骑自行车和步行速度的权.
(2019?青岛)射击比赛中,某队员10次射击成绩如图所示,则该队员的平均成绩是_________环.
8.5
连接中考
1.面试时,某人的基本知识、表达能力、工作态度的得分分别是80分,70分,85分,若依次按 30%,30%,40% 的比例确定成绩,则这个人的面试成绩是多少?
解:80×30%+70×30%+85×40%=79(分)
答:这个人的面试成绩是79分.
课堂检测
基础巩固题
2.菲尔兹奖是数学领域的一项国际大奖,每四年颁发一次,从1936年到2010年共有53人获奖,获奖者获奖时的年龄分布如下,请计算获奖者的平均年龄.(精确到0.1岁)
课堂检测
基础巩固题
平均年龄=(28×1+29×3+31 × 4
+ 32 ×4+33 ×3 +34 × 3+35 ×5
+36 ×6+37 ×5+38 × 7+39 ×6+40
×5+45 ×1)÷(1+3 +4+4 + 3+
3 + 5 + 6+5+7+6+5+1)≈35.6(岁)
解:
答:获奖者的平均年龄约为35.6岁.
3.为了估计某矿区铁矿石的含铁量,抽取了15块矿石,测得它们的含铁量如下:(单位:%)
26
24
21
28
27
23
23
25
26
22
21
30
26
20
30
则样本的平均数是多少?
基础巩固题
课堂检测
解:
答:样本的平均数是24.8.
4.某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动表现占成绩的20%,体育理论测试占30%,体育技能测试占50%,小颖的上述三项成绩依次是92分、80分、84分,则小颖这学期的体育成绩是多少?
解:小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4(分).
答:小颖这学期的体育成绩是84.4分.
基础巩固题
课堂检测
分 数 段
组中值
人 数
40≤x<60
2
60≤x<80
8
80≤x<100
10
100≤x≤120
20
问班级平均分约是多少?
某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
课堂检测
能力提升题
答:班级平均分约是94分.
下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
课堂检测
拓广探索题
解:(1)因为点D,O,E在同一条直线上,所以∠DOE=180°,
所以60≤x<80所占百分比为180/360 ×100%=50%.
因为∠AOE=36°,
所以80≤x≤100所占百分比为36/360 ×100%=10%,
所以0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
故本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%=60(分)
课堂检测
拓广探索题
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
课堂检测
拓广探索题
加权平均数的应用
加权平均数的影响
加权平均数的实际应用
权的不同,导致结果不同,故权的差异对结果有影响
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
北师大版 数学 八年级 上册
一般地,对于n个数x1 ,x2 ,… ,xn ,我们把
( x1 + x2 + … + xn)
叫做这n个数的算术平均数,简称平均数,记作 x .
导入新知
1.什么是算术平均数?
2.什么是加权平均数?
一般地,如果在n个数中,x1出现f1次,x2出现f2次, ……,xk出现fk次(这时 f1+f2+……+fk=n ),那么这n个数的加权平均数为
2. 会用算术平均数和加权平均数解决一些实际问题.
1. 进一步理解加权平均数的意义,会求一组数据的加权平均数 .
素养目标
3. 通过解决实际问题,体会数学与社会生活的密切联系,增进对数学的理解和学好数学的信心.
服装统一
进退场有序
动作规范
动作整齐
一 班
9
8
9
8
二 班
10
9
7
8
三 班
8
9
8
9
问题一 某学校进行广播操比赛,比赛打分包括以下几项:服装统一、进退场有序、动作规范、动作整齐(每项满分10分),其中三个班级的成绩分别如下:
探究新知
知识点
加权平均数的应用
探究新知
(1)若将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%,20%,30%,40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
(2)你认为上述四项中,哪一项更为重要?请你按自己的想法设计一个评分方案.根据你的评分方案,哪一个班的广播操比赛成绩最高?与同伴进行交流.
服装统一
进退场有序
动作规范
动作整齐
一 班
9
8
9
8
二 班
10
9
7
8
三 班
8
9
8
9
解:(1)一班的广播操成绩为:
9×10%+8×20%+9×30%+8×40%=8.4(分)
二班的广播操成绩为:
10×10%+9×20%+7×30%+8×40%=8.1(分)
三班的广播操成绩为:
8×10%+9×20%+8×30%+9×40%=8.6(分)
因此,三班的广播操成绩最高.
(2) 权有差异,得出的结果就会不同,也就是说权的差异对结果有影响.
探究新知
小颖家去年的饮食支出为3600元,教育支出为1200 元,其他支出为7200 元.小颖家今年的这三项支出依次比去年增长了9%,30%,6%,小颖家今年的总支出比去年增长的百分数是多少?
以下是小明和小亮的两种解法,谁做得对?说说你的理由.
小明:(9%+30%+6%)÷3=15%
小亮:(9%×3600+30%×1200+6%×7200)
÷(3600+1200+7200)=9.3%
探究新知
问题二
由于小颖家去年的饮食、教育和其他三项支出金额不等,因此,饮食、教育和其他三项支出的增长率“地位”不同,它们对总支出增长率的“影响”不同,不能简单地用算术平均数计算总支出的增长率,而应将这三项支出金额3600,1200,7200分别视为三项支出增长率的“权”,从而总支出的增长率为小亮的解法是对的.
日常生活中的许多“平均” 现象是“加权平均”.
探究新知
你能举出生活中加权平均数的实例吗?
你知道大学里学期总评成绩是如何计算的吗?
是否简单地将平时成绩与考试成绩相加除以2呢?
是按照“平时成绩40%,考试成绩60%”的比例计算,
假如平时成绩70分,考试成绩为90分,那么学期总评成绩为多少?
70×40%+90×60%=82(分)
82分是上述两个成绩的加权平均数
权重
探究新知
解:(1)1小明的平均速度是(15×1+5×1)÷(1+1)=10(千米/时).
(2)小明的平均速度是(15×2+5×3)÷(2+3)=9(千米/时),
小明骑自行车的速度是15千米/时,步行的速度是5千米/时.
(1)如果小明先骑自行车1小时,然后又步行了1小时,那么他的平均速度是多少?
(2)如果小明先骑自行车2小时,然后步行了3小时,那么他的平均速度是多少?你能从权的角度来理解这样的平均速度吗?
巩固练习
小明骑自行车和步行的时间2小时,3小时分别是骑自行车和步行速度的权.
(2019?青岛)射击比赛中,某队员10次射击成绩如图所示,则该队员的平均成绩是_________环.
8.5
连接中考
1.面试时,某人的基本知识、表达能力、工作态度的得分分别是80分,70分,85分,若依次按 30%,30%,40% 的比例确定成绩,则这个人的面试成绩是多少?
解:80×30%+70×30%+85×40%=79(分)
答:这个人的面试成绩是79分.
课堂检测
基础巩固题
2.菲尔兹奖是数学领域的一项国际大奖,每四年颁发一次,从1936年到2010年共有53人获奖,获奖者获奖时的年龄分布如下,请计算获奖者的平均年龄.(精确到0.1岁)
课堂检测
基础巩固题
平均年龄=(28×1+29×3+31 × 4
+ 32 ×4+33 ×3 +34 × 3+35 ×5
+36 ×6+37 ×5+38 × 7+39 ×6+40
×5+45 ×1)÷(1+3 +4+4 + 3+
3 + 5 + 6+5+7+6+5+1)≈35.6(岁)
解:
答:获奖者的平均年龄约为35.6岁.
3.为了估计某矿区铁矿石的含铁量,抽取了15块矿石,测得它们的含铁量如下:(单位:%)
26
24
21
28
27
23
23
25
26
22
21
30
26
20
30
则样本的平均数是多少?
基础巩固题
课堂检测
解:
答:样本的平均数是24.8.
4.某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动表现占成绩的20%,体育理论测试占30%,体育技能测试占50%,小颖的上述三项成绩依次是92分、80分、84分,则小颖这学期的体育成绩是多少?
解:小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4(分).
答:小颖这学期的体育成绩是84.4分.
基础巩固题
课堂检测
分 数 段
组中值
人 数
40≤x<60
2
60≤x<80
8
80≤x<100
10
100≤x≤120
20
问班级平均分约是多少?
某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
课堂检测
能力提升题
答:班级平均分约是94分.
下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
课堂检测
拓广探索题
解:(1)因为点D,O,E在同一条直线上,所以∠DOE=180°,
所以60≤x<80所占百分比为180/360 ×100%=50%.
因为∠AOE=36°,
所以80≤x≤100所占百分比为36/360 ×100%=10%,
所以0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
故本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%=60(分)
课堂检测
拓广探索题
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
课堂检测
拓广探索题
加权平均数的应用
加权平均数的影响
加权平均数的实际应用
权的不同,导致结果不同,故权的差异对结果有影响
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
