人教版七年级上册数学课件:1.3.1有理数加法(共30张PPT)
文档属性
| 名称 | 人教版七年级上册数学课件:1.3.1有理数加法(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
第1章
有理数
有理数的加减(1)
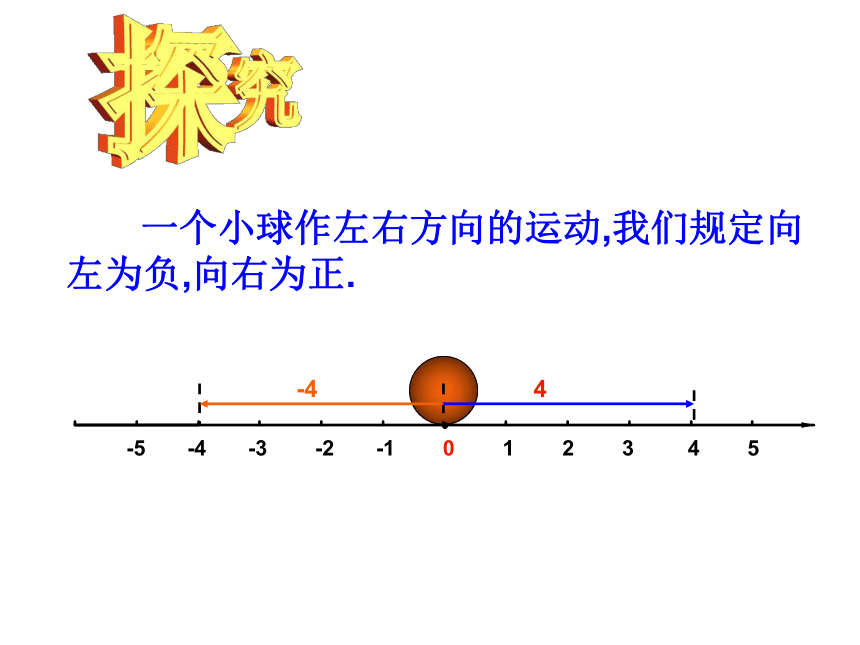
一个小球作左右方向的运动,我们规定向左为负,向右为正.
-5
-4
-3
-2
-1
0
1
2
3
4
5
4
-4
-1
-2
0
1
2
3
4
5
6
7
8
3
5
8
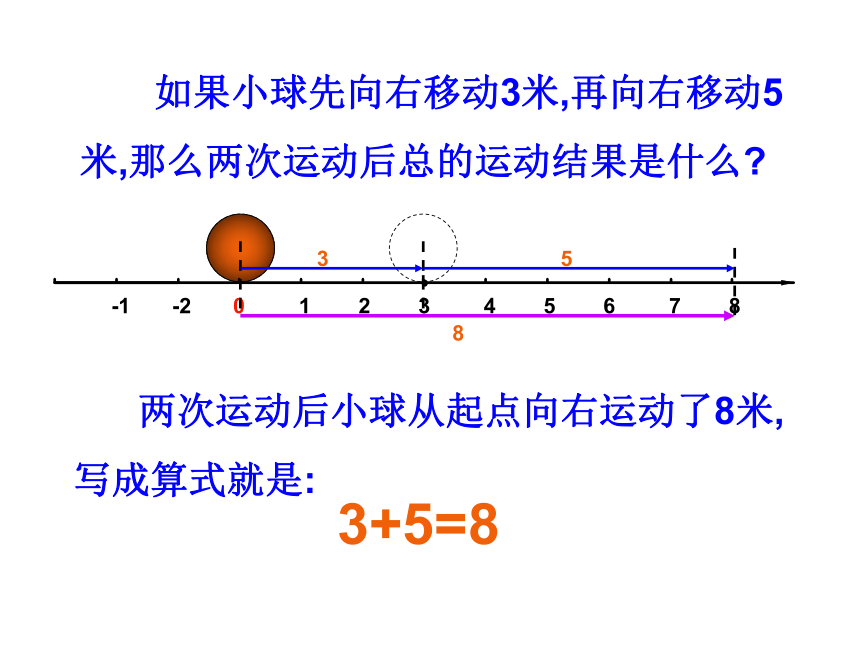
如果小球先向右移动3米,再向右移动5
米,那么两次运动后总的运动结果是什么?
3+5=8
两次运动后小球从起点向右运动了8米,
写成算式就是:
问题1.
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
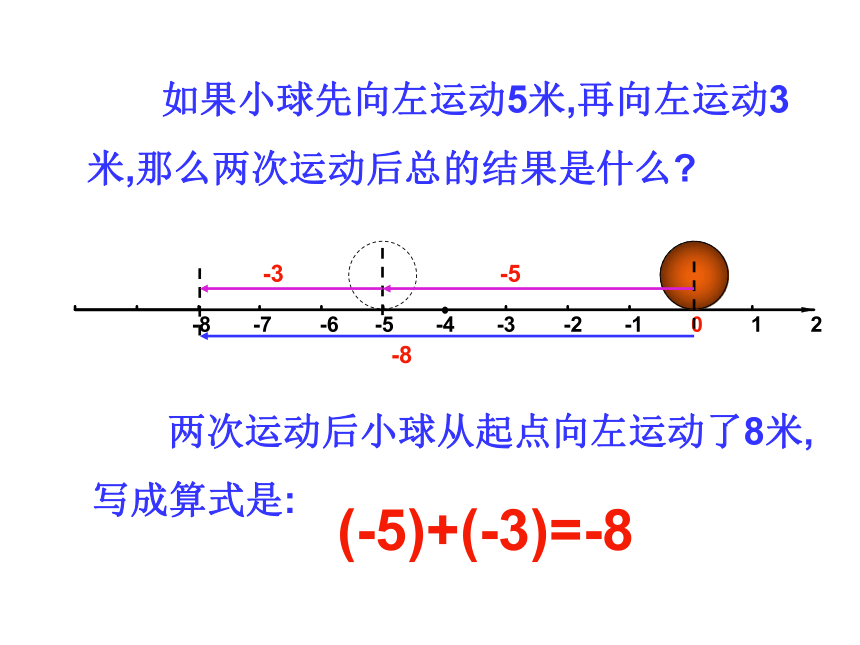
如果小球先向左运动5米,再向左运动3
米,那么两次运动后总的结果是什么?
问题2.
-5
-3
-8
两次运动后小球从起点向左运动了8米,
写成算式是:
(-5)+(-3)=-8
5
-3
2
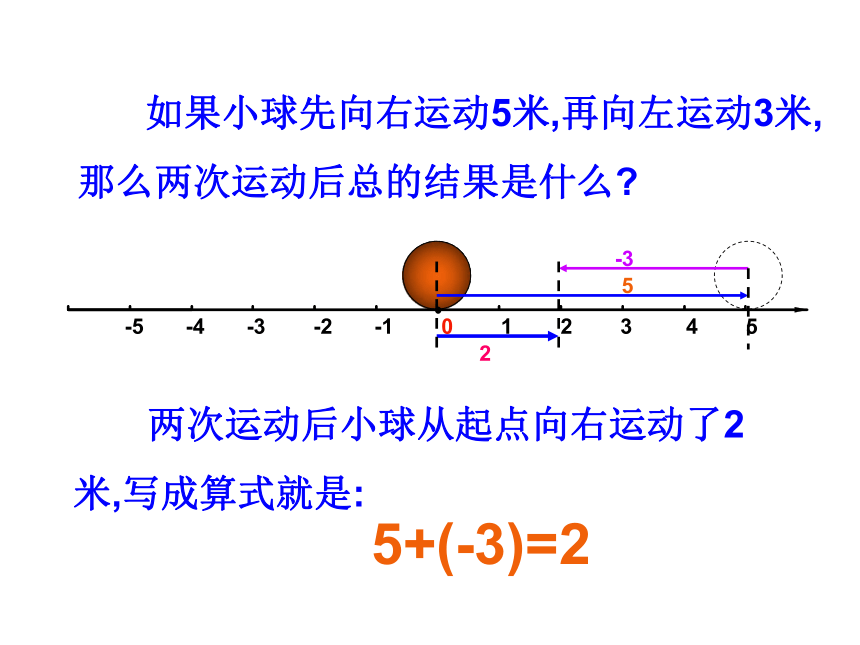
如果小球先向右运动5米,再向左运动3米,
那么两次运动后总的结果是什么?
两次运动后小球从起点向右运动了2
米,写成算式就是:
5+(-3)=2
-5
-4
-3
-2
-1
0
1
2
3
4
5
问题3.
-5
-4
-3
-2
-1
0
1
2
3
4
5
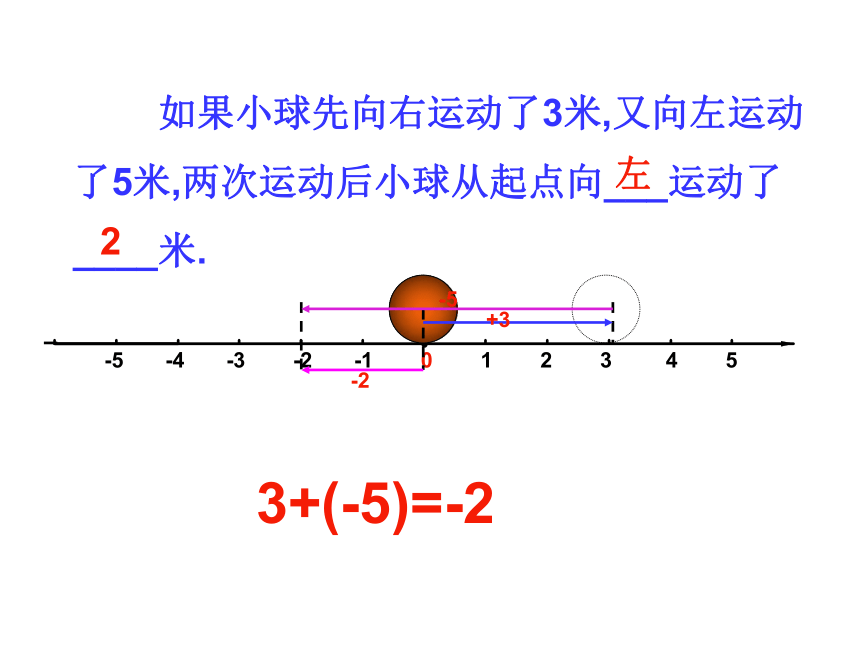
如果小球先向右运动了3米,又向左运动
了5米,两次运动后小球从起点向___运动了
____米.
+3
-5
-2
左
2
3+(-5)=-2
问题4.
-5
-4
-3
-2
-1
0
1
2
3
4
5
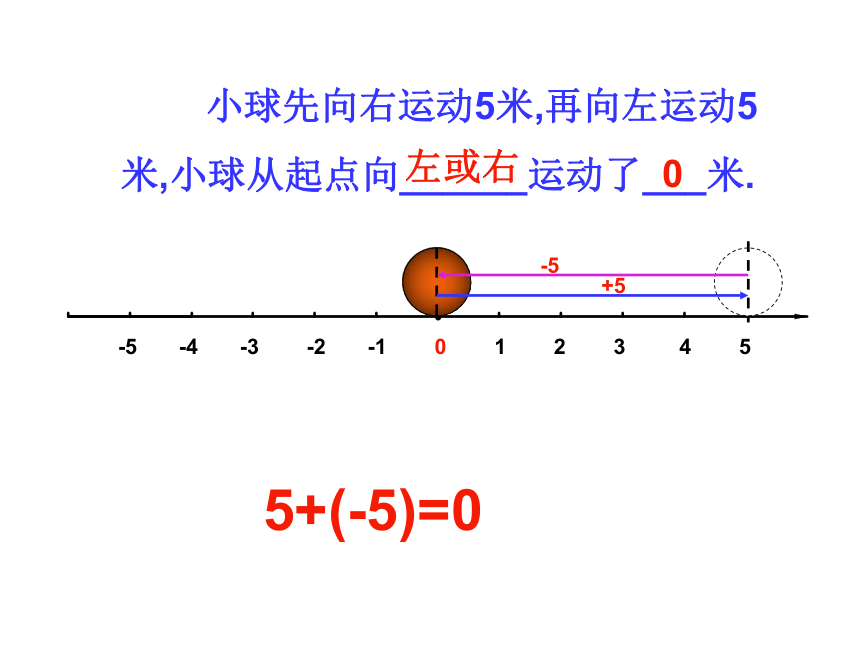
小球先向右运动5米,再向左运动5
米,小球从起点向______运动了___米.
5+(-5)=0
左或右
0
+5
-5
问题5.
-5
-4
-3
-2
-1
0
1
2
3
4
5
问题6.
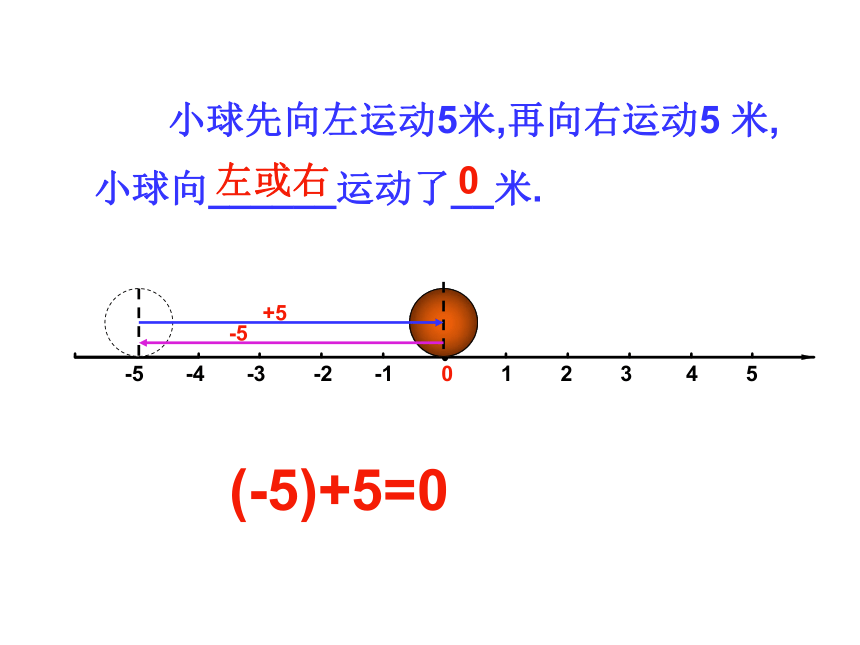
小球先向左运动5米,再向右运动5
米,
小球向______运动了__米.
-5
+5
左或右
0
(-5)+5=0
-5
-4
-3
-2
-1
0
1
2
3
4
5
问题7.
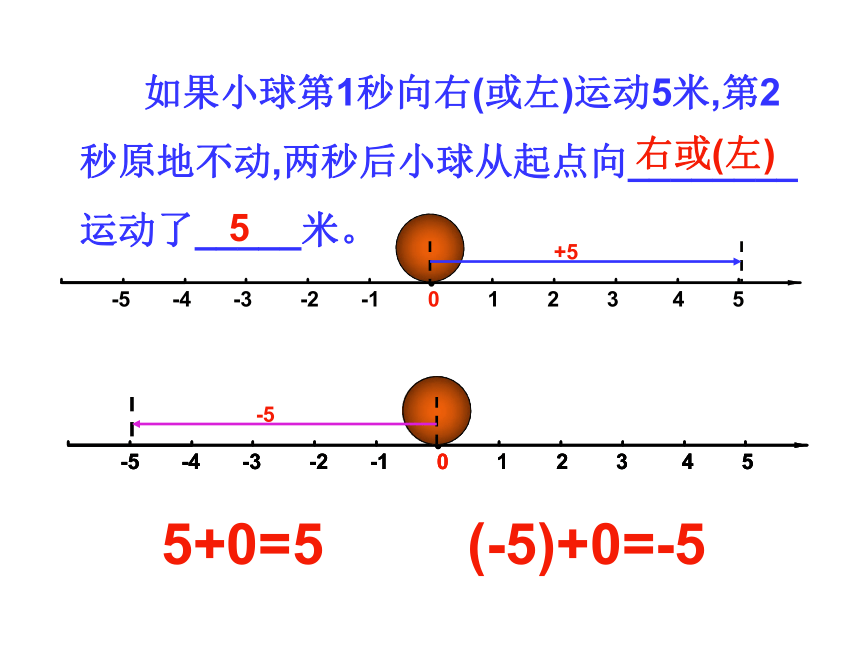
如果小球第1秒向右(或左)运动5米,第2
秒原地不动,两秒后小球从起点向________
运动了_____米。
-5
-4
-3
-2
-1
0
1
2
3
4
5
+5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
右或(左)
5
5+0=5
(-5)+0=-5
有理数加法的分类
5
+
3
=
8
(-5)+(-3)
=
-8
5
+
(-3)
=
2
3
+
(-5)
=
-2
5
+
(-5)
=
0
(-5)
+
5
=
0
5
+
0
=
5
(-5)
+
0
=
-5
同号两数相加
异号两数相加
一个数同零相加
归纳
有理数的加法法则:
⑴
同号两数相加,取相同的符号,并把绝
对值相加.
⑵
绝对值不相等的异号两数相加,取绝
对值较大的加数的符号,并用较大的绝对值减
去较小的绝对值.互为相反数的两个数相加和为0.
⑶
一个数同0相加,仍得这个数.
有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3.一个数同0相加,仍得这个数。
有理数加法运算的步骤:
确定和的符号
确定和的绝对值
同号
取相同的符号
两数绝对值之和
异号但绝对
值不等
取绝对值较大的
数的符号
较大的绝对值减
去较小的绝对值
异号且绝对
值相等
不是正数也不
是负数
0
一个数同0相加
取该数的符号
取该数的绝对值
分步
分类
(-4)
+
(-
8)
=
同号两数相加
(-9)
+
(+2)
=
异号两数相加
-
(
4
+
8
)
=
-
12
取相同符号
把绝对值相加
-
(
9
–
2
)
=
-
7
取绝对值较大的符号
用较大的绝对值减较小的绝对值
同号两数之和——这是名符其实的和,做加法。
异号两数之和——表面上叫“和”,其实是做减法。
试一试
加数
加数
和的组成
和
符号
绝对值
-15
5
17
6
-8
18
-8
-6
-10
5
-
+
+
-
-
15-5
17+6
18-8
8+6
10-5
-10
+23
+10
-14
-5
有理数加法运算的基本方法
一是辨别两个加数是同号还是异号,
二是确定和的符号,
三是判断应利用绝对值的和还是差进行计算.
有理数的加法运算涉及两个方面:
①符号的确定;②绝对值的计算
“一
辨”同异号;
“二定”和的符号;
“三求”和的绝对值(有加有减).
【例1】计算下列各题:
(1)180
+(-10);
(2)(-10)+(-1);
(3)5
+(-5);
(4)0+(-2).
解:(1)
180
+
(
-10)
(异号两数相加)
=
+
(180-10)
=
170;
(取绝对值较大的数的符号,
并用较大的绝对值减去较
小的绝对值)
(2)
(-10)
+
(-1)
(同号两数相加)
=
-(10+1)
=
-11;
(3)
5+(-5)
(互为相反数的两数相加)
=0;
⑷
0
+
(-2)
(一个数同0相加)
=-2.
(取相同的符号,并把
绝对值相加)
易错警示:
(1)两个负数相加时,结果容易忘记写“负号”,而只
把绝对值相加.
(2)异号两数相加时,对于和的符号判断错误,易把第
一个加数的符号作为和的符号或把绝对值相加作为
和的绝对值.
(3)书写的时候出现两个连着的符号,没有用括号分开.
如:2+-3,应写为2+(-3).
有理数的加法运算口诀:同号相加一边倒,异号相加“大”减“小”,符号跟着大的跑,绝对值相等“零”正好.
【注】“大”减“小”是指绝对值的大小.
有理数中的“和”与小学算术中
“和”的比较
和的符号
和与加数关系
算术中的“和”
不谈符号,通常是正数
比两个加数都大或相等
有理数中的“和”
可正、
可负、
可为零
可能比两个加数都大
可能比两个加数都小
可能大于其中一个而小于另一个加数
结果
类型
结论:在有理数运算中,算术中的某些结论不一定再成立。
练习1:口算下列各题,并说理由
(1)(+4)+(+7);
(2)(-4)+(-7);
(3)(+4)+(-7);
(4)(-4)+(+7)
;
(5)(+4)+(-4);
(6)(+9)+(-2);
(7)(-9)+(+2);
(8)(-9)+0
练一练
1、计算:
(1)、(+7)+(+6);
(2)、(-5)+(-9);
(4)、(-10.5)+(+21.5)
。
+
(3)、
;
2、计算:
(1)、(-7.5)+(+7.5);
(2)、(-3.5)+0。
练
习
【例2】
已知|a|=3,|b|=2,且a解:因为|a|=3,所以a=3或a=-3.
因为|b|=2,所以b=2或b=-2.
又因为a当a=-3,b=2时,a+b=(-3)+2=-1;
当a=-3,b=-2时,a+b=(-3)+(-2)=-5.
综上,a+b的值为-1或-5.
练习2:
1)计算:
(1)15+(-22);(2)(-0.9)+1.5;(3)2.7+(-3.5)
2)用“>”或“<”填空:
(1)如果a>0,b>0,那么a+b____0;
(2)
如果a<0,b<0,那么a+b____0;
(3)
如果a>0,b<0,|a|>|b|,那么a+b____0;
(4)
如果a<0,b>0,
|a|<|b|,那么a+b____0;
例4、在一次水下机器人测试中,机器人在海下时而上升,时而下降.机器人的初始位置在海平面下1
500米,下面是机器人在某段时间内的运动情况(把上升记为“+”,下降记为“-”,单位:米):-2
800,1
600.问:现在机器人处在什么位置?
【解】根据题意可得:上升为“+”,下降为“-”;
则现在机器人的位置距初始位置的距离是:
(-2
800)+1
600=-1
200(米).
故(-1
200)+(-1
500)=-2
700(米).
答:机器人现在处在海平面下2
700米处.
1、计算:
(1)、(-0.9)+(-2.7);
(2)、3.8+(-8.4);
(3)、(-0.5)+3;
(4)、3.29+1.78;
(5)、7+(-3.04);
(6)、(-2.9)+(-0.31);
(7)、(-9.18)+6.18;
(8)、(-0.78)+0。
作业布置
2、已知两数19,-27这两个数和的绝对值是_____,绝对值的和是______.
3、想一想,绝对值小于4的所有整数的和是_______。
4、某一条河第一天水位涨了9cm,第二天水下降了12cm,则最后水位涨了_____cm。
5、小李在东西大路上练习跑步,向东为正,向西为负,他跑的情况如下:5,-3,4,-6,-5,7,-4(单位:千米)最后停下时距离出发点多远?小明一共跑了多少千米?
一、有理数的加法法则
1、同号两数相加,取相同的符号,并把绝对值相加;
2、异号两数相加时:
(1)若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
(2)若绝对值相等,和为0,也就是相反数的和为0.
3、一个数与0的和仍得这个数.
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
小结:
课堂小结
有理数加法运算的步骤:
(1)根据有理数的加法法则确定和的符号;
+
-
0
(看另一个加数的符号)
+
-
(2)根据有理数的加法法则进行绝对值的加减运算。
第1章
有理数
有理数的加减(1)
一个小球作左右方向的运动,我们规定向左为负,向右为正.
-5
-4
-3
-2
-1
0
1
2
3
4
5
4
-4
-1
-2
0
1
2
3
4
5
6
7
8
3
5
8
如果小球先向右移动3米,再向右移动5
米,那么两次运动后总的运动结果是什么?
3+5=8
两次运动后小球从起点向右运动了8米,
写成算式就是:
问题1.
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
如果小球先向左运动5米,再向左运动3
米,那么两次运动后总的结果是什么?
问题2.
-5
-3
-8
两次运动后小球从起点向左运动了8米,
写成算式是:
(-5)+(-3)=-8
5
-3
2
如果小球先向右运动5米,再向左运动3米,
那么两次运动后总的结果是什么?
两次运动后小球从起点向右运动了2
米,写成算式就是:
5+(-3)=2
-5
-4
-3
-2
-1
0
1
2
3
4
5
问题3.
-5
-4
-3
-2
-1
0
1
2
3
4
5
如果小球先向右运动了3米,又向左运动
了5米,两次运动后小球从起点向___运动了
____米.
+3
-5
-2
左
2
3+(-5)=-2
问题4.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小球先向右运动5米,再向左运动5
米,小球从起点向______运动了___米.
5+(-5)=0
左或右
0
+5
-5
问题5.
-5
-4
-3
-2
-1
0
1
2
3
4
5
问题6.
小球先向左运动5米,再向右运动5
米,
小球向______运动了__米.
-5
+5
左或右
0
(-5)+5=0
-5
-4
-3
-2
-1
0
1
2
3
4
5
问题7.
如果小球第1秒向右(或左)运动5米,第2
秒原地不动,两秒后小球从起点向________
运动了_____米。
-5
-4
-3
-2
-1
0
1
2
3
4
5
+5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
右或(左)
5
5+0=5
(-5)+0=-5
有理数加法的分类
5
+
3
=
8
(-5)+(-3)
=
-8
5
+
(-3)
=
2
3
+
(-5)
=
-2
5
+
(-5)
=
0
(-5)
+
5
=
0
5
+
0
=
5
(-5)
+
0
=
-5
同号两数相加
异号两数相加
一个数同零相加
归纳
有理数的加法法则:
⑴
同号两数相加,取相同的符号,并把绝
对值相加.
⑵
绝对值不相等的异号两数相加,取绝
对值较大的加数的符号,并用较大的绝对值减
去较小的绝对值.互为相反数的两个数相加和为0.
⑶
一个数同0相加,仍得这个数.
有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3.一个数同0相加,仍得这个数。
有理数加法运算的步骤:
确定和的符号
确定和的绝对值
同号
取相同的符号
两数绝对值之和
异号但绝对
值不等
取绝对值较大的
数的符号
较大的绝对值减
去较小的绝对值
异号且绝对
值相等
不是正数也不
是负数
0
一个数同0相加
取该数的符号
取该数的绝对值
分步
分类
(-4)
+
(-
8)
=
同号两数相加
(-9)
+
(+2)
=
异号两数相加
-
(
4
+
8
)
=
-
12
取相同符号
把绝对值相加
-
(
9
–
2
)
=
-
7
取绝对值较大的符号
用较大的绝对值减较小的绝对值
同号两数之和——这是名符其实的和,做加法。
异号两数之和——表面上叫“和”,其实是做减法。
试一试
加数
加数
和的组成
和
符号
绝对值
-15
5
17
6
-8
18
-8
-6
-10
5
-
+
+
-
-
15-5
17+6
18-8
8+6
10-5
-10
+23
+10
-14
-5
有理数加法运算的基本方法
一是辨别两个加数是同号还是异号,
二是确定和的符号,
三是判断应利用绝对值的和还是差进行计算.
有理数的加法运算涉及两个方面:
①符号的确定;②绝对值的计算
“一
辨”同异号;
“二定”和的符号;
“三求”和的绝对值(有加有减).
【例1】计算下列各题:
(1)180
+(-10);
(2)(-10)+(-1);
(3)5
+(-5);
(4)0+(-2).
解:(1)
180
+
(
-10)
(异号两数相加)
=
+
(180-10)
=
170;
(取绝对值较大的数的符号,
并用较大的绝对值减去较
小的绝对值)
(2)
(-10)
+
(-1)
(同号两数相加)
=
-(10+1)
=
-11;
(3)
5+(-5)
(互为相反数的两数相加)
=0;
⑷
0
+
(-2)
(一个数同0相加)
=-2.
(取相同的符号,并把
绝对值相加)
易错警示:
(1)两个负数相加时,结果容易忘记写“负号”,而只
把绝对值相加.
(2)异号两数相加时,对于和的符号判断错误,易把第
一个加数的符号作为和的符号或把绝对值相加作为
和的绝对值.
(3)书写的时候出现两个连着的符号,没有用括号分开.
如:2+-3,应写为2+(-3).
有理数的加法运算口诀:同号相加一边倒,异号相加“大”减“小”,符号跟着大的跑,绝对值相等“零”正好.
【注】“大”减“小”是指绝对值的大小.
有理数中的“和”与小学算术中
“和”的比较
和的符号
和与加数关系
算术中的“和”
不谈符号,通常是正数
比两个加数都大或相等
有理数中的“和”
可正、
可负、
可为零
可能比两个加数都大
可能比两个加数都小
可能大于其中一个而小于另一个加数
结果
类型
结论:在有理数运算中,算术中的某些结论不一定再成立。
练习1:口算下列各题,并说理由
(1)(+4)+(+7);
(2)(-4)+(-7);
(3)(+4)+(-7);
(4)(-4)+(+7)
;
(5)(+4)+(-4);
(6)(+9)+(-2);
(7)(-9)+(+2);
(8)(-9)+0
练一练
1、计算:
(1)、(+7)+(+6);
(2)、(-5)+(-9);
(4)、(-10.5)+(+21.5)
。
+
(3)、
;
2、计算:
(1)、(-7.5)+(+7.5);
(2)、(-3.5)+0。
练
习
【例2】
已知|a|=3,|b|=2,且a
因为|b|=2,所以b=2或b=-2.
又因为a
当a=-3,b=-2时,a+b=(-3)+(-2)=-5.
综上,a+b的值为-1或-5.
练习2:
1)计算:
(1)15+(-22);(2)(-0.9)+1.5;(3)2.7+(-3.5)
2)用“>”或“<”填空:
(1)如果a>0,b>0,那么a+b____0;
(2)
如果a<0,b<0,那么a+b____0;
(3)
如果a>0,b<0,|a|>|b|,那么a+b____0;
(4)
如果a<0,b>0,
|a|<|b|,那么a+b____0;
例4、在一次水下机器人测试中,机器人在海下时而上升,时而下降.机器人的初始位置在海平面下1
500米,下面是机器人在某段时间内的运动情况(把上升记为“+”,下降记为“-”,单位:米):-2
800,1
600.问:现在机器人处在什么位置?
【解】根据题意可得:上升为“+”,下降为“-”;
则现在机器人的位置距初始位置的距离是:
(-2
800)+1
600=-1
200(米).
故(-1
200)+(-1
500)=-2
700(米).
答:机器人现在处在海平面下2
700米处.
1、计算:
(1)、(-0.9)+(-2.7);
(2)、3.8+(-8.4);
(3)、(-0.5)+3;
(4)、3.29+1.78;
(5)、7+(-3.04);
(6)、(-2.9)+(-0.31);
(7)、(-9.18)+6.18;
(8)、(-0.78)+0。
作业布置
2、已知两数19,-27这两个数和的绝对值是_____,绝对值的和是______.
3、想一想,绝对值小于4的所有整数的和是_______。
4、某一条河第一天水位涨了9cm,第二天水下降了12cm,则最后水位涨了_____cm。
5、小李在东西大路上练习跑步,向东为正,向西为负,他跑的情况如下:5,-3,4,-6,-5,7,-4(单位:千米)最后停下时距离出发点多远?小明一共跑了多少千米?
一、有理数的加法法则
1、同号两数相加,取相同的符号,并把绝对值相加;
2、异号两数相加时:
(1)若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
(2)若绝对值相等,和为0,也就是相反数的和为0.
3、一个数与0的和仍得这个数.
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
小结:
课堂小结
有理数加法运算的步骤:
(1)根据有理数的加法法则确定和的符号;
+
-
0
(看另一个加数的符号)
+
-
(2)根据有理数的加法法则进行绝对值的加减运算。
