北师大版七年级数学上册:2.1 有理数 课件(共26张PPT)
文档属性
| 名称 | 北师大版七年级数学上册:2.1 有理数 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-06 21:44:40 | ||
图片预览






文档简介
(共26张PPT)
2.1
有理数
第二章
有理数及其运算
北师版七年级数学上册
1.
数的起源
古代猎人打了一只老鹰,用数如何表示一只老鹰——有了整数.
新课导入
二人分一只西瓜,用数如何表示半只西瓜——有了分数.
新课导入
货币购物,用数如何表示2元3角4分——有了小数.
新课导入
2.
负数来源于生活
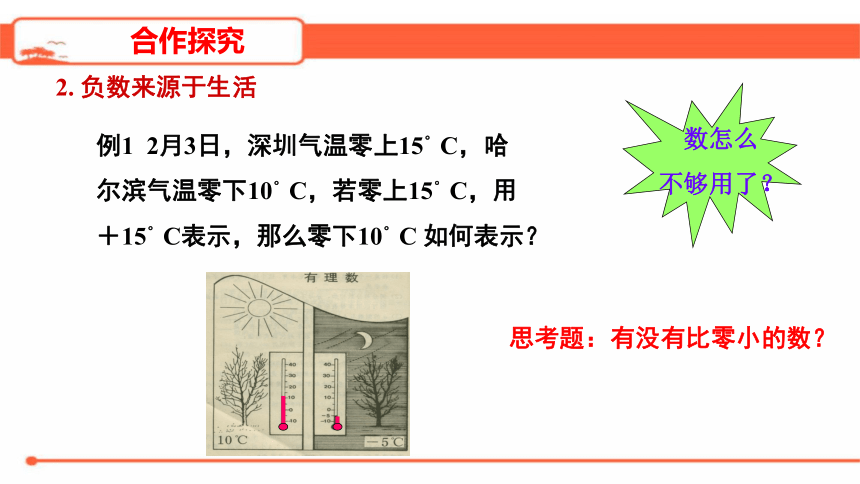
例1
2月3日,深圳气温零上15°C,哈尔滨气温零下10°C,若零上15°C,用+15°C表示,那么零下10°C
如何表示?
数怎么
不够用了?
思考题:有没有比零小的数?
合作探究
例2
我国有一座世界最高峰——珠穆朗玛峰,高度比海平面高
8848
米,在新疆境内,还有一个吐鲁番盆地,高度比海平面低
155
米,若海平面的高度为零度,则它们的高度分别如何表示?
-155
海平面
吐鲁番盆地
珠穆朗玛峰
8848
合作探究
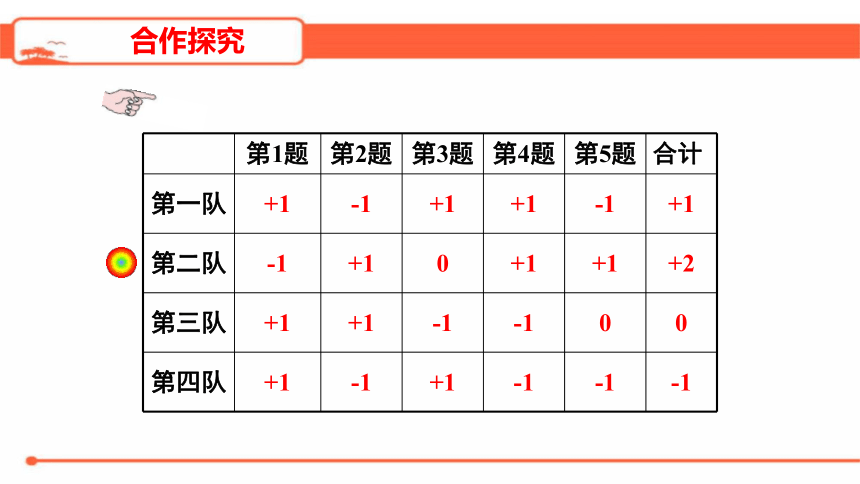
加1分
扣1分
得0分
第1题
第2题
第3题
第4题
第5题
第一队
第二队
第三队
第四队
合作探究
第1题
第2题
第3题
第4题
第5题
合计
第一队
+1
-1
+1
+1
-1
+1
第二队
-1
+1
0
+1
+1
+2
第三队
+1
+1
-1
-1
0
0
第四队
+1
-1
+1
-1
-1
-1
合作探究
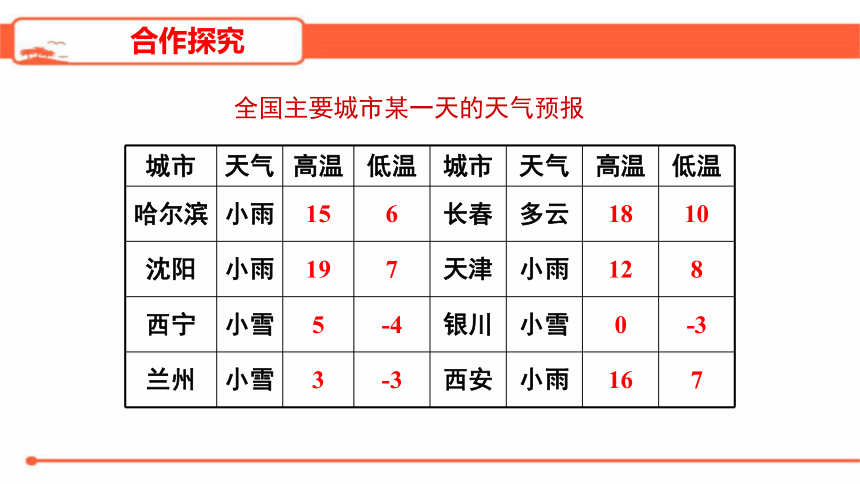
全国主要城市某一天的天气预报
城市
天气
高温
低温
城市
天气
高温
低温
哈尔滨
小雨
15
6
长春
多云
18
10
沈阳
小雨
19
7
天津
小雨
12
8
西宁
小雪
5
-4
银川
小雪
0
-3
兰州
小雪
3
-3
西安
小雨
16
7
合作探究
3.
正、负数的概念
像+5,+1.2,+
等大于零的数,叫做正数.
它们都比零大.
像-5,-1.5,
-
等在正数前面加上“
-
”
号的数叫做负数,
它们都比零小.
“
0
”
既不是正数,也不是负数.
“
0
”
具有中性特征.
合作探究
4.
用正负数表示生活中意义相反的量
议一议:举一些生活中象增加与减少,
升高与降低,
盈利与亏损,
零上与零下,收入与支出等实例.
合作探究
财富全球强中的主要零售企业
排名
公司
年收入
利润
雇员人数/人
2
沃尔玛
166809.0
5377.0
1140000
46
麦德龙
46663.6
295.1
171440
66
家乐福
39855.7
805.6
297290
111
特斯科
30351.9
1088.4
134896
153
大荣
25320.1
-195.2
47953
184
佳士客
22451.3
-25.2
34375
单位:百万美元
合作探究
1.生活中到处都存在相反意义的量.
2.在相反意义的量中,我们把其中一个意义的量规定为正,
那么另一个量就是负.
要点精析:
(1)相反意义的量是指意义相反的两个量,相反意义
的量是成对出现的.
(2)判断相反意义的量的标准:①两个同类量;②意义相反.
(3)具有相反意义的量的正负性是相对的,且是可以互换的.
归纳总结
5.
有理数的分类
……
负分数
整数
分数
有理数
1,2,3
0
-1,-2,-3
……正整数
……零
……负整数
……
正分数
合作探究
要点精析:
(1)正数的实质就是大于0的任何数,它可以含“+”,也可以不含“+”;
(2)负数就是在正数前面加上“-”的数,每一个正
数都对应一个负数;
(3)判断一个数是正、负数的方法:①不为零;②含
“+”“-”的情况
(无“+”
“-”视同含“+”),两者必须同时看.
归纳总结
数的特征及种类:
(1)数有带符号(+、-)的数和不带符号的数两
种呈现形式;
(2)数包括正数、0、负数三种情况.
拓展:符号“+”
“-”的含义:
(1)作为运算符号是加减号;
(2)作为数的性质是正负号.
归纳总结
例1
下列各数中,哪些是正数?哪些是负数?
+0.005,-100,
0.333…,-4,5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
警示:0既不是正数,也不是负数.
例题精析
解题关键点
特征
结论
看符号
数(0除外)前面带“+”
或无符号
正数
数(0除外)前面带
“-”的数
负数
例题精析
例2
(1)某人转动转盘,如果用+5圈表示沿逆时针方
向转了
5圈,那么沿顺时针方向转了
12圈怎
样表示?
(2)在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02
g记作+0.02
g,
那么-
0.03
g表示什么?
(3)某大米包装袋上标注着“净含
量:10
kg
±
150
g”,这里的
“10
kg
±150
g”表示什么?
例题精析
解:(1)沿顺时针方向转了
12圈记作-12圈;
(2)-0.03
g表示乒乓球的质量低于标准质量0.03
g;
(3)每袋大米的标准质量应为10
kg,但实际每袋大米
可能有150
g的误差,即每袋大米的净含量最多
是10
kg+150
g,最少是10
kg-150
g.
例题精析
例3
把下列各数分别填入相应的集合里:-2,0,
-0.314,25%,11,
非负有理数集合:{
…};
整数集合:{
…};
自然数集合:{
…};
分数集合:{
…};
非正整数集合:{
…}.
导引:要严格按照各类数的概念进行填写,非负有
理数包含正有理数和0;非正整数包含负整数和0.
例题精析
要点精析:
(1)非负有理数一定是有理数,它包含正有理数和0,
不要误认为是除负有理数以外的任何数;
(2)非正整数一定是整数;
(3)找各类数时,要时刻考虑它是否包括“0”.
例题精析
2
下列各组数,都是正数或都是负数的是( )
A.8,4,-2
B.2,5.4,
C.-6,0.5,0
D.0,6,9
1
四个数-3.14,0,1,2中为负数的是( )
A.-3.14
B.0
C.1
D.2
A
B
3
如果水位升高6
m时水位变化记作+6m,那么水位下降6
m时水位变化记作( )
A.-3
m
B.3
m
C.6
m
D.-6
m
D
课堂精练
4
如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
C
课堂精练
5
将下列各数填入如图所示的相应的圈内.
正数集合
整数集合
负数集合
课堂精练
判断具有相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必
须是同类量.
(2)单位一致:两个具有相反意义的量在数量上可以不
相等,但单位必须一致.
注意:用正数、负数表示相反意义的量时,哪种意
义为正没有硬性规定,并不是一成不变的.
课堂小结
2.1
有理数
第二章
有理数及其运算
北师版七年级数学上册
1.
数的起源
古代猎人打了一只老鹰,用数如何表示一只老鹰——有了整数.
新课导入
二人分一只西瓜,用数如何表示半只西瓜——有了分数.
新课导入
货币购物,用数如何表示2元3角4分——有了小数.
新课导入
2.
负数来源于生活
例1
2月3日,深圳气温零上15°C,哈尔滨气温零下10°C,若零上15°C,用+15°C表示,那么零下10°C
如何表示?
数怎么
不够用了?
思考题:有没有比零小的数?
合作探究
例2
我国有一座世界最高峰——珠穆朗玛峰,高度比海平面高
8848
米,在新疆境内,还有一个吐鲁番盆地,高度比海平面低
155
米,若海平面的高度为零度,则它们的高度分别如何表示?
-155
海平面
吐鲁番盆地
珠穆朗玛峰
8848
合作探究
加1分
扣1分
得0分
第1题
第2题
第3题
第4题
第5题
第一队
第二队
第三队
第四队
合作探究
第1题
第2题
第3题
第4题
第5题
合计
第一队
+1
-1
+1
+1
-1
+1
第二队
-1
+1
0
+1
+1
+2
第三队
+1
+1
-1
-1
0
0
第四队
+1
-1
+1
-1
-1
-1
合作探究
全国主要城市某一天的天气预报
城市
天气
高温
低温
城市
天气
高温
低温
哈尔滨
小雨
15
6
长春
多云
18
10
沈阳
小雨
19
7
天津
小雨
12
8
西宁
小雪
5
-4
银川
小雪
0
-3
兰州
小雪
3
-3
西安
小雨
16
7
合作探究
3.
正、负数的概念
像+5,+1.2,+
等大于零的数,叫做正数.
它们都比零大.
像-5,-1.5,
-
等在正数前面加上“
-
”
号的数叫做负数,
它们都比零小.
“
0
”
既不是正数,也不是负数.
“
0
”
具有中性特征.
合作探究
4.
用正负数表示生活中意义相反的量
议一议:举一些生活中象增加与减少,
升高与降低,
盈利与亏损,
零上与零下,收入与支出等实例.
合作探究
财富全球强中的主要零售企业
排名
公司
年收入
利润
雇员人数/人
2
沃尔玛
166809.0
5377.0
1140000
46
麦德龙
46663.6
295.1
171440
66
家乐福
39855.7
805.6
297290
111
特斯科
30351.9
1088.4
134896
153
大荣
25320.1
-195.2
47953
184
佳士客
22451.3
-25.2
34375
单位:百万美元
合作探究
1.生活中到处都存在相反意义的量.
2.在相反意义的量中,我们把其中一个意义的量规定为正,
那么另一个量就是负.
要点精析:
(1)相反意义的量是指意义相反的两个量,相反意义
的量是成对出现的.
(2)判断相反意义的量的标准:①两个同类量;②意义相反.
(3)具有相反意义的量的正负性是相对的,且是可以互换的.
归纳总结
5.
有理数的分类
……
负分数
整数
分数
有理数
1,2,3
0
-1,-2,-3
……正整数
……零
……负整数
……
正分数
合作探究
要点精析:
(1)正数的实质就是大于0的任何数,它可以含“+”,也可以不含“+”;
(2)负数就是在正数前面加上“-”的数,每一个正
数都对应一个负数;
(3)判断一个数是正、负数的方法:①不为零;②含
“+”“-”的情况
(无“+”
“-”视同含“+”),两者必须同时看.
归纳总结
数的特征及种类:
(1)数有带符号(+、-)的数和不带符号的数两
种呈现形式;
(2)数包括正数、0、负数三种情况.
拓展:符号“+”
“-”的含义:
(1)作为运算符号是加减号;
(2)作为数的性质是正负号.
归纳总结
例1
下列各数中,哪些是正数?哪些是负数?
+0.005,-100,
0.333…,-4,5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
警示:0既不是正数,也不是负数.
例题精析
解题关键点
特征
结论
看符号
数(0除外)前面带“+”
或无符号
正数
数(0除外)前面带
“-”的数
负数
例题精析
例2
(1)某人转动转盘,如果用+5圈表示沿逆时针方
向转了
5圈,那么沿顺时针方向转了
12圈怎
样表示?
(2)在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02
g记作+0.02
g,
那么-
0.03
g表示什么?
(3)某大米包装袋上标注着“净含
量:10
kg
±
150
g”,这里的
“10
kg
±150
g”表示什么?
例题精析
解:(1)沿顺时针方向转了
12圈记作-12圈;
(2)-0.03
g表示乒乓球的质量低于标准质量0.03
g;
(3)每袋大米的标准质量应为10
kg,但实际每袋大米
可能有150
g的误差,即每袋大米的净含量最多
是10
kg+150
g,最少是10
kg-150
g.
例题精析
例3
把下列各数分别填入相应的集合里:-2,0,
-0.314,25%,11,
非负有理数集合:{
…};
整数集合:{
…};
自然数集合:{
…};
分数集合:{
…};
非正整数集合:{
…}.
导引:要严格按照各类数的概念进行填写,非负有
理数包含正有理数和0;非正整数包含负整数和0.
例题精析
要点精析:
(1)非负有理数一定是有理数,它包含正有理数和0,
不要误认为是除负有理数以外的任何数;
(2)非正整数一定是整数;
(3)找各类数时,要时刻考虑它是否包括“0”.
例题精析
2
下列各组数,都是正数或都是负数的是( )
A.8,4,-2
B.2,5.4,
C.-6,0.5,0
D.0,6,9
1
四个数-3.14,0,1,2中为负数的是( )
A.-3.14
B.0
C.1
D.2
A
B
3
如果水位升高6
m时水位变化记作+6m,那么水位下降6
m时水位变化记作( )
A.-3
m
B.3
m
C.6
m
D.-6
m
D
课堂精练
4
如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
C
课堂精练
5
将下列各数填入如图所示的相应的圈内.
正数集合
整数集合
负数集合
课堂精练
判断具有相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必
须是同类量.
(2)单位一致:两个具有相反意义的量在数量上可以不
相等,但单位必须一致.
注意:用正数、负数表示相反意义的量时,哪种意
义为正没有硬性规定,并不是一成不变的.
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
