五年级上册数学课件-玩转《因数与倍数》青岛版 (共22张PPT)
文档属性
| 名称 | 五年级上册数学课件-玩转《因数与倍数》青岛版 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 870.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 06:12:01 | ||
图片预览







文档简介
(共22张PPT)
学号游戏
玩转《因数与倍数》
1
闻“数”起舞
游戏:闻数起舞
规则:我说出一句口令,如果你的学号符合它,请你快速起立。独立思考,不可提醒他人,否则视为违规。
时间:约15秒
游戏设计师
请你设计这样一些游戏:
(1)使1个人站起来
(2)使少数人站起来
(3)使一半人站起来
(4)使多数人站起来
(5)使全班人站起来
要求:1、与《因数和倍数》单元有关;2:要心中有数,设计者得有答案。
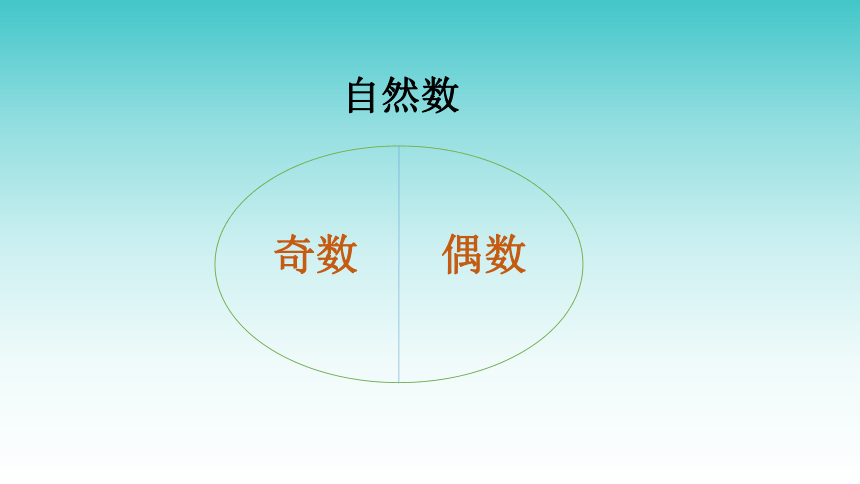
自然数
奇数
偶数
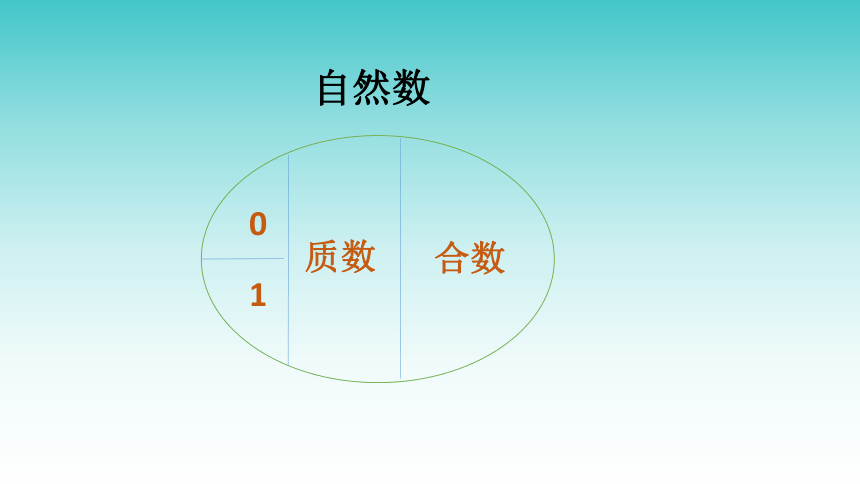
自然数
质数
合数
0
1
老师的谜题
这个人的学号,
拥有的因数个数是全班最多的!
猜猜Ta是谁?
1小时是60分,1分是60秒.“60进制”和60的因数个数有关。看看60的因数:1、2、3、4、5、6、10、12、15、20、30、60。一共12个,比100的因数还多。
由于拥有较多因数,60可以分拆成多种不同的时间长度,例如一个小时可以看作2个30分钟,3个20分钟,4个15分钟。给人们的生活带来很大的方便!
“60进制”
2
数学家在想什么
1742年,歌德巴赫提出一个猜想:每一个大于2的偶数都可以写成两个质数的和。例如,6=3+3。
我们来证明:每一个大于2,小于62的偶数都可以写成两个质数之和。每人至少写下一个例子。
歌德巴赫猜想
歌德巴赫对许多偶数进行了检验,都说明这是正确的。但是自然数是无限的,是不是对所有的自然数都正确呢?还需要加以证明。因为没被证明,它只能说是一个猜想。
从此这成了一道世界难题,有人称它为“皇冠上的明珠”。两百多年来,多少数学家企图给这个猜想作出证明,都没有成功。
到1972年我国著名的数学家陈景润向这座高峰跨上了一大步,他的研究成果处于国际领先的地位,这一成果被命名为“陈氏定理”。但是他的证明离成功只有一步之遥,就匆匆的走完了他的一生。
歌德巴赫猜想
3
火眼金睛
谁是与众不同的数
(1)1、3、5、7、8
(2)57、17、9、8、4
游戏:火眼金睛
√
√
(1)8是唯一的偶数
(2)17是唯一的质数
2是唯一的偶质数
5是唯一的奇数
6是唯一的完美数
谁是与众不同的数
2,5,6,8,16
8是唯一的立方数
16是唯一的两位数,
也是唯一的平方数。
挑战升级:
“完美数”之旅
6=1+2+3
28=1+2+4+7+14
“496”
“8128”
“33550336”
“8589869056”
......
4
十万个为什么
我们已经学习了2、3、5的倍数特征。
查漏补缺
你们知道其他数的倍数特征吗?
1的倍数特征
?
4的倍数特征
?
6的倍数特征
?
7的倍数特征
?
8的倍数特征
?
9的倍数特征
?
……
4的倍数特征:
323
284
300
一个自然数的后两位是4的倍数,这个数就是4的倍数。
整百数都是4的倍数。
√
√
6的倍数特征:
123
2018
一个数的个位是偶数,且这个数各位之和是3的
倍数。(既是2的倍数,又是3的倍数)。
2022
√
这节课,你有什么新收获?
课后找找7、8、9、10的倍数特征。
6的倍数特征:既是2的倍数又是3的倍数的数(能同时被2和3整除)
7的倍数特征:若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除
8的倍数的特征:一个数的后三位是8的倍数,这个数就是8的倍数。
9的倍数的特征:一个数各位上的数的和是9的倍数,这个数就是9的倍数。
学号游戏
玩转《因数与倍数》
1
闻“数”起舞
游戏:闻数起舞
规则:我说出一句口令,如果你的学号符合它,请你快速起立。独立思考,不可提醒他人,否则视为违规。
时间:约15秒
游戏设计师
请你设计这样一些游戏:
(1)使1个人站起来
(2)使少数人站起来
(3)使一半人站起来
(4)使多数人站起来
(5)使全班人站起来
要求:1、与《因数和倍数》单元有关;2:要心中有数,设计者得有答案。
自然数
奇数
偶数
自然数
质数
合数
0
1
老师的谜题
这个人的学号,
拥有的因数个数是全班最多的!
猜猜Ta是谁?
1小时是60分,1分是60秒.“60进制”和60的因数个数有关。看看60的因数:1、2、3、4、5、6、10、12、15、20、30、60。一共12个,比100的因数还多。
由于拥有较多因数,60可以分拆成多种不同的时间长度,例如一个小时可以看作2个30分钟,3个20分钟,4个15分钟。给人们的生活带来很大的方便!
“60进制”
2
数学家在想什么
1742年,歌德巴赫提出一个猜想:每一个大于2的偶数都可以写成两个质数的和。例如,6=3+3。
我们来证明:每一个大于2,小于62的偶数都可以写成两个质数之和。每人至少写下一个例子。
歌德巴赫猜想
歌德巴赫对许多偶数进行了检验,都说明这是正确的。但是自然数是无限的,是不是对所有的自然数都正确呢?还需要加以证明。因为没被证明,它只能说是一个猜想。
从此这成了一道世界难题,有人称它为“皇冠上的明珠”。两百多年来,多少数学家企图给这个猜想作出证明,都没有成功。
到1972年我国著名的数学家陈景润向这座高峰跨上了一大步,他的研究成果处于国际领先的地位,这一成果被命名为“陈氏定理”。但是他的证明离成功只有一步之遥,就匆匆的走完了他的一生。
歌德巴赫猜想
3
火眼金睛
谁是与众不同的数
(1)1、3、5、7、8
(2)57、17、9、8、4
游戏:火眼金睛
√
√
(1)8是唯一的偶数
(2)17是唯一的质数
2是唯一的偶质数
5是唯一的奇数
6是唯一的完美数
谁是与众不同的数
2,5,6,8,16
8是唯一的立方数
16是唯一的两位数,
也是唯一的平方数。
挑战升级:
“完美数”之旅
6=1+2+3
28=1+2+4+7+14
“496”
“8128”
“33550336”
“8589869056”
......
4
十万个为什么
我们已经学习了2、3、5的倍数特征。
查漏补缺
你们知道其他数的倍数特征吗?
1的倍数特征
?
4的倍数特征
?
6的倍数特征
?
7的倍数特征
?
8的倍数特征
?
9的倍数特征
?
……
4的倍数特征:
323
284
300
一个自然数的后两位是4的倍数,这个数就是4的倍数。
整百数都是4的倍数。
√
√
6的倍数特征:
123
2018
一个数的个位是偶数,且这个数各位之和是3的
倍数。(既是2的倍数,又是3的倍数)。
2022
√
这节课,你有什么新收获?
课后找找7、8、9、10的倍数特征。
6的倍数特征:既是2的倍数又是3的倍数的数(能同时被2和3整除)
7的倍数特征:若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除
8的倍数的特征:一个数的后三位是8的倍数,这个数就是8的倍数。
9的倍数的特征:一个数各位上的数的和是9的倍数,这个数就是9的倍数。
