2019-2020学年山东省德州市禹城市八年级下学期期末数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年山东省德州市禹城市八年级下学期期末数学试卷 (word版,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览




文档简介
2019-2020学年山东德州市禹城市八年级第二学期期末数学试卷
一、选择题(共12小题).
1.的倒数是( )
A. B. C.﹣ D.﹣
2.如图,在△ABC中,点D,E分别是边AB,AC的中点,已知DE=3,则BC的长为( )
A.3 B.4 C.6 D.5
3.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30° C.35° D.40°
4.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
5.已知,直线y=kx+b经过点A(﹣1,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
A.x<﹣2 B.﹣2<x<﹣1 C.﹣2<x<0 D.﹣1<x<0
6.下列说法中能判定四边形是矩形的是( )
A.有两个角为直角的四边形
B.对角线互相平分的四边形
C.对角线相等的四边形
D.四个角都相等的四边形
7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )
A.2 B.3 C.4 D.5
8.如图,四边形ABCD中,∠ADC=90°,AE=BE,BF=CF,连接EF,AD=3,CD=1,则EF的长为( )
A. B. C. D.
9.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 2.5 2.5 6.4 7.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
10.直线y=﹣x+1不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.三个正方形的面积如图所示,则面积为A的正方形的边长为( )
A.164 B.36 C.8 D.6
12.如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
二、填空题(共24分)
13.已知=0,则a2﹣b2020= .
14.已知一次函数y=(2m﹣1)x﹣1+3m(m为常数),当x<2时,y>0,则m的取值范围为 .
15.已知在Rt△ABC中,∠C=90°,AC=BC=,直线L过AB中点O,过点A、C分别向直线L作垂线,垂足分别为E、F.若CF=1,则EF= .
16.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图,若返回时上、下坡的速度保持不变,那么小明从学校骑车回家用的时间是 分钟.
17.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 .
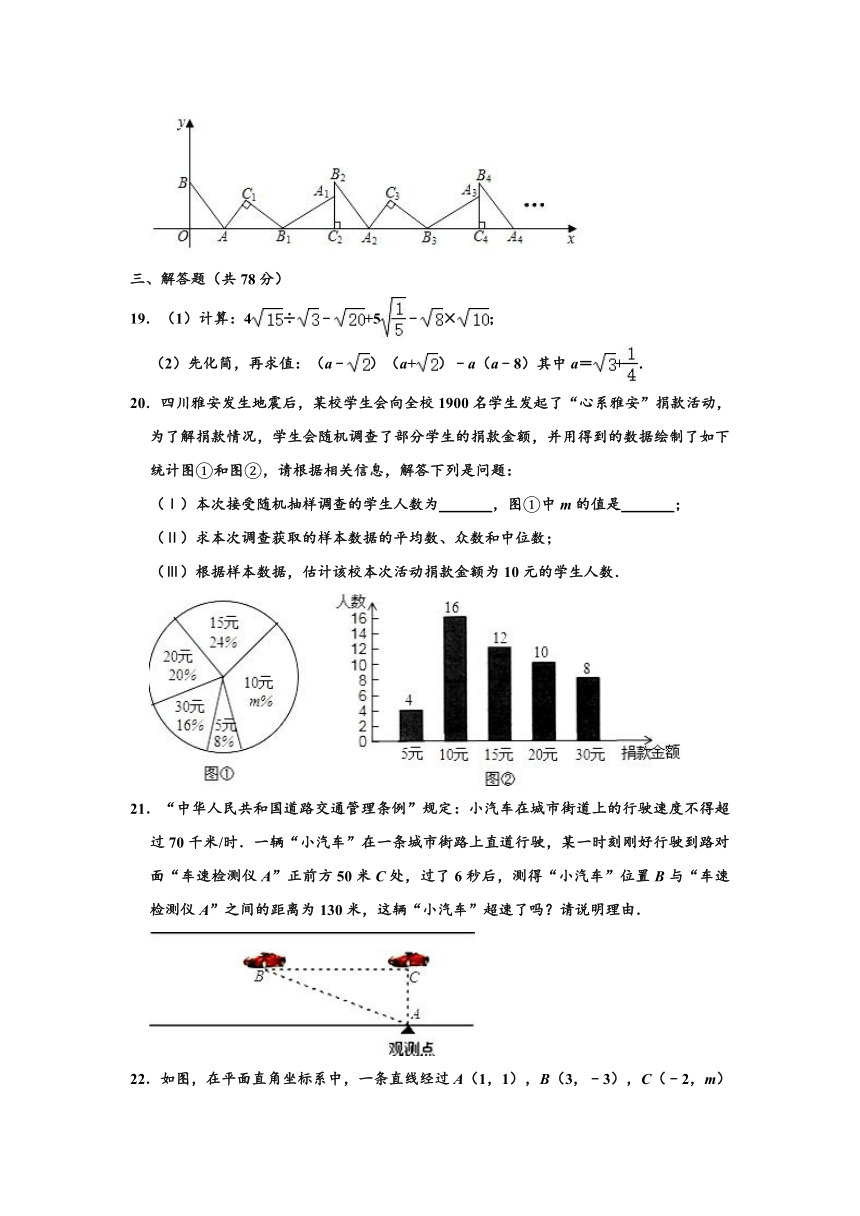
18.如图,在平面直角坐标系中,将△ABC绕点A顺时针旋转到△A1B1C1的位置,点B,O(分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去,…,若点A(,0),B(0,2),则点B2020的坐标为 .
三、解答题(共78分)
19.(1)计算:4÷﹣+5﹣×;
(2)先化简,再求值:(a﹣)(a+)﹣a(a﹣8)其中a=+.
20.四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
21.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米/时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
22.如图,在平面直角坐标系中,一条直线经过A(1,1),B(3,﹣3),C(﹣2,m)三点.
(1)求m的值;
(2)设这条直线与y轴相交于点D,求△OCD的面积.
23.如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
24.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 粗加工后销售 精加工后销售
每吨获利(元) 1000 2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
25.如图,在平面直角坐标系中,矩形OABC的顶点O是坐标原点,OA、OC分别在x轴、y轴的正半轴上,且OA=5,OC=4.
(1)如图①,将矩形沿对角线OB折叠,使得点A落在点D处,OD与CB相交于点E,请问重叠部分△OBE是什么三角形?说明你的理由:并求出这个三角形的面积;
(2)如图②,点E、F分别是OC、OA边上的点,将△OEF沿EF折叠,使得点O正好落在BC边上的D点,过点D作DH⊥OA,交EF于点G,交OA于点H,若CD=2,求点G的坐标;
(3)如图③,照(2)中条件,当点E、F在OC、OA上移动时,点D也在边BC上随之移动,请直接写出BD的取值范围.
参考答案
一、单选题(共12小题).
1.的倒数是( )
A. B. C.﹣ D.﹣
解:由×=1,得的倒数是,
故选:B.
2.如图,在△ABC中,点D,E分别是边AB,AC的中点,已知DE=3,则BC的长为( )
A.3 B.4 C.6 D.5
解:∵D、E分别是AB、AC的中点.
∴DE是△ABC的中位线,
∴BC=2DE,
∵DE=3,
∴BC=2×3=6.
故选:C.
3.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30° C.35° D.40°
解:∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,
∴∠A′OA=45°,∠AOB=∠A′OB′=15°,
∴∠AOB′=∠A′OA﹣∠A′OB′=45°﹣15°=30°,
故选:B.
4.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
解:∵AE平分∠BAD交BC边于点E,
∴∠BAE=∠EAD,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=5,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=3,
∴EC=BC﹣BE=5﹣3=2,
故选:B.
5.已知,直线y=kx+b经过点A(﹣1,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
A.x<﹣2 B.﹣2<x<﹣1 C.﹣2<x<0 D.﹣1<x<0
解:如图,
当﹣2<x<﹣1时,2x<kx+b<0成立.
故选:B.
6.下列说法中能判定四边形是矩形的是( )
A.有两个角为直角的四边形
B.对角线互相平分的四边形
C.对角线相等的四边形
D.四个角都相等的四边形
解:A、有3个角为直角的四边形是矩形,故错误;
B、对角线互相平分的平行四边形是矩形,故错误;
C、对角线相等的平行四边形,故错误;
D、四个角都相等的四边形是矩形,故正确;
故选:D.
7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )
A.2 B.3 C.4 D.5
解:∵这组数据有唯一的众数4,
∴x=4,
将数据从小到大排列为:1,2,3,3,4,4,4,
则中位数为:3.
故选:B.
8.如图,四边形ABCD中,∠ADC=90°,AE=BE,BF=CF,连接EF,AD=3,CD=1,则EF的长为( )
A. B. C. D.
解:连接AC,
∵∠ADC=90°,AD=3,CD=1,
∴AC==,
∵AE=BE,BF=CF,
∴EF=AC=,
故选:B.
9.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 2.5 2.5 6.4 7.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
解:∵甲和丙的平均数大于乙和丁的平均数,
∴从甲和丙中选择一人参加比赛,
∵甲的方差小于丙的方差,
∴选择甲参赛,
故选:A.
10.直线y=﹣x+1不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵直线y=﹣x+1中,k=﹣1<0,b=1>0,
∴直线的图象经过第一,二,四象限.
∴不经过第三象限,
故选:C.
11.三个正方形的面积如图所示,则面积为A的正方形的边长为( )
A.164 B.36 C.8 D.6
解:由勾股定理得,BC2=CD2﹣BD2=110﹣64=36,
即面积为A的正方形的边长==6,
故选:D.
12.如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
【解答】解;连接EF交AC于O,
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,,
∴△CFO≌△AEO,
∴AO=CO,
∵AC==4,
∴AO=AC=2,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴,
∴,
∴AE=5.
方法二:应连接EF得EF⊥AC 易证EF垂直平分AC 连接CE,得CE=AE,
设CE=AE=x,EB=8﹣x,BC=4,利用勾股定理求得x=5即可.
故选:C.
二、填空题(共24分)
13.已知=0,则a2﹣b2020= ﹣ .
解:∵=0,
∴2a﹣1=0,b+1=0,
解得:a=,b=﹣1,
∴a2﹣b2020=()2﹣(﹣1)2020=﹣,
故答案为:﹣.
14.已知一次函数y=(2m﹣1)x﹣1+3m(m为常数),当x<2时,y>0,则m的取值范围为 ≤m< .
解:当y=0时,(2m﹣1)x﹣1+3m=0,
解得x=,
∵x<2时,y>0,
∴2m﹣1<0,≥2,
∴≤m<.
故答案为≤m<.
15.已知在Rt△ABC中,∠C=90°,AC=BC=,直线L过AB中点O,过点A、C分别向直线L作垂线,垂足分别为E、F.若CF=1,则EF= 1或3 .
解:①如图1中,当点A、C在直线l的同侧时,连接CO.
∵CA=CB=,∠ACB=90°,OA=OB,
∴OC⊥AB,AB=2,
OC=OA=OB=,
∵∠AOE+∠EAO=90°,∠AOE+∠COF=90°,
∴∠EAO=∠COF,
∵∠AEO=∠CFO=90°,
∴△AEO≌△OFC,
∴CF=OE=1,AE=OF
∴AE==2,
∴OF=AE=2,
∴EF=3.
②如图2中,当点A、C在直线l的异侧时,连接CO.
∵CA=CB=,∠ACB=90°,OA=OB
∴OC⊥AB,AB=2,
OC=OA=OB=,
同法可证:△AEO≌△OFC,
∴CF=OE=1,AE=OF
∴AE==2,
∴OF=AE=2,
∴EF=2﹣1=1.
故答案为1或3.
16.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图,若返回时上、下坡的速度保持不变,那么小明从学校骑车回家用的时间是 37.2 分钟.
解:由图中可以看出:上坡速度为:=2百米/分,下坡速度为:=5百米/分,
返回途中,上下坡的路程正好相反,所用时间为:+=7.2+30=37.2分.
故答案为:37.2.
17.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 5 .
解:如图:
作ME⊥AC交AD于E,连接EN,
则EN就是PM+PN的最小值,
∵M、N分别是AB、BC的中点,
∴BN=BM=AM,
∵ME⊥AC交AD于E,
∴AE=AM,
∴AE=BN,AE∥BN,
∴四边形ABNE是平行四边形,
∴EN=AB,EN∥AB,
而由题意可知,可得AB==5,
∴EN=AB=5,
∴PM+PN的最小值为5.
故答案为:5.
18.如图,在平面直角坐标系中,将△ABC绕点A顺时针旋转到△A1B1C1的位置,点B,O(分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去,…,若点A(,0),B(0,2),则点B2020的坐标为 (6060,2) .
解:∵AO=,BO=2,
∴AB===,
∴OA+AB1+B1C2=++2=6,
∴B2的横坐标为:6,且B2C2=2,
∴B4的横坐标为:2×6=12,
∴点B2020的横坐标为:1010×6=6060.
∴点B2020的纵坐标为:2.
故答案为:(6060,2).
三、解答题(共78分)
19.(1)计算:4÷﹣+5﹣×;
(2)先化简,再求值:(a﹣)(a+)﹣a(a﹣8)其中a=+.
解:(1)4÷﹣+5﹣×
=4﹣2+﹣
=4﹣2+﹣4
=﹣;
(2)(a﹣)(a+)﹣a(a﹣8)
=a2﹣2﹣a2+8a
=8a﹣2,
当a=+时,原式=8×(+)﹣2=8.
20.四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 50 ,图①中m的值是 32 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
解:(1)根据条形图4+16+12+10+8=50(人),
m=100﹣20﹣24﹣16﹣8=32;
(2)∵=(5×4+10×16+15×12+20×10+30×8)=16,
∴这组数据的平均数为:16,
∵在这组样本数据中,10出现次数最多为16次,
∴这组数据的众数为:10,
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是15,
∴这组数据的中位数为:(15+15)=15;
(3)∵在50名学生中,捐款金额为10元的学生人数比例为32%,
∴由样本数据,估计该校1900名学生中捐款金额为10元的学生人数比例为32%,有1900×32%=608,
∴该校本次活动捐款金额为10元的学生约有608名.
故答案为:50,32.
21.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米/时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
解:由题意知,AB=130米,AC=50米,
且在Rt△ABC中,AB是斜边,
根据勾股定理AB2=BC2+AC2,
可以求得:BC=120米=0.12千米,
且6秒=时,
所以速度为=72千米/时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米/时.
22.如图,在平面直角坐标系中,一条直线经过A(1,1),B(3,﹣3),C(﹣2,m)三点.
(1)求m的值;
(2)设这条直线与y轴相交于点D,求△OCD的面积.
解:(1)设直线的解析式为y=kx+b,把A(1,1),B(3,﹣3)代入,可得:,
解得:,
所以直线解析式为:y=﹣2x+3,
把C(﹣2,m)代入y=﹣2x+3中,得:m=7;
(2)令x=0,则y=3,
所以直线与y轴的交点坐标为(0,3),
由(1)得点C的坐标为(﹣2,7),
所以△OCD的面积==3.
23.如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
解:(1)如图,点E、F为所作.
(2)四边形AFCE为菱形.理由如下:
∵EF垂直平分AC,
∴AE=CE,AF=CF,
∴EF平分∠AFC,即∠AFE=∠CFE,
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴AE=EC=CF=AF,
∴四边形AFCE为菱形.
24.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 粗加工后销售 精加工后销售
每吨获利(元) 1000 2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
解:(1)设应安排x天进行精加工,y天进行粗加工,
根据题意得,
解得,
答:应安排4天进行精加工,8天进行粗加工.
(2)①精加工m吨,则粗加工(140﹣m)吨,根据题意得W=2000m+1000(140﹣m)
=1000m+140000
②∵要求在不超过10天的时间内将所有蔬菜加工完,
∴,解得m≤5
∴0≤m≤5,
又∵在一次函数W=1000m+140000中,k=1000>0,
∴W随m的增大而增大,
∴当m=5时,W最大=1000×5+140000=145000.
∴精加工天数为5÷5=1,
粗加工天数为(140﹣5)÷15=9.
∴安排1天进行精加工,9天进行粗加工,可以获得最多利润为145000元.
25.如图,在平面直角坐标系中,矩形OABC的顶点O是坐标原点,OA、OC分别在x轴、y轴的正半轴上,且OA=5,OC=4.
(1)如图①,将矩形沿对角线OB折叠,使得点A落在点D处,OD与CB相交于点E,请问重叠部分△OBE是什么三角形?说明你的理由:并求出这个三角形的面积;
(2)如图②,点E、F分别是OC、OA边上的点,将△OEF沿EF折叠,使得点O正好落在BC边上的D点,过点D作DH⊥OA,交EF于点G,交OA于点H,若CD=2,求点G的坐标;
(3)如图③,照(2)中条件,当点E、F在OC、OA上移动时,点D也在边BC上随之移动,请直接写出BD的取值范围.
解:(1)如图①中,结论:△OBE是等腰三角形.
理由:∵四边形OABC是矩形,
∴OA=BC=5,OC=AB=4,∠OCB=90°,BC∥OA,
∴∠CBO=∠AOB,
由翻折的性质可知,∠AOB=∠BOE,
∴∠EBO=∠EOB,
∴EB=EC,
∴△EOB是等腰三角形.
设EB=OE=x,则CE=5﹣x,
在Rt△EOC中,则有x2=42+(5﹣x)2,
解得x=4.1,
∴S△EOB=×4.1×4=8.2.
(2)如图②中,
∵DH⊥OF,
∴DH∥OC,
∴∠OEG=∠EGD,
由翻折的性质可知,∠OEG=∠DEG,
∴∠DEG=∠DGE,
∴DE=DG,
∵EO=ED,
∴OE=DE=DG,设OE=DE=DG=x,
在Rt△EDC中,则有x2=22+(4﹣x)2,
解得x=,
∵四边形OCDH是矩形,
∴DH=OC=4,CD=OH=2,
∴GH=4﹣=,
∴G(2,).
(3)当点E与C重合时,BD的值最小,最小值为1,
当点F与A重合时,BD的值最大,最大值为3,
∴BD的取值范围为:1≤BD≤3.
一、选择题(共12小题).
1.的倒数是( )
A. B. C.﹣ D.﹣
2.如图,在△ABC中,点D,E分别是边AB,AC的中点,已知DE=3,则BC的长为( )
A.3 B.4 C.6 D.5
3.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30° C.35° D.40°
4.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
5.已知,直线y=kx+b经过点A(﹣1,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
A.x<﹣2 B.﹣2<x<﹣1 C.﹣2<x<0 D.﹣1<x<0
6.下列说法中能判定四边形是矩形的是( )
A.有两个角为直角的四边形
B.对角线互相平分的四边形
C.对角线相等的四边形
D.四个角都相等的四边形
7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )
A.2 B.3 C.4 D.5
8.如图,四边形ABCD中,∠ADC=90°,AE=BE,BF=CF,连接EF,AD=3,CD=1,则EF的长为( )
A. B. C. D.
9.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 2.5 2.5 6.4 7.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
10.直线y=﹣x+1不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.三个正方形的面积如图所示,则面积为A的正方形的边长为( )
A.164 B.36 C.8 D.6
12.如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
二、填空题(共24分)
13.已知=0,则a2﹣b2020= .
14.已知一次函数y=(2m﹣1)x﹣1+3m(m为常数),当x<2时,y>0,则m的取值范围为 .
15.已知在Rt△ABC中,∠C=90°,AC=BC=,直线L过AB中点O,过点A、C分别向直线L作垂线,垂足分别为E、F.若CF=1,则EF= .
16.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图,若返回时上、下坡的速度保持不变,那么小明从学校骑车回家用的时间是 分钟.
17.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 .
18.如图,在平面直角坐标系中,将△ABC绕点A顺时针旋转到△A1B1C1的位置,点B,O(分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去,…,若点A(,0),B(0,2),则点B2020的坐标为 .
三、解答题(共78分)
19.(1)计算:4÷﹣+5﹣×;
(2)先化简,再求值:(a﹣)(a+)﹣a(a﹣8)其中a=+.
20.四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
21.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米/时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
22.如图,在平面直角坐标系中,一条直线经过A(1,1),B(3,﹣3),C(﹣2,m)三点.
(1)求m的值;
(2)设这条直线与y轴相交于点D,求△OCD的面积.
23.如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
24.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 粗加工后销售 精加工后销售
每吨获利(元) 1000 2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
25.如图,在平面直角坐标系中,矩形OABC的顶点O是坐标原点,OA、OC分别在x轴、y轴的正半轴上,且OA=5,OC=4.
(1)如图①,将矩形沿对角线OB折叠,使得点A落在点D处,OD与CB相交于点E,请问重叠部分△OBE是什么三角形?说明你的理由:并求出这个三角形的面积;
(2)如图②,点E、F分别是OC、OA边上的点,将△OEF沿EF折叠,使得点O正好落在BC边上的D点,过点D作DH⊥OA,交EF于点G,交OA于点H,若CD=2,求点G的坐标;
(3)如图③,照(2)中条件,当点E、F在OC、OA上移动时,点D也在边BC上随之移动,请直接写出BD的取值范围.
参考答案
一、单选题(共12小题).
1.的倒数是( )
A. B. C.﹣ D.﹣
解:由×=1,得的倒数是,
故选:B.
2.如图,在△ABC中,点D,E分别是边AB,AC的中点,已知DE=3,则BC的长为( )
A.3 B.4 C.6 D.5
解:∵D、E分别是AB、AC的中点.
∴DE是△ABC的中位线,
∴BC=2DE,
∵DE=3,
∴BC=2×3=6.
故选:C.
3.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30° C.35° D.40°
解:∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,
∴∠A′OA=45°,∠AOB=∠A′OB′=15°,
∴∠AOB′=∠A′OA﹣∠A′OB′=45°﹣15°=30°,
故选:B.
4.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
解:∵AE平分∠BAD交BC边于点E,
∴∠BAE=∠EAD,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=5,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=3,
∴EC=BC﹣BE=5﹣3=2,
故选:B.
5.已知,直线y=kx+b经过点A(﹣1,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
A.x<﹣2 B.﹣2<x<﹣1 C.﹣2<x<0 D.﹣1<x<0
解:如图,
当﹣2<x<﹣1时,2x<kx+b<0成立.
故选:B.
6.下列说法中能判定四边形是矩形的是( )
A.有两个角为直角的四边形
B.对角线互相平分的四边形
C.对角线相等的四边形
D.四个角都相等的四边形
解:A、有3个角为直角的四边形是矩形,故错误;
B、对角线互相平分的平行四边形是矩形,故错误;
C、对角线相等的平行四边形,故错误;
D、四个角都相等的四边形是矩形,故正确;
故选:D.
7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )
A.2 B.3 C.4 D.5
解:∵这组数据有唯一的众数4,
∴x=4,
将数据从小到大排列为:1,2,3,3,4,4,4,
则中位数为:3.
故选:B.
8.如图,四边形ABCD中,∠ADC=90°,AE=BE,BF=CF,连接EF,AD=3,CD=1,则EF的长为( )
A. B. C. D.
解:连接AC,
∵∠ADC=90°,AD=3,CD=1,
∴AC==,
∵AE=BE,BF=CF,
∴EF=AC=,
故选:B.
9.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 2.5 2.5 6.4 7.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
解:∵甲和丙的平均数大于乙和丁的平均数,
∴从甲和丙中选择一人参加比赛,
∵甲的方差小于丙的方差,
∴选择甲参赛,
故选:A.
10.直线y=﹣x+1不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵直线y=﹣x+1中,k=﹣1<0,b=1>0,
∴直线的图象经过第一,二,四象限.
∴不经过第三象限,
故选:C.
11.三个正方形的面积如图所示,则面积为A的正方形的边长为( )
A.164 B.36 C.8 D.6
解:由勾股定理得,BC2=CD2﹣BD2=110﹣64=36,
即面积为A的正方形的边长==6,
故选:D.
12.如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
【解答】解;连接EF交AC于O,
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,,
∴△CFO≌△AEO,
∴AO=CO,
∵AC==4,
∴AO=AC=2,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴,
∴,
∴AE=5.
方法二:应连接EF得EF⊥AC 易证EF垂直平分AC 连接CE,得CE=AE,
设CE=AE=x,EB=8﹣x,BC=4,利用勾股定理求得x=5即可.
故选:C.
二、填空题(共24分)
13.已知=0,则a2﹣b2020= ﹣ .
解:∵=0,
∴2a﹣1=0,b+1=0,
解得:a=,b=﹣1,
∴a2﹣b2020=()2﹣(﹣1)2020=﹣,
故答案为:﹣.
14.已知一次函数y=(2m﹣1)x﹣1+3m(m为常数),当x<2时,y>0,则m的取值范围为 ≤m< .
解:当y=0时,(2m﹣1)x﹣1+3m=0,
解得x=,
∵x<2时,y>0,
∴2m﹣1<0,≥2,
∴≤m<.
故答案为≤m<.
15.已知在Rt△ABC中,∠C=90°,AC=BC=,直线L过AB中点O,过点A、C分别向直线L作垂线,垂足分别为E、F.若CF=1,则EF= 1或3 .
解:①如图1中,当点A、C在直线l的同侧时,连接CO.
∵CA=CB=,∠ACB=90°,OA=OB,
∴OC⊥AB,AB=2,
OC=OA=OB=,
∵∠AOE+∠EAO=90°,∠AOE+∠COF=90°,
∴∠EAO=∠COF,
∵∠AEO=∠CFO=90°,
∴△AEO≌△OFC,
∴CF=OE=1,AE=OF
∴AE==2,
∴OF=AE=2,
∴EF=3.
②如图2中,当点A、C在直线l的异侧时,连接CO.
∵CA=CB=,∠ACB=90°,OA=OB
∴OC⊥AB,AB=2,
OC=OA=OB=,
同法可证:△AEO≌△OFC,
∴CF=OE=1,AE=OF
∴AE==2,
∴OF=AE=2,
∴EF=2﹣1=1.
故答案为1或3.
16.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图,若返回时上、下坡的速度保持不变,那么小明从学校骑车回家用的时间是 37.2 分钟.
解:由图中可以看出:上坡速度为:=2百米/分,下坡速度为:=5百米/分,
返回途中,上下坡的路程正好相反,所用时间为:+=7.2+30=37.2分.
故答案为:37.2.
17.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是 5 .
解:如图:
作ME⊥AC交AD于E,连接EN,
则EN就是PM+PN的最小值,
∵M、N分别是AB、BC的中点,
∴BN=BM=AM,
∵ME⊥AC交AD于E,
∴AE=AM,
∴AE=BN,AE∥BN,
∴四边形ABNE是平行四边形,
∴EN=AB,EN∥AB,
而由题意可知,可得AB==5,
∴EN=AB=5,
∴PM+PN的最小值为5.
故答案为:5.
18.如图,在平面直角坐标系中,将△ABC绕点A顺时针旋转到△A1B1C1的位置,点B,O(分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去,…,若点A(,0),B(0,2),则点B2020的坐标为 (6060,2) .
解:∵AO=,BO=2,
∴AB===,
∴OA+AB1+B1C2=++2=6,
∴B2的横坐标为:6,且B2C2=2,
∴B4的横坐标为:2×6=12,
∴点B2020的横坐标为:1010×6=6060.
∴点B2020的纵坐标为:2.
故答案为:(6060,2).
三、解答题(共78分)
19.(1)计算:4÷﹣+5﹣×;
(2)先化简,再求值:(a﹣)(a+)﹣a(a﹣8)其中a=+.
解:(1)4÷﹣+5﹣×
=4﹣2+﹣
=4﹣2+﹣4
=﹣;
(2)(a﹣)(a+)﹣a(a﹣8)
=a2﹣2﹣a2+8a
=8a﹣2,
当a=+时,原式=8×(+)﹣2=8.
20.四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 50 ,图①中m的值是 32 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
解:(1)根据条形图4+16+12+10+8=50(人),
m=100﹣20﹣24﹣16﹣8=32;
(2)∵=(5×4+10×16+15×12+20×10+30×8)=16,
∴这组数据的平均数为:16,
∵在这组样本数据中,10出现次数最多为16次,
∴这组数据的众数为:10,
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是15,
∴这组数据的中位数为:(15+15)=15;
(3)∵在50名学生中,捐款金额为10元的学生人数比例为32%,
∴由样本数据,估计该校1900名学生中捐款金额为10元的学生人数比例为32%,有1900×32%=608,
∴该校本次活动捐款金额为10元的学生约有608名.
故答案为:50,32.
21.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米/时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
解:由题意知,AB=130米,AC=50米,
且在Rt△ABC中,AB是斜边,
根据勾股定理AB2=BC2+AC2,
可以求得:BC=120米=0.12千米,
且6秒=时,
所以速度为=72千米/时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米/时.
22.如图,在平面直角坐标系中,一条直线经过A(1,1),B(3,﹣3),C(﹣2,m)三点.
(1)求m的值;
(2)设这条直线与y轴相交于点D,求△OCD的面积.
解:(1)设直线的解析式为y=kx+b,把A(1,1),B(3,﹣3)代入,可得:,
解得:,
所以直线解析式为:y=﹣2x+3,
把C(﹣2,m)代入y=﹣2x+3中,得:m=7;
(2)令x=0,则y=3,
所以直线与y轴的交点坐标为(0,3),
由(1)得点C的坐标为(﹣2,7),
所以△OCD的面积==3.
23.如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
解:(1)如图,点E、F为所作.
(2)四边形AFCE为菱形.理由如下:
∵EF垂直平分AC,
∴AE=CE,AF=CF,
∴EF平分∠AFC,即∠AFE=∠CFE,
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴AE=EC=CF=AF,
∴四边形AFCE为菱形.
24.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 粗加工后销售 精加工后销售
每吨获利(元) 1000 2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
解:(1)设应安排x天进行精加工,y天进行粗加工,
根据题意得,
解得,
答:应安排4天进行精加工,8天进行粗加工.
(2)①精加工m吨,则粗加工(140﹣m)吨,根据题意得W=2000m+1000(140﹣m)
=1000m+140000
②∵要求在不超过10天的时间内将所有蔬菜加工完,
∴,解得m≤5
∴0≤m≤5,
又∵在一次函数W=1000m+140000中,k=1000>0,
∴W随m的增大而增大,
∴当m=5时,W最大=1000×5+140000=145000.
∴精加工天数为5÷5=1,
粗加工天数为(140﹣5)÷15=9.
∴安排1天进行精加工,9天进行粗加工,可以获得最多利润为145000元.
25.如图,在平面直角坐标系中,矩形OABC的顶点O是坐标原点,OA、OC分别在x轴、y轴的正半轴上,且OA=5,OC=4.
(1)如图①,将矩形沿对角线OB折叠,使得点A落在点D处,OD与CB相交于点E,请问重叠部分△OBE是什么三角形?说明你的理由:并求出这个三角形的面积;
(2)如图②,点E、F分别是OC、OA边上的点,将△OEF沿EF折叠,使得点O正好落在BC边上的D点,过点D作DH⊥OA,交EF于点G,交OA于点H,若CD=2,求点G的坐标;
(3)如图③,照(2)中条件,当点E、F在OC、OA上移动时,点D也在边BC上随之移动,请直接写出BD的取值范围.
解:(1)如图①中,结论:△OBE是等腰三角形.
理由:∵四边形OABC是矩形,
∴OA=BC=5,OC=AB=4,∠OCB=90°,BC∥OA,
∴∠CBO=∠AOB,
由翻折的性质可知,∠AOB=∠BOE,
∴∠EBO=∠EOB,
∴EB=EC,
∴△EOB是等腰三角形.
设EB=OE=x,则CE=5﹣x,
在Rt△EOC中,则有x2=42+(5﹣x)2,
解得x=4.1,
∴S△EOB=×4.1×4=8.2.
(2)如图②中,
∵DH⊥OF,
∴DH∥OC,
∴∠OEG=∠EGD,
由翻折的性质可知,∠OEG=∠DEG,
∴∠DEG=∠DGE,
∴DE=DG,
∵EO=ED,
∴OE=DE=DG,设OE=DE=DG=x,
在Rt△EDC中,则有x2=22+(4﹣x)2,
解得x=,
∵四边形OCDH是矩形,
∴DH=OC=4,CD=OH=2,
∴GH=4﹣=,
∴G(2,).
(3)当点E与C重合时,BD的值最小,最小值为1,
当点F与A重合时,BD的值最大,最大值为3,
∴BD的取值范围为:1≤BD≤3.
同课章节目录
