2019-2020学年山东省临沂市河东区七年级下学期期末数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年山东省临沂市河东区七年级下学期期末数学试卷 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 932.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 07:40:38 | ||
图片预览



文档简介
2019-2020学年山东临沂市河东区七年级第二学期期末数学试卷
一、选择题(共14小题).
1.为了解某校2000名学生的视力情况,从中随机调查了400名学生的视力情况,下列说法正确的是( )
A.该调查的方式是抽样调查
B.该调查的方式是普查
C.2000名学生是样本
D.样本容量是400名学生
2.点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
3.a,b都是实数,且a<b,则下列不等式的变形正确的是( )
A.a+x>b+x B.﹣a+1<﹣b+1 C.3a<3b D.>
4.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
5.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
6.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140°
B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向右拐40°,第二次向右拐40°
7.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
A. B.1﹣ C. D.2﹣
8.在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段PQ∥y轴且PQ=5,则点Q的坐标是( )
A.(﹣3,7)或(﹣3,﹣3) B.(﹣3,3)或(﹣7,3)
C.(﹣2,2)或(﹣8,2) D.(﹣2,8)或(﹣2,﹣2)
9.已知△ABC内一点P(a,b)经过平移后对应点P′(c,d),顶点A(﹣2,2)在经过此次平移后对应点A′(5,﹣4),则a﹣b﹣c+d的值为( )
A.13 B.﹣13 C.1 D.﹣1
10.已知方程组,则5x﹣5y+10的值是( )
A.5 B.﹣5 C.15 D.25
11.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(﹣5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(﹣5)+②×2
12.若不等式组无解,那么m的取值范围是( )
A.m≤2 B.m≥2 C.m<2 D.m>2
13.已知关于x的不等式组的解集为3≤x<5,则的值为( )
A.﹣2 B.﹣ C.﹣4 D.﹣
14.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,第n次移动到An,则△OA3A2020的面积是( )
A.504.5m2 B.505m2 C.505.5m2D D.1010m2
二、填空题(本大题共5小题,每小题3分,共15分)
15.相反数的立方根是 .
16.把40个数据分成6组,第一到第四组的频数分别为9,5,8,6,第五组的频率是0.1,则第六组的频数是 .
17.已知方程组的解x,y满足x+3y=3.则m的值是 .
18.如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿着BC平移至△DEF的位置,若CF=3,则DG= .
19.已知关于x的不等式组只有五个整数解,则实数a的取值范围是 .
三、解答题(本大题共7小题,共63分)
20.计算:+|2﹣|++6÷(﹣)
21.解方程组:.
22.解不等式组,将其解集在数轴上表示出来,并写出这个不等式组的最小整数解.
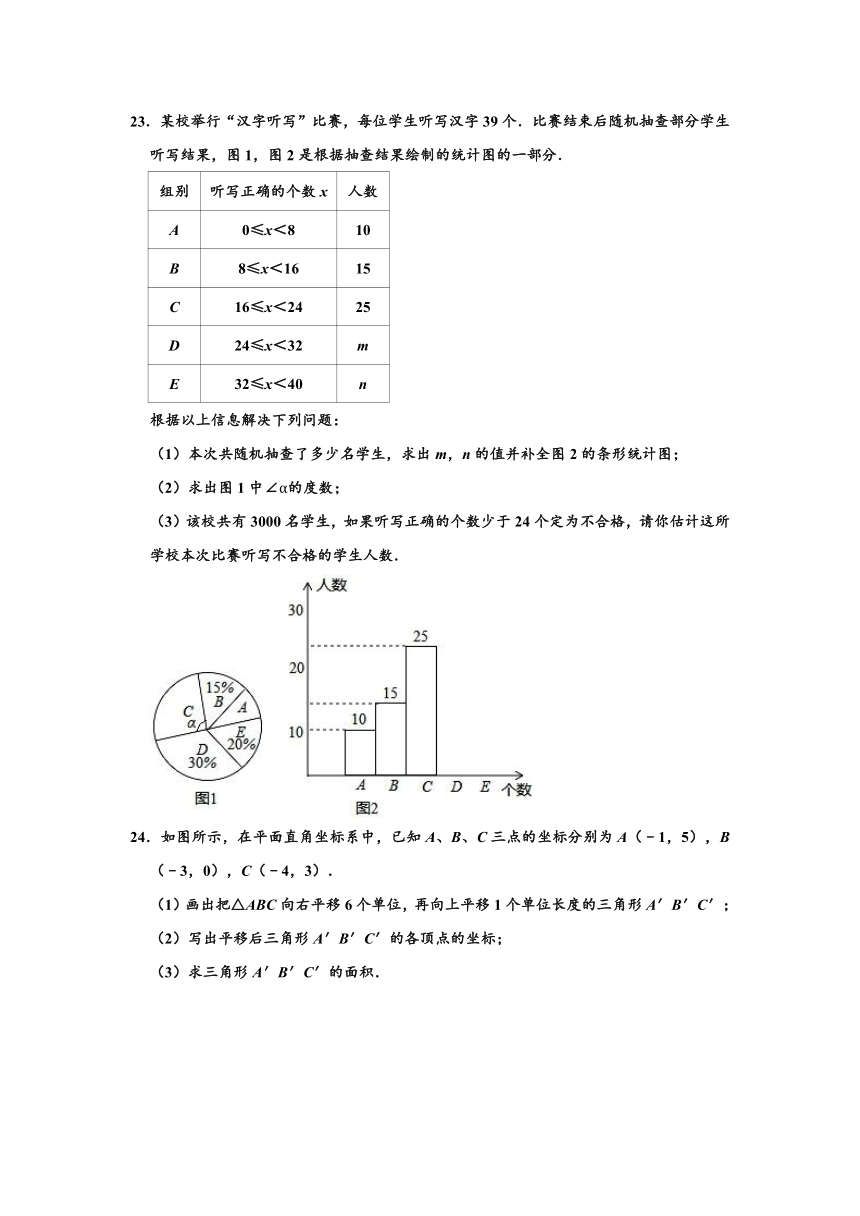
23.某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别 听写正确的个数x 人数
A 0≤x<8 10
B 8≤x<16 15
C 16≤x<24 25
D 24≤x<32 m
E 32≤x<40 n
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中∠α的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
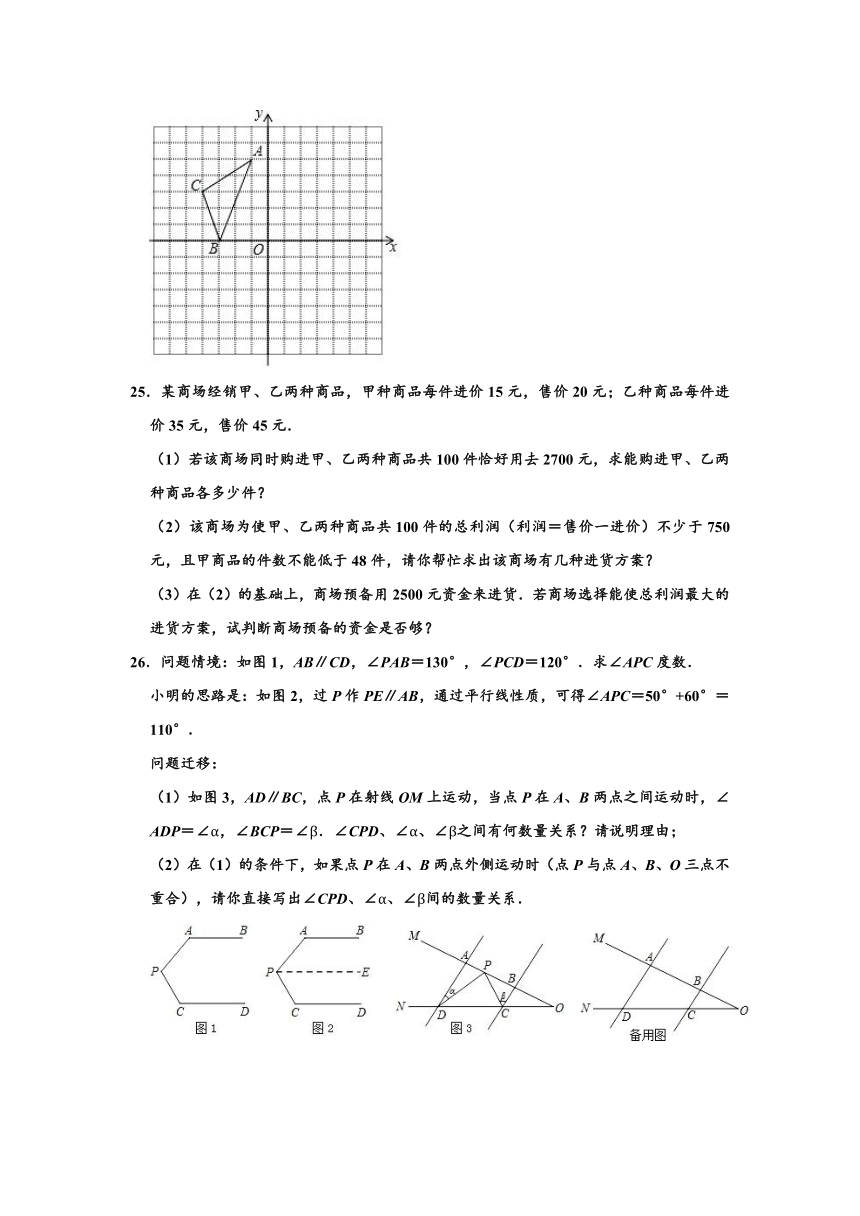
24.如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积.
25.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价一进价)不少于750元,且甲商品的件数不能低于48件,请你帮忙求出该商场有几种进货方案?
(3)在(2)的基础上,商场预备用2500元资金来进货.若商场选择能使总利润最大的进货方案,试判断商场预备的资金是否够?
26.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
参考答案
一、选择题(共14小题).
1.为了解某校2000名学生的视力情况,从中随机调查了400名学生的视力情况,下列说法正确的是( )
A.该调查的方式是抽样调查
B.该调查的方式是普查
C.2000名学生是样本
D.样本容量是400名学生
解:A、该调查的方式是抽样调查,故A正确;
B、该调查的方式不是普查,故B错误;
C、400名学生的视力情况是样本,故C错误;
D、样本容量是400,故D错误;
故选:A.
2.点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
解:已知点P(2,﹣3),
则点P关于原点对称的点的坐标是(﹣2,3),
故选:C.
3.a,b都是实数,且a<b,则下列不等式的变形正确的是( )
A.a+x>b+x B.﹣a+1<﹣b+1 C.3a<3b D.>
解:A、不等式的两边都加或都减同一个整式,不等号的方向不变,故A错误;
B、不等式的两边都乘或除以同一个负数,不等号的方向改变,故B错误;
C、不等式的两边都乘以或除以同一个正数,不等号的方向不变,故C正确;
D、不等式的两边都乘以或除以同一个正数,不等号的方向不变,故D错误;
故选:C.
4.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
解:图中所示过直线外一点作已知直线的平行线,则利用了同位角相等,两直线平行的判定方法.
故选:A.
5.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵∠1=35°,
∴∠AEC=∠ABC﹣∠1=25°,
∵GH∥EF,
∴∠2=∠AEC=25°,
故选:B.
6.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140°
B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向右拐40°,第二次向右拐40°
解:A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选:B.
7.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
A. B.1﹣ C. D.2﹣
解:设点C表示的数是x,
∵数轴上表示1、的对应点分别为点A、点B,点A是BC的中点,
∴=1,解得x=2﹣.
故选:D.
8.在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段PQ∥y轴且PQ=5,则点Q的坐标是( )
A.(﹣3,7)或(﹣3,﹣3) B.(﹣3,3)或(﹣7,3)
C.(﹣2,2)或(﹣8,2) D.(﹣2,8)或(﹣2,﹣2)
解:点P到x轴的距离是2,则点P的纵坐标为±2,
点P到y轴的距离是3,则点P的纵坐标为±3,
由于点P在第二象限,故P坐标为(﹣3,2).
∵线段PQ∥y轴且PQ=5,
∴点Q的坐标是(﹣3,7)或(﹣3,﹣3)
故选:A.
9.已知△ABC内一点P(a,b)经过平移后对应点P′(c,d),顶点A(﹣2,2)在经过此次平移后对应点A′(5,﹣4),则a﹣b﹣c+d的值为( )
A.13 B.﹣13 C.1 D.﹣1
解:∵A(﹣2,2)在经过此次平移后对应点A1的坐标为(5,﹣4),
∴△ABC的平移规律为:向右平移7个单位,向下平移6个单位,
∵点P(a,b)经过平移后对应点P1(c,d),
∴a+7=c,b﹣6=d,
∴a﹣c=﹣7,b﹣d=6,
∴a﹣b﹣c+d=a﹣c﹣(b﹣d)=﹣7﹣6=﹣13,
故选:B.
10.已知方程组,则5x﹣5y+10的值是( )
A.5 B.﹣5 C.15 D.25
解:,
则①﹣②得:
x﹣y=﹣1,
故5x﹣5y+10
=5(x﹣y)+10
=﹣5+10
=5.
故选:A.
11.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(﹣5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(﹣5)+②×2
解:利用加减消元法解方程组,要消元y,
可以将①×3+②×5;
要消去x,可以将①×(﹣5)+②×2,
故选:D.
12.若不等式组无解,那么m的取值范围是( )
A.m≤2 B.m≥2 C.m<2 D.m>2
解:
由①得,x<m,
由②得,x>2,
又因为不等式组无解,
所以m≤2.
故选:A.
13.已知关于x的不等式组的解集为3≤x<5,则的值为( )
A.﹣2 B.﹣ C.﹣4 D.﹣
解:不等式组
由①得,x≥a+b,
由②得,x<,
∴,
解得,
∴=﹣2.
故选:A.
14.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,第n次移动到An,则△OA3A2020的面积是( )
A.504.5m2 B.505m2 C.505.5m2D D.1010m2
解:由题意知OA4n=2n,
∵2020÷4=505,
∴OA2020=2×505=1010,
则△OA3A2020的面积是×1×1010=505m2,
故选:B.
二、填空题(本大题共5小题,每小题3分,共15分)
15.相反数的立方根是 ﹣2 .
解:相反数的立方根是﹣2,
故答案为:﹣2.
16.把40个数据分成6组,第一到第四组的频数分别为9,5,8,6,第五组的频率是0.1,则第六组的频数是 8 .
解:第五组的频数为:0.1×40=4,
∴第六组的频数为:40﹣9﹣5﹣8﹣6﹣4=8,
故答案为:8
17.已知方程组的解x,y满足x+3y=3.则m的值是 1 .
解:,
则①+②得:
3y+x=2m+1,
∵x+3y=3,
∴2m+1=3,
解得:m=1.
故答案为:1.
18.如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿着BC平移至△DEF的位置,若CF=3,则DG= .
解:根据题意得,DE=AB=6,EF=BC=8,
∵CF=3,
∴EC=8﹣3=5,
∵CG∥DF.
∴EG:ED=EC:EF,
即 EG:6=5:8,
∴EG=,
∴DG=DE﹣EG=6﹣=,
故答案为:.
19.已知关于x的不等式组只有五个整数解,则实数a的取值范围是 ﹣4≤a<﹣3 .
解:解不等式x﹣a>0,得:x>a,
解不等式1﹣2x>﹣3,得:x<2,
∵只有五个整数解,
∴﹣4≤a<﹣3,
故答案为:﹣4≤a<﹣3.
三、解答题(本大题共7小题,共63分)
20.计算:+|2﹣|++6÷(﹣)
解:原式=9+2﹣﹣3﹣6×
=9+2﹣﹣3﹣8
=﹣.
21.解方程组:.
解:原方程组可变化成,
①×3+②×2,得
17m=306,
m=18,
把m=18代入①,得
n=12,
所以方程组的解是.
22.解不等式组,将其解集在数轴上表示出来,并写出这个不等式组的最小整数解.
解:,
由①解得x≤3
由②解得x>﹣2
不等式组的解集在数轴上表示如图所示
所以,原不等式组的解集为﹣2<x≤3
不等式组的最小整数解为﹣1.
23.某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别 听写正确的个数x 人数
A 0≤x<8 10
B 8≤x<16 15
C 16≤x<24 25
D 24≤x<32 m
E 32≤x<40 n
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中∠α的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
解:(1)15÷15%=100(名);
m=30%×100=30;
n=20%×100=20.
条形图如图所示:
(2)∠α=×360=90°.
(3)解:3000×=1500(名)
答:估计这所学校本次比赛听写不合格的学生人数有1500(名).
24.如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积.
解:(1)△A′B′C′如图所示;
(2)A′(5,6),B′(3,1),C′(2,4);
(3)△A′B′C′的面积=3×5﹣×1×3﹣×2×5﹣×2×3,
=15﹣1.5﹣5﹣3,
=15﹣9.5,
=5.5.
25.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价一进价)不少于750元,且甲商品的件数不能低于48件,请你帮忙求出该商场有几种进货方案?
(3)在(2)的基础上,商场预备用2500元资金来进货.若商场选择能使总利润最大的进货方案,试判断商场预备的资金是否够?
解:(1)设购进甲、乙两种商品分别为x件、y件,
,
解得,,
答:能购进甲、乙两种商品分别为40件,60件;
(2)设购进甲种商品a件,则购进乙种商品(100﹣a)件,
(20﹣15)a+(45﹣35)(100﹣a)≥750,
解得,a≤50,
又∵a≥48,a为整数,
∴a=48,49,50,
∴该商场共有三种进货方案;
(3)设设购进甲种商品a件,则购进乙种商品(100﹣a)件,利润为w元,
w=(20﹣15)a+(45﹣35)(100﹣a)=﹣5a+1000,
由(2)知a=48,49,50,
∴当a=48时,w取得最大值,此时100﹣a=52,
∴当取得最大利润时,需要花费:48×15+52×35=2540(元),
∵2540>2500,
∴商场预备的资金不够用.
26.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
【解答】(1)解:∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,
∠CPD=∠β﹣∠α;
当P在AB延长线时,
∠CPD=∠α﹣∠β.
一、选择题(共14小题).
1.为了解某校2000名学生的视力情况,从中随机调查了400名学生的视力情况,下列说法正确的是( )
A.该调查的方式是抽样调查
B.该调查的方式是普查
C.2000名学生是样本
D.样本容量是400名学生
2.点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
3.a,b都是实数,且a<b,则下列不等式的变形正确的是( )
A.a+x>b+x B.﹣a+1<﹣b+1 C.3a<3b D.>
4.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
5.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
6.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140°
B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向右拐40°,第二次向右拐40°
7.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
A. B.1﹣ C. D.2﹣
8.在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段PQ∥y轴且PQ=5,则点Q的坐标是( )
A.(﹣3,7)或(﹣3,﹣3) B.(﹣3,3)或(﹣7,3)
C.(﹣2,2)或(﹣8,2) D.(﹣2,8)或(﹣2,﹣2)
9.已知△ABC内一点P(a,b)经过平移后对应点P′(c,d),顶点A(﹣2,2)在经过此次平移后对应点A′(5,﹣4),则a﹣b﹣c+d的值为( )
A.13 B.﹣13 C.1 D.﹣1
10.已知方程组,则5x﹣5y+10的值是( )
A.5 B.﹣5 C.15 D.25
11.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(﹣5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(﹣5)+②×2
12.若不等式组无解,那么m的取值范围是( )
A.m≤2 B.m≥2 C.m<2 D.m>2
13.已知关于x的不等式组的解集为3≤x<5,则的值为( )
A.﹣2 B.﹣ C.﹣4 D.﹣
14.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,第n次移动到An,则△OA3A2020的面积是( )
A.504.5m2 B.505m2 C.505.5m2D D.1010m2
二、填空题(本大题共5小题,每小题3分,共15分)
15.相反数的立方根是 .
16.把40个数据分成6组,第一到第四组的频数分别为9,5,8,6,第五组的频率是0.1,则第六组的频数是 .
17.已知方程组的解x,y满足x+3y=3.则m的值是 .
18.如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿着BC平移至△DEF的位置,若CF=3,则DG= .
19.已知关于x的不等式组只有五个整数解,则实数a的取值范围是 .
三、解答题(本大题共7小题,共63分)
20.计算:+|2﹣|++6÷(﹣)
21.解方程组:.
22.解不等式组,将其解集在数轴上表示出来,并写出这个不等式组的最小整数解.
23.某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别 听写正确的个数x 人数
A 0≤x<8 10
B 8≤x<16 15
C 16≤x<24 25
D 24≤x<32 m
E 32≤x<40 n
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中∠α的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
24.如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积.
25.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价一进价)不少于750元,且甲商品的件数不能低于48件,请你帮忙求出该商场有几种进货方案?
(3)在(2)的基础上,商场预备用2500元资金来进货.若商场选择能使总利润最大的进货方案,试判断商场预备的资金是否够?
26.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
参考答案
一、选择题(共14小题).
1.为了解某校2000名学生的视力情况,从中随机调查了400名学生的视力情况,下列说法正确的是( )
A.该调查的方式是抽样调查
B.该调查的方式是普查
C.2000名学生是样本
D.样本容量是400名学生
解:A、该调查的方式是抽样调查,故A正确;
B、该调查的方式不是普查,故B错误;
C、400名学生的视力情况是样本,故C错误;
D、样本容量是400,故D错误;
故选:A.
2.点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
解:已知点P(2,﹣3),
则点P关于原点对称的点的坐标是(﹣2,3),
故选:C.
3.a,b都是实数,且a<b,则下列不等式的变形正确的是( )
A.a+x>b+x B.﹣a+1<﹣b+1 C.3a<3b D.>
解:A、不等式的两边都加或都减同一个整式,不等号的方向不变,故A错误;
B、不等式的两边都乘或除以同一个负数,不等号的方向改变,故B错误;
C、不等式的两边都乘以或除以同一个正数,不等号的方向不变,故C正确;
D、不等式的两边都乘以或除以同一个正数,不等号的方向不变,故D错误;
故选:C.
4.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
解:图中所示过直线外一点作已知直线的平行线,则利用了同位角相等,两直线平行的判定方法.
故选:A.
5.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵∠1=35°,
∴∠AEC=∠ABC﹣∠1=25°,
∵GH∥EF,
∴∠2=∠AEC=25°,
故选:B.
6.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140°
B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向右拐40°,第二次向右拐40°
解:A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选:B.
7.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
A. B.1﹣ C. D.2﹣
解:设点C表示的数是x,
∵数轴上表示1、的对应点分别为点A、点B,点A是BC的中点,
∴=1,解得x=2﹣.
故选:D.
8.在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段PQ∥y轴且PQ=5,则点Q的坐标是( )
A.(﹣3,7)或(﹣3,﹣3) B.(﹣3,3)或(﹣7,3)
C.(﹣2,2)或(﹣8,2) D.(﹣2,8)或(﹣2,﹣2)
解:点P到x轴的距离是2,则点P的纵坐标为±2,
点P到y轴的距离是3,则点P的纵坐标为±3,
由于点P在第二象限,故P坐标为(﹣3,2).
∵线段PQ∥y轴且PQ=5,
∴点Q的坐标是(﹣3,7)或(﹣3,﹣3)
故选:A.
9.已知△ABC内一点P(a,b)经过平移后对应点P′(c,d),顶点A(﹣2,2)在经过此次平移后对应点A′(5,﹣4),则a﹣b﹣c+d的值为( )
A.13 B.﹣13 C.1 D.﹣1
解:∵A(﹣2,2)在经过此次平移后对应点A1的坐标为(5,﹣4),
∴△ABC的平移规律为:向右平移7个单位,向下平移6个单位,
∵点P(a,b)经过平移后对应点P1(c,d),
∴a+7=c,b﹣6=d,
∴a﹣c=﹣7,b﹣d=6,
∴a﹣b﹣c+d=a﹣c﹣(b﹣d)=﹣7﹣6=﹣13,
故选:B.
10.已知方程组,则5x﹣5y+10的值是( )
A.5 B.﹣5 C.15 D.25
解:,
则①﹣②得:
x﹣y=﹣1,
故5x﹣5y+10
=5(x﹣y)+10
=﹣5+10
=5.
故选:A.
11.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(﹣5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(﹣5)+②×2
解:利用加减消元法解方程组,要消元y,
可以将①×3+②×5;
要消去x,可以将①×(﹣5)+②×2,
故选:D.
12.若不等式组无解,那么m的取值范围是( )
A.m≤2 B.m≥2 C.m<2 D.m>2
解:
由①得,x<m,
由②得,x>2,
又因为不等式组无解,
所以m≤2.
故选:A.
13.已知关于x的不等式组的解集为3≤x<5,则的值为( )
A.﹣2 B.﹣ C.﹣4 D.﹣
解:不等式组
由①得,x≥a+b,
由②得,x<,
∴,
解得,
∴=﹣2.
故选:A.
14.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,第n次移动到An,则△OA3A2020的面积是( )
A.504.5m2 B.505m2 C.505.5m2D D.1010m2
解:由题意知OA4n=2n,
∵2020÷4=505,
∴OA2020=2×505=1010,
则△OA3A2020的面积是×1×1010=505m2,
故选:B.
二、填空题(本大题共5小题,每小题3分,共15分)
15.相反数的立方根是 ﹣2 .
解:相反数的立方根是﹣2,
故答案为:﹣2.
16.把40个数据分成6组,第一到第四组的频数分别为9,5,8,6,第五组的频率是0.1,则第六组的频数是 8 .
解:第五组的频数为:0.1×40=4,
∴第六组的频数为:40﹣9﹣5﹣8﹣6﹣4=8,
故答案为:8
17.已知方程组的解x,y满足x+3y=3.则m的值是 1 .
解:,
则①+②得:
3y+x=2m+1,
∵x+3y=3,
∴2m+1=3,
解得:m=1.
故答案为:1.
18.如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿着BC平移至△DEF的位置,若CF=3,则DG= .
解:根据题意得,DE=AB=6,EF=BC=8,
∵CF=3,
∴EC=8﹣3=5,
∵CG∥DF.
∴EG:ED=EC:EF,
即 EG:6=5:8,
∴EG=,
∴DG=DE﹣EG=6﹣=,
故答案为:.
19.已知关于x的不等式组只有五个整数解,则实数a的取值范围是 ﹣4≤a<﹣3 .
解:解不等式x﹣a>0,得:x>a,
解不等式1﹣2x>﹣3,得:x<2,
∵只有五个整数解,
∴﹣4≤a<﹣3,
故答案为:﹣4≤a<﹣3.
三、解答题(本大题共7小题,共63分)
20.计算:+|2﹣|++6÷(﹣)
解:原式=9+2﹣﹣3﹣6×
=9+2﹣﹣3﹣8
=﹣.
21.解方程组:.
解:原方程组可变化成,
①×3+②×2,得
17m=306,
m=18,
把m=18代入①,得
n=12,
所以方程组的解是.
22.解不等式组,将其解集在数轴上表示出来,并写出这个不等式组的最小整数解.
解:,
由①解得x≤3
由②解得x>﹣2
不等式组的解集在数轴上表示如图所示
所以,原不等式组的解集为﹣2<x≤3
不等式组的最小整数解为﹣1.
23.某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别 听写正确的个数x 人数
A 0≤x<8 10
B 8≤x<16 15
C 16≤x<24 25
D 24≤x<32 m
E 32≤x<40 n
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中∠α的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
解:(1)15÷15%=100(名);
m=30%×100=30;
n=20%×100=20.
条形图如图所示:
(2)∠α=×360=90°.
(3)解:3000×=1500(名)
答:估计这所学校本次比赛听写不合格的学生人数有1500(名).
24.如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积.
解:(1)△A′B′C′如图所示;
(2)A′(5,6),B′(3,1),C′(2,4);
(3)△A′B′C′的面积=3×5﹣×1×3﹣×2×5﹣×2×3,
=15﹣1.5﹣5﹣3,
=15﹣9.5,
=5.5.
25.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价一进价)不少于750元,且甲商品的件数不能低于48件,请你帮忙求出该商场有几种进货方案?
(3)在(2)的基础上,商场预备用2500元资金来进货.若商场选择能使总利润最大的进货方案,试判断商场预备的资金是否够?
解:(1)设购进甲、乙两种商品分别为x件、y件,
,
解得,,
答:能购进甲、乙两种商品分别为40件,60件;
(2)设购进甲种商品a件,则购进乙种商品(100﹣a)件,
(20﹣15)a+(45﹣35)(100﹣a)≥750,
解得,a≤50,
又∵a≥48,a为整数,
∴a=48,49,50,
∴该商场共有三种进货方案;
(3)设设购进甲种商品a件,则购进乙种商品(100﹣a)件,利润为w元,
w=(20﹣15)a+(45﹣35)(100﹣a)=﹣5a+1000,
由(2)知a=48,49,50,
∴当a=48时,w取得最大值,此时100﹣a=52,
∴当取得最大利润时,需要花费:48×15+52×35=2540(元),
∵2540>2500,
∴商场预备的资金不够用.
26.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
【解答】(1)解:∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,
∠CPD=∠β﹣∠α;
当P在AB延长线时,
∠CPD=∠α﹣∠β.
同课章节目录
