2019-2020学年山东省德州市临邑县七年级下学期期末数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年山东省德州市临邑县七年级下学期期末数学试卷 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 750.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 07:48:39 | ||
图片预览



文档简介
2019-2020学年山东德州市临邑县七年级第二学期期末数学试卷
一、选择题(共12小题).
1.9的算术平方根是( )
A.±3 B.3 C.﹣3 D.
2.实数、、、﹣π、0、0.101001…中,无理数个数为( )
A.1 B.2 C.3 D.4
3.下列调查中,适宜采用普查方式的是( )
A.调查“奔跑吧,兄弟”节目的收视率
B.调查沧州市民对武术的喜爱
C.调查河北省七年级学生的身高
D.调查我国探月工程“嫦娥四号”的零部件质量
4.不等式组的解集是( )
A.﹣2≤x≤3 B.x<﹣2,或x≥3 C.﹣2<x<3 D.﹣2<x≤3
5.如图,已知a∥b,∠1=80°,∠2=60°,则∠B的度数是( )
A.20° B.30° C.40° D.50°
6.已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )
A.(0,﹣4) B.(0,﹣8) C.(﹣4,0) D.(6,0)
7.已知关于x的不等式(1﹣a)x>2的解集为x<,则a的取值范围是( )
A.a>0 B.a>1 C.a<0 D.a<1
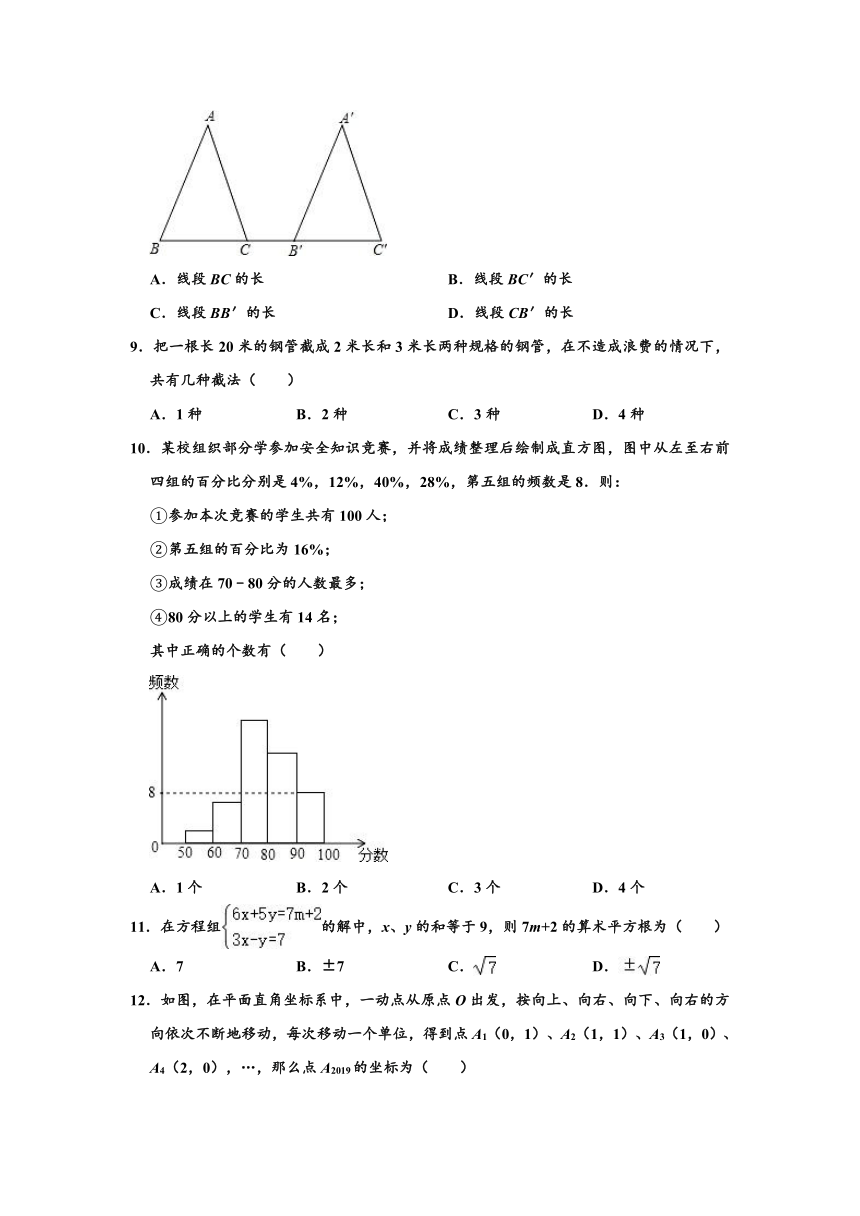
8.如图所示,△ABC沿BC平移后得到△A′B′C′,则△ABC移动的距离是( )
A.线段BC的长 B.线段BC′的长
C.线段BB′的长 D.线段CB′的长
9.把一根长20米的钢管截成2米长和3米长两种规格的钢管,在不造成浪费的情况下,共有几种截法( )
A.1种 B.2种 C.3种 D.4种
10.某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:
①参加本次竞赛的学生共有100人;
②第五组的百分比为16%;
③成绩在70﹣80分的人数最多;
④80分以上的学生有14名;
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
11.在方程组的解中,x、y的和等于9,则7m+2的算术平方根为( )
A.7 B.±7 C. D.
12.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2019的坐标为( )
A.(1008,1) B.(1009,1) C.(1009,0) D.(1010,0)
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题4分.
13.如图,数轴上所表示的不等式组的解集是: .
14.如果一个数的平方根为a+1和2a﹣7,则这个数为 .
15.如果实数x,y满足方程组,那么(﹣x+2y)2020= .
16.如果点A(2,n)在x轴上,那么点B(n﹣2,n+1)在第 象限.
17.如图,有下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BAD=180°.其中能得到AB∥CD的是 (填写编号).
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC,分别交AB、AC于点E、F.若AB=5,AC=4,那么△AEF的周长为 .
三、解答题:本大题共7小题,共78分.
19.计算:
(1);
(2)(+1)+|﹣2|.
20.解下列二元一次方程组、不等式组.
(1);
(2).
21.△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出△A′B′C′各点的坐标:A′ ;B′ C′ ;
(2)若点P(a,b)是△A′B′C′内部一点,则其图形变换后的对应点P′的坐标为 ;
(3)说明△A′B′C′是由△ABC经过怎样的图形变换得到的? ;
(4)△ABC的面积= .
22.学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如图不完整统计图表,请根据图表中的信息解答下列问题.
(1)直接写出a= ;b= ,c= ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?
组别 次数 频数(人) 百分比
1 60≤x<90 5 10%
2 90≤x<120 5 b
3 120≤x<150 18 36%
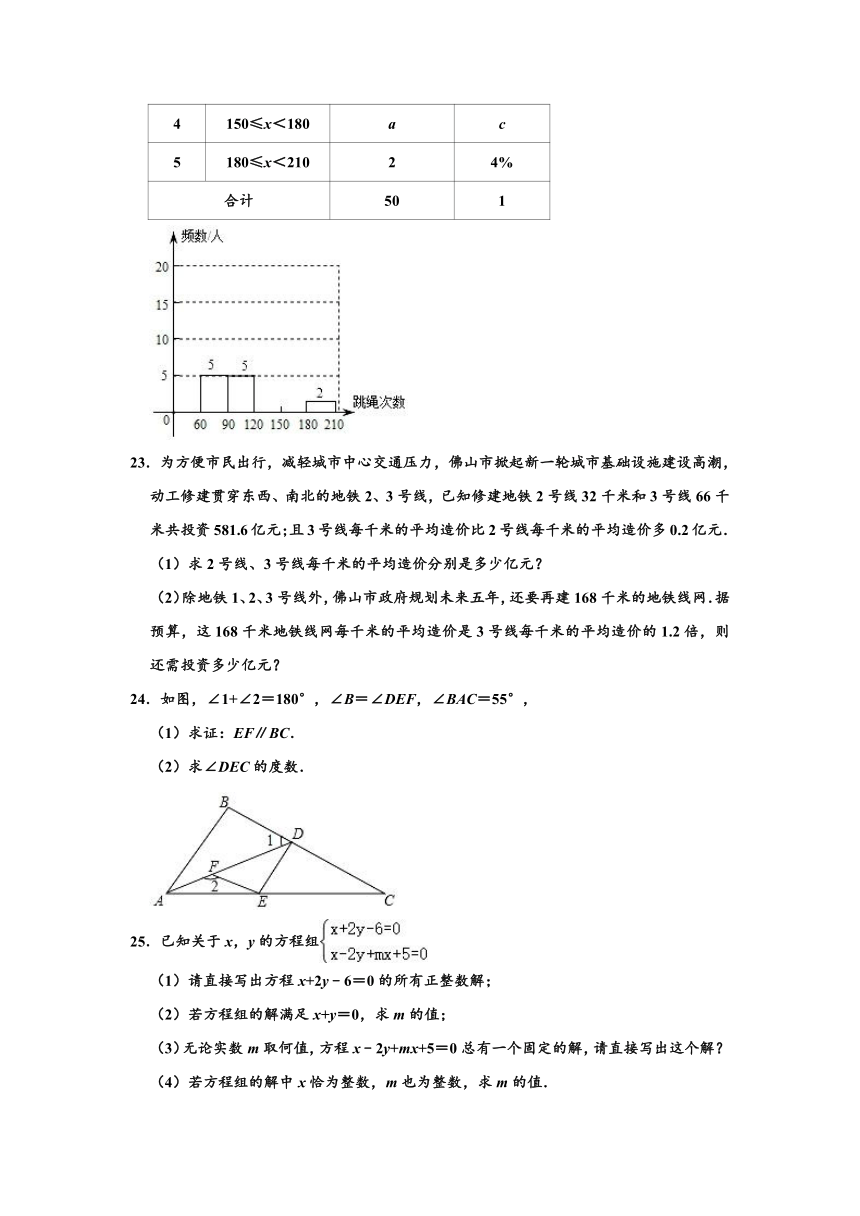
4 150≤x<180 a c
5 180≤x<210 2 4%
合计 50 1
23.为方便市民出行,减轻城市中心交通压力,佛山市掀起新一轮城市基础设施建设高潮,动工修建贯穿东西、南北的地铁2、3号线,已知修建地铁2号线32千米和3号线66千米共投资581.6亿元;且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元.
(1)求2号线、3号线每千米的平均造价分别是多少亿元?
(2)除地铁1、2、3号线外,佛山市政府规划未来五年,还要再建168千米的地铁线网.据预算,这168千米地铁线网每千米的平均造价是3号线每千米的平均造价的1.2倍,则还需投资多少亿元?
24.如图,∠1+∠2=180°,∠B=∠DEF,∠BAC=55°,
(1)求证:EF∥BC.
(2)求∠DEC的度数.
25.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
参考答案
一、选择题:本大题共12小题,每小题选对得4分,共48分.
1.9的算术平方根是( )
A.±3 B.3 C.﹣3 D.
解:9的算术平方根是3.
故选:B.
2.实数、、、﹣π、0、0.101001…中,无理数个数为( )
A.1 B.2 C.3 D.4
解:,,0,是整数,属于有理数;
无理数有:,﹣π,0.101001…共3个.
故选:C.
3.下列调查中,适宜采用普查方式的是( )
A.调查“奔跑吧,兄弟”节目的收视率
B.调查沧州市民对武术的喜爱
C.调查河北省七年级学生的身高
D.调查我国探月工程“嫦娥四号”的零部件质量
解:A.调查“奔跑吧,兄弟”节目的收视率,所费人力、物力和时间较多,适合选择抽样调查,故本选项不符合题意;
B.调查沧州市民对武术的喜爱,所费人力、物力和时间较多,适合选择抽样调查,故本选项不符合题意;
C.调查河北省七年级学生的身高,所费人力、物力和时间较多,适合选择抽样调查,故本选项不符合题意;
D.调查我国探月工程“嫦娥四号”的零部件质量,是精确度要求高的调查,适合普查,故本选项符合题意.
本选项故选:D.
4.不等式组的解集是( )
A.﹣2≤x≤3 B.x<﹣2,或x≥3 C.﹣2<x<3 D.﹣2<x≤3
解:解不等式①,得:x>﹣2,
解不等式②,得:x≤3,
所以不等式组的解集是:﹣2<x≤3.
故选:D.
5.如图,已知a∥b,∠1=80°,∠2=60°,则∠B的度数是( )
A.20° B.30° C.40° D.50°
解:∵a∥b,
∴∠1=∠3=80°,
∵∠2=60°,
∴∠B=180°﹣80°﹣60°=40°,
故选:C.
6.已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )
A.(0,﹣4) B.(0,﹣8) C.(﹣4,0) D.(6,0)
解:∵A(1,0),B(0,2),点P在x轴上,
∴AP边上的高为2,
又△PAB的面积为5,
∴AP=5,
而点P在x轴的负半轴上,
∴P(﹣4,0).
故选:C.
7.已知关于x的不等式(1﹣a)x>2的解集为x<,则a的取值范围是( )
A.a>0 B.a>1 C.a<0 D.a<1
解:∵不等式(1﹣a)x>2的解集为x<,
又∵不等号方向改变了,
∴1﹣a<0,
∴a>1;
故选:B.
8.如图所示,△ABC沿BC平移后得到△A′B′C′,则△ABC移动的距离是( )
A.线段BC的长 B.线段BC′的长
C.线段BB′的长 D.线段CB′的长
解:∵△ABC沿BC平移后得到△A′B′C′,
∴△ABC移动的距离是BB′.
故选:C.
9.把一根长20米的钢管截成2米长和3米长两种规格的钢管,在不造成浪费的情况下,共有几种截法( )
A.1种 B.2种 C.3种 D.4种
解:设截成2米长的钢管x段,3米长的钢管y段,
依题意,得:2x+3y=20,
∴x=10﹣y.
又∵x,y均为正整数,
∴,,,
∴共有3种截法.
故选:C.
10.某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:
①参加本次竞赛的学生共有100人;
②第五组的百分比为16%;
③成绩在70﹣80分的人数最多;
④80分以上的学生有14名;
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
解:①参加本次竞赛的学生共有8÷(1﹣4%﹣12%﹣40%﹣28%)=50(人),此项错误;
②第五组的百分比为1﹣4%﹣12%﹣40%﹣28%=16%,此项正确;
③成绩在70﹣80分的人数最多,此项正确;
④80分以上的学生有50×(28%+16%)=22(名),此项错误;
故选:B.
11.在方程组的解中,x、y的和等于9,则7m+2的算术平方根为( )
A.7 B.±7 C. D.
解:由题意知x、y满足,
①+②,得:4x=16,
解得x=4,
将x=4代入②,得:4+y=9,
解得y=5,
将x=4、y=5代入6x+5y=7m+2,得:7m+2=49,
∴7m+2即49的算术平方根为7,
故选:A.
12.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2019的坐标为( )
A.(1008,1) B.(1009,1) C.(1009,0) D.(1010,0)
解:根据题意和图的坐标可知:每次都移动一个单位长度,中按向上、向右、向下、向右的方向依次不断地移动A1(0,1)、A2(1,1)、A3(1,0)、
A4(2,0),A5(2,1)、A6(3,1)、A7(3,0)…
∴坐标变体的规律:每移动4次,它的纵坐标都为1,而横坐标向右移动了2个单位长度,也就是移动次数的一半;
∴2019÷4=504…3
∴A2019纵坐标是A3的纵坐标0;∴A2019横坐标是0+2×504+1=1009
那么点A2019的坐标为(1009,0)
故选:C.
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题4分.
13.如图,数轴上所表示的不等式组的解集是: ﹣2<x≤1 .
解:由图示可看出,从﹣2出发向右画出的线且﹣2处是空心圆,表示x>﹣2;
从1出发向左画出的线且1处是实心圆,表示x≤1,不等式组的解集是指它们的公共部分.
所以这个不等式组的解集是﹣2<x≤1.
14.如果一个数的平方根为a+1和2a﹣7,则这个数为 9 .
解:由题意得a+1=﹣(2a﹣7),
解得:a=2,
∴这个正数为:(3)2=9.
故答案为:9.
15.如果实数x,y满足方程组,那么(﹣x+2y)2020= 1 .
解:,
①+②得:3x=3,
解得:x=1,
把x=1代入②得:y=1,
则原式=(﹣1+2)2020=1.
故答案为:1
16.如果点A(2,n)在x轴上,那么点B(n﹣2,n+1)在第 二 象限.
解:因为点A(2,n)在x轴上,
所以n=0,
则点B为(﹣2,1),
所以点B在第二象限.
故答案为:二.
17.如图,有下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BAD=180°.其中能得到AB∥CD的是 ②③ (填写编号).
解:①∵∠1=∠2,
∴AD∥BC;
②∵∠3=∠4,
∴AB∥CD;
③∵∠B=∠5,
∴AB∥DC;
④∵∠B+∠BAD=180°,
∴AD∥BC,
∴能够得到AB∥CD的条件是②③,
故答案为:②③.
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC,分别交AB、AC于点E、F.若AB=5,AC=4,那么△AEF的周长为 9 .
解:由∠ABC与∠ACB的平分线相交于点O,得
∠EBO=∠OBC,∠FCO=∠OCB.
由EF∥BC,得
∠EOB=∠BOC,∠FOC=∠OCB,
∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=BE,OF=FC.
C△AEF=AE+EF+AF=AE+BE+AF+CF=AB+AC=9.
故答案为:9.
三、解答题:本大题共7小题,共78分.
19.计算:
(1);
(2)(+1)+|﹣2|.
解:(1)原式=5+1
=6;
(2)原式=3++2﹣
=5.
20.解下列二元一次方程组、不等式组.
(1);
(2).
解:(1)整理为:
,
①×5+②得,26x=208,
解得,x=8,
把x=8代入②得,8+5y=28,
解得,y=4,
所以,方程组的解为;
(2),
解不等式x﹣3(x﹣1)≥5得,x≤﹣1;
解不等式得,x≥﹣7,
所以,不等式组的解集为:﹣7≤x≤﹣1.
21.△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出△A′B′C′各点的坐标:A′ (﹣3,3) ;B′ (﹣2,﹣2) C′ (﹣1,﹣1) ;
(2)若点P(a,b)是△A′B′C′内部一点,则其图形变换后的对应点P′的坐标为 (a﹣4,b﹣2) ;
(3)说明△A′B′C′是由△ABC经过怎样的图形变换得到的? △ABC向左平移4个单位向下平移2个单位得到△A′B′C′ ;
(4)△ABC的面积= 2 .
解:(1)观察图象可知A′(﹣3,1),B′(﹣2,﹣2),C′(﹣1,﹣1),
故答案为(﹣3,1),(﹣2,﹣2),(﹣1,﹣1).
(2)点P向左平移4个单位向下平移2个单位得到P′,
∴P′(a﹣4,b﹣2).
故答案为(a﹣4,b﹣2).
(3)△ABC向左平移4个单位向下平移2个单位得到△A′B′C′,
故答案为:△ABC向左平移4个单位向下平移2个单位得到△A′B′C′.
(4)S△ABC=2×3﹣×1×3﹣×2×2﹣×1×1=2.
故答案为2.
22.学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如图不完整统计图表,请根据图表中的信息解答下列问题.
(1)直接写出a= 20 ;b= 10% ,c= 40% ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?
组别 次数 频数(人) 百分比
1 60≤x<90 5 10%
2 90≤x<120 5 b
3 120≤x<150 18 36%
4 150≤x<180 a c
5 180≤x<210 2 4%
合计 50 1
解:(1)a=50﹣5﹣5﹣18﹣2=20,
b=5÷50×100%=10%,
c=20÷50×100%=40%,
故答案为:20,10%,40%;
(2)由(1)知,a=20,
由频数分布表可知,第3组的频数为18,
补全的频数分布直方图如右图所示;
(3)400×(10%+36%)=184(人),
即该校七年级学生跳绳次数在90≤x<150范围的学生约有184人.
23.为方便市民出行,减轻城市中心交通压力,佛山市掀起新一轮城市基础设施建设高潮,动工修建贯穿东西、南北的地铁2、3号线,已知修建地铁2号线32千米和3号线66千米共投资581.6亿元;且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元.
(1)求2号线、3号线每千米的平均造价分别是多少亿元?
(2)除地铁1、2、3号线外,佛山市政府规划未来五年,还要再建168千米的地铁线网.据预算,这168千米地铁线网每千米的平均造价是3号线每千米的平均造价的1.2倍,则还需投资多少亿元?
解:(1)设2号线每千米的平均造价是x亿元,3号线每千米的平均造价是y亿元,
由题意得出:,
解得:,
答:2号线每千米的平均造价是5.8亿元,3号线每千米的平均造价是6亿元;
(2)由(1)得出:
168×6×1.2=1209.6(亿元),
答:还需投资1209.6亿元.
24.如图,∠1+∠2=180°,∠B=∠DEF,∠BAC=55°,
(1)求证:EF∥BC.
(2)求∠DEC的度数.
解:(1)证明:∵∠1+∠2=180°,∠DFE+∠2=180°,
∴∠1=∠DFE,
∴EF∥BC.
(2)∵EF∥BC,
∴∠DEF+∠BDE=180°
∵∠B=∠DEF,
∴∠B+∠BDE=180°,
∴AB∥DE,
∴∠DEC=∠BAC=55°,
答:∠DEC的度数为55°.
25.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
解:(1)方程x+2y﹣6=0,2x+y=6,
解得:y=6﹣2x,
当y=1时,x=4;当y=2时,x=2,
方程x+2y﹣6=0的所有正整数解为:,;
(2)由题意得:,解得,
把代入x﹣2y+mx+5=0,解得m=﹣;
(3)x﹣2y+mx+5=0,
(1+m)x﹣2y=﹣5,
∴当x=0时,y=2.5,
即固定的解为:,
(4),
①+②得:2x﹣6+mx+5=0,
(2+m)x=1,
x=,
∵x恰为整数,m也为整数,
∴2+m是1的约数,
2+m=1或﹣1,
m=﹣1或﹣3.
一、选择题(共12小题).
1.9的算术平方根是( )
A.±3 B.3 C.﹣3 D.
2.实数、、、﹣π、0、0.101001…中,无理数个数为( )
A.1 B.2 C.3 D.4
3.下列调查中,适宜采用普查方式的是( )
A.调查“奔跑吧,兄弟”节目的收视率
B.调查沧州市民对武术的喜爱
C.调查河北省七年级学生的身高
D.调查我国探月工程“嫦娥四号”的零部件质量
4.不等式组的解集是( )
A.﹣2≤x≤3 B.x<﹣2,或x≥3 C.﹣2<x<3 D.﹣2<x≤3
5.如图,已知a∥b,∠1=80°,∠2=60°,则∠B的度数是( )
A.20° B.30° C.40° D.50°
6.已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )
A.(0,﹣4) B.(0,﹣8) C.(﹣4,0) D.(6,0)
7.已知关于x的不等式(1﹣a)x>2的解集为x<,则a的取值范围是( )
A.a>0 B.a>1 C.a<0 D.a<1
8.如图所示,△ABC沿BC平移后得到△A′B′C′,则△ABC移动的距离是( )
A.线段BC的长 B.线段BC′的长
C.线段BB′的长 D.线段CB′的长
9.把一根长20米的钢管截成2米长和3米长两种规格的钢管,在不造成浪费的情况下,共有几种截法( )
A.1种 B.2种 C.3种 D.4种
10.某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:
①参加本次竞赛的学生共有100人;
②第五组的百分比为16%;
③成绩在70﹣80分的人数最多;
④80分以上的学生有14名;
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
11.在方程组的解中,x、y的和等于9,则7m+2的算术平方根为( )
A.7 B.±7 C. D.
12.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2019的坐标为( )
A.(1008,1) B.(1009,1) C.(1009,0) D.(1010,0)
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题4分.
13.如图,数轴上所表示的不等式组的解集是: .
14.如果一个数的平方根为a+1和2a﹣7,则这个数为 .
15.如果实数x,y满足方程组,那么(﹣x+2y)2020= .
16.如果点A(2,n)在x轴上,那么点B(n﹣2,n+1)在第 象限.
17.如图,有下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BAD=180°.其中能得到AB∥CD的是 (填写编号).
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC,分别交AB、AC于点E、F.若AB=5,AC=4,那么△AEF的周长为 .
三、解答题:本大题共7小题,共78分.
19.计算:
(1);
(2)(+1)+|﹣2|.
20.解下列二元一次方程组、不等式组.
(1);
(2).
21.△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出△A′B′C′各点的坐标:A′ ;B′ C′ ;
(2)若点P(a,b)是△A′B′C′内部一点,则其图形变换后的对应点P′的坐标为 ;
(3)说明△A′B′C′是由△ABC经过怎样的图形变换得到的? ;
(4)△ABC的面积= .
22.学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如图不完整统计图表,请根据图表中的信息解答下列问题.
(1)直接写出a= ;b= ,c= ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?
组别 次数 频数(人) 百分比
1 60≤x<90 5 10%
2 90≤x<120 5 b
3 120≤x<150 18 36%
4 150≤x<180 a c
5 180≤x<210 2 4%
合计 50 1
23.为方便市民出行,减轻城市中心交通压力,佛山市掀起新一轮城市基础设施建设高潮,动工修建贯穿东西、南北的地铁2、3号线,已知修建地铁2号线32千米和3号线66千米共投资581.6亿元;且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元.
(1)求2号线、3号线每千米的平均造价分别是多少亿元?
(2)除地铁1、2、3号线外,佛山市政府规划未来五年,还要再建168千米的地铁线网.据预算,这168千米地铁线网每千米的平均造价是3号线每千米的平均造价的1.2倍,则还需投资多少亿元?
24.如图,∠1+∠2=180°,∠B=∠DEF,∠BAC=55°,
(1)求证:EF∥BC.
(2)求∠DEC的度数.
25.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
参考答案
一、选择题:本大题共12小题,每小题选对得4分,共48分.
1.9的算术平方根是( )
A.±3 B.3 C.﹣3 D.
解:9的算术平方根是3.
故选:B.
2.实数、、、﹣π、0、0.101001…中,无理数个数为( )
A.1 B.2 C.3 D.4
解:,,0,是整数,属于有理数;
无理数有:,﹣π,0.101001…共3个.
故选:C.
3.下列调查中,适宜采用普查方式的是( )
A.调查“奔跑吧,兄弟”节目的收视率
B.调查沧州市民对武术的喜爱
C.调查河北省七年级学生的身高
D.调查我国探月工程“嫦娥四号”的零部件质量
解:A.调查“奔跑吧,兄弟”节目的收视率,所费人力、物力和时间较多,适合选择抽样调查,故本选项不符合题意;
B.调查沧州市民对武术的喜爱,所费人力、物力和时间较多,适合选择抽样调查,故本选项不符合题意;
C.调查河北省七年级学生的身高,所费人力、物力和时间较多,适合选择抽样调查,故本选项不符合题意;
D.调查我国探月工程“嫦娥四号”的零部件质量,是精确度要求高的调查,适合普查,故本选项符合题意.
本选项故选:D.
4.不等式组的解集是( )
A.﹣2≤x≤3 B.x<﹣2,或x≥3 C.﹣2<x<3 D.﹣2<x≤3
解:解不等式①,得:x>﹣2,
解不等式②,得:x≤3,
所以不等式组的解集是:﹣2<x≤3.
故选:D.
5.如图,已知a∥b,∠1=80°,∠2=60°,则∠B的度数是( )
A.20° B.30° C.40° D.50°
解:∵a∥b,
∴∠1=∠3=80°,
∵∠2=60°,
∴∠B=180°﹣80°﹣60°=40°,
故选:C.
6.已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )
A.(0,﹣4) B.(0,﹣8) C.(﹣4,0) D.(6,0)
解:∵A(1,0),B(0,2),点P在x轴上,
∴AP边上的高为2,
又△PAB的面积为5,
∴AP=5,
而点P在x轴的负半轴上,
∴P(﹣4,0).
故选:C.
7.已知关于x的不等式(1﹣a)x>2的解集为x<,则a的取值范围是( )
A.a>0 B.a>1 C.a<0 D.a<1
解:∵不等式(1﹣a)x>2的解集为x<,
又∵不等号方向改变了,
∴1﹣a<0,
∴a>1;
故选:B.
8.如图所示,△ABC沿BC平移后得到△A′B′C′,则△ABC移动的距离是( )
A.线段BC的长 B.线段BC′的长
C.线段BB′的长 D.线段CB′的长
解:∵△ABC沿BC平移后得到△A′B′C′,
∴△ABC移动的距离是BB′.
故选:C.
9.把一根长20米的钢管截成2米长和3米长两种规格的钢管,在不造成浪费的情况下,共有几种截法( )
A.1种 B.2种 C.3种 D.4种
解:设截成2米长的钢管x段,3米长的钢管y段,
依题意,得:2x+3y=20,
∴x=10﹣y.
又∵x,y均为正整数,
∴,,,
∴共有3种截法.
故选:C.
10.某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:
①参加本次竞赛的学生共有100人;
②第五组的百分比为16%;
③成绩在70﹣80分的人数最多;
④80分以上的学生有14名;
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
解:①参加本次竞赛的学生共有8÷(1﹣4%﹣12%﹣40%﹣28%)=50(人),此项错误;
②第五组的百分比为1﹣4%﹣12%﹣40%﹣28%=16%,此项正确;
③成绩在70﹣80分的人数最多,此项正确;
④80分以上的学生有50×(28%+16%)=22(名),此项错误;
故选:B.
11.在方程组的解中,x、y的和等于9,则7m+2的算术平方根为( )
A.7 B.±7 C. D.
解:由题意知x、y满足,
①+②,得:4x=16,
解得x=4,
将x=4代入②,得:4+y=9,
解得y=5,
将x=4、y=5代入6x+5y=7m+2,得:7m+2=49,
∴7m+2即49的算术平方根为7,
故选:A.
12.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2019的坐标为( )
A.(1008,1) B.(1009,1) C.(1009,0) D.(1010,0)
解:根据题意和图的坐标可知:每次都移动一个单位长度,中按向上、向右、向下、向右的方向依次不断地移动A1(0,1)、A2(1,1)、A3(1,0)、
A4(2,0),A5(2,1)、A6(3,1)、A7(3,0)…
∴坐标变体的规律:每移动4次,它的纵坐标都为1,而横坐标向右移动了2个单位长度,也就是移动次数的一半;
∴2019÷4=504…3
∴A2019纵坐标是A3的纵坐标0;∴A2019横坐标是0+2×504+1=1009
那么点A2019的坐标为(1009,0)
故选:C.
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题4分.
13.如图,数轴上所表示的不等式组的解集是: ﹣2<x≤1 .
解:由图示可看出,从﹣2出发向右画出的线且﹣2处是空心圆,表示x>﹣2;
从1出发向左画出的线且1处是实心圆,表示x≤1,不等式组的解集是指它们的公共部分.
所以这个不等式组的解集是﹣2<x≤1.
14.如果一个数的平方根为a+1和2a﹣7,则这个数为 9 .
解:由题意得a+1=﹣(2a﹣7),
解得:a=2,
∴这个正数为:(3)2=9.
故答案为:9.
15.如果实数x,y满足方程组,那么(﹣x+2y)2020= 1 .
解:,
①+②得:3x=3,
解得:x=1,
把x=1代入②得:y=1,
则原式=(﹣1+2)2020=1.
故答案为:1
16.如果点A(2,n)在x轴上,那么点B(n﹣2,n+1)在第 二 象限.
解:因为点A(2,n)在x轴上,
所以n=0,
则点B为(﹣2,1),
所以点B在第二象限.
故答案为:二.
17.如图,有下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BAD=180°.其中能得到AB∥CD的是 ②③ (填写编号).
解:①∵∠1=∠2,
∴AD∥BC;
②∵∠3=∠4,
∴AB∥CD;
③∵∠B=∠5,
∴AB∥DC;
④∵∠B+∠BAD=180°,
∴AD∥BC,
∴能够得到AB∥CD的条件是②③,
故答案为:②③.
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC,分别交AB、AC于点E、F.若AB=5,AC=4,那么△AEF的周长为 9 .
解:由∠ABC与∠ACB的平分线相交于点O,得
∠EBO=∠OBC,∠FCO=∠OCB.
由EF∥BC,得
∠EOB=∠BOC,∠FOC=∠OCB,
∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=BE,OF=FC.
C△AEF=AE+EF+AF=AE+BE+AF+CF=AB+AC=9.
故答案为:9.
三、解答题:本大题共7小题,共78分.
19.计算:
(1);
(2)(+1)+|﹣2|.
解:(1)原式=5+1
=6;
(2)原式=3++2﹣
=5.
20.解下列二元一次方程组、不等式组.
(1);
(2).
解:(1)整理为:
,
①×5+②得,26x=208,
解得,x=8,
把x=8代入②得,8+5y=28,
解得,y=4,
所以,方程组的解为;
(2),
解不等式x﹣3(x﹣1)≥5得,x≤﹣1;
解不等式得,x≥﹣7,
所以,不等式组的解集为:﹣7≤x≤﹣1.
21.△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出△A′B′C′各点的坐标:A′ (﹣3,3) ;B′ (﹣2,﹣2) C′ (﹣1,﹣1) ;
(2)若点P(a,b)是△A′B′C′内部一点,则其图形变换后的对应点P′的坐标为 (a﹣4,b﹣2) ;
(3)说明△A′B′C′是由△ABC经过怎样的图形变换得到的? △ABC向左平移4个单位向下平移2个单位得到△A′B′C′ ;
(4)△ABC的面积= 2 .
解:(1)观察图象可知A′(﹣3,1),B′(﹣2,﹣2),C′(﹣1,﹣1),
故答案为(﹣3,1),(﹣2,﹣2),(﹣1,﹣1).
(2)点P向左平移4个单位向下平移2个单位得到P′,
∴P′(a﹣4,b﹣2).
故答案为(a﹣4,b﹣2).
(3)△ABC向左平移4个单位向下平移2个单位得到△A′B′C′,
故答案为:△ABC向左平移4个单位向下平移2个单位得到△A′B′C′.
(4)S△ABC=2×3﹣×1×3﹣×2×2﹣×1×1=2.
故答案为2.
22.学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如图不完整统计图表,请根据图表中的信息解答下列问题.
(1)直接写出a= 20 ;b= 10% ,c= 40% ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?
组别 次数 频数(人) 百分比
1 60≤x<90 5 10%
2 90≤x<120 5 b
3 120≤x<150 18 36%
4 150≤x<180 a c
5 180≤x<210 2 4%
合计 50 1
解:(1)a=50﹣5﹣5﹣18﹣2=20,
b=5÷50×100%=10%,
c=20÷50×100%=40%,
故答案为:20,10%,40%;
(2)由(1)知,a=20,
由频数分布表可知,第3组的频数为18,
补全的频数分布直方图如右图所示;
(3)400×(10%+36%)=184(人),
即该校七年级学生跳绳次数在90≤x<150范围的学生约有184人.
23.为方便市民出行,减轻城市中心交通压力,佛山市掀起新一轮城市基础设施建设高潮,动工修建贯穿东西、南北的地铁2、3号线,已知修建地铁2号线32千米和3号线66千米共投资581.6亿元;且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元.
(1)求2号线、3号线每千米的平均造价分别是多少亿元?
(2)除地铁1、2、3号线外,佛山市政府规划未来五年,还要再建168千米的地铁线网.据预算,这168千米地铁线网每千米的平均造价是3号线每千米的平均造价的1.2倍,则还需投资多少亿元?
解:(1)设2号线每千米的平均造价是x亿元,3号线每千米的平均造价是y亿元,
由题意得出:,
解得:,
答:2号线每千米的平均造价是5.8亿元,3号线每千米的平均造价是6亿元;
(2)由(1)得出:
168×6×1.2=1209.6(亿元),
答:还需投资1209.6亿元.
24.如图,∠1+∠2=180°,∠B=∠DEF,∠BAC=55°,
(1)求证:EF∥BC.
(2)求∠DEC的度数.
解:(1)证明:∵∠1+∠2=180°,∠DFE+∠2=180°,
∴∠1=∠DFE,
∴EF∥BC.
(2)∵EF∥BC,
∴∠DEF+∠BDE=180°
∵∠B=∠DEF,
∴∠B+∠BDE=180°,
∴AB∥DE,
∴∠DEC=∠BAC=55°,
答:∠DEC的度数为55°.
25.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
解:(1)方程x+2y﹣6=0,2x+y=6,
解得:y=6﹣2x,
当y=1时,x=4;当y=2时,x=2,
方程x+2y﹣6=0的所有正整数解为:,;
(2)由题意得:,解得,
把代入x﹣2y+mx+5=0,解得m=﹣;
(3)x﹣2y+mx+5=0,
(1+m)x﹣2y=﹣5,
∴当x=0时,y=2.5,
即固定的解为:,
(4),
①+②得:2x﹣6+mx+5=0,
(2+m)x=1,
x=,
∵x恰为整数,m也为整数,
∴2+m是1的约数,
2+m=1或﹣1,
m=﹣1或﹣3.
同课章节目录
