2019-2020学年广东省河源市高二下学期期末数学试卷 (Word解析版)
文档属性
| 名称 | 2019-2020学年广东省河源市高二下学期期末数学试卷 (Word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1020.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 21:19:58 | ||
图片预览




文档简介
2019-2020学年广东省河源市高二第二学期期末数学试卷
一、选择题(共12小题).
1.已知全集U={x∈Z|0≤x≤4},集合A={1,2,3,4},B={0,2,4},则?U(A∩B)=( )
A.{1,3} B.{0,1,3} C.{0,4} D.{0,1,2,3,4}
2.若(2﹣mi)(3﹣2i)(m∈R)是纯虚数,则m=( )
A.0 B.1 C.2 D.3
3.已知a=lg2,b=ln2,c=e,则( )
A.a<b<c B.a<c<b C.b<c<a D.b<a<c
4.已知直线m,n和平面α,且n?α,那么“m∥α”是“m∥n”( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.(1﹣x)4的展开式中x3的系数为( )
A.﹣8 B.8 C.﹣16 D.16
6.已知数列{an}为等比数列,若a3=1,a9=125,则a5=( )
A.±5 B.25 C. D.5
7.港珠澳大桥位于中国广东省珠江口伶仃洋海域内,是中国境内一项连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度和顶尖的建造技术而闻名世界.2018年10月24日上午9时开通运营后香港到澳门之间4个小时的陆路车程极大缩短.为了解实际通行所需时间,随机抽取了n台车辆进行统计,结果显示这些车辆的通行时间(单位:分钟)都在[35,50]内,按通行时间分为[35,38),[38,41),[41,44),[44,47),[47,50]五组,其中通行时间在[38,47)的车辆有182台,频率分布直方图如图所示,则n=( )
A.280 B.260 C.250 D.200
8.已知函数f(x)=,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
A.﹣ B.﹣ C. D.
9.已知向量,满足||=3||,?=6,<,>=,则||=( )
A.2 B.3 C.4 D.6
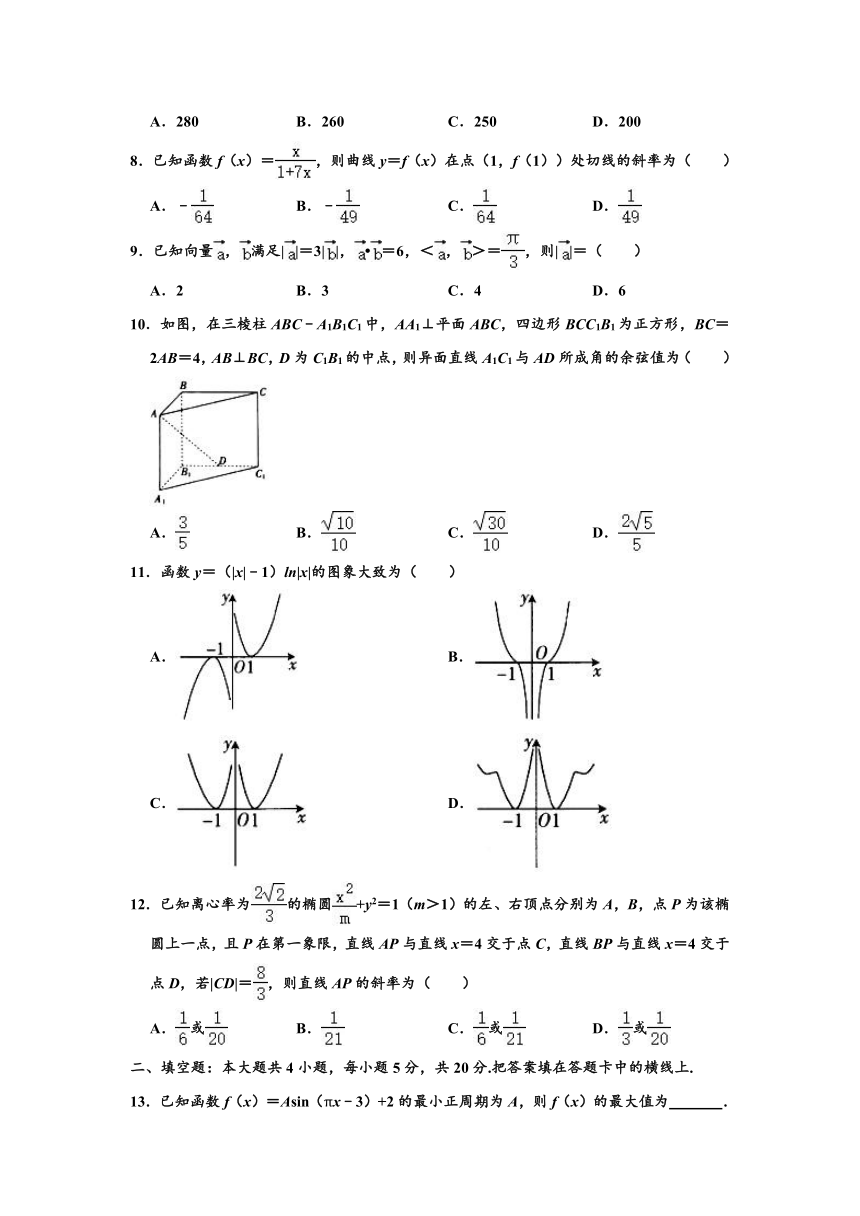
10.如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,D为C1B1的中点,则异面直线A1C1与AD所成角的余弦值为( )
A. B. C. D.
11.函数y=(|x|﹣1)ln|x|的图象大致为( )
A. B.
C. D.
12.已知离心率为的椭圆+y2=1(m>1)的左、右顶点分别为A,B,点P为该椭圆上一点,且P在第一象限,直线AP与直线x=4交于点C,直线BP与直线x=4交于点D,若|CD|=,则直线AP的斜率为( )
A.或 B. C.或 D.或
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知函数f(x)=Asin(πx﹣3)+2的最小正周期为A,则f(x)的最大值为 .
14.若双曲线C:x2﹣=1(b>0)的浙近线方程为y=±7x,则b= .
15.已知定义域为R的函数f(x)满足f(﹣x)=﹣f(x),f(x+2)=﹣f(x),且当0<x≤1时,f(x)=2x2﹣log8x,则f(47)= .
16.如图,将一个圆柱2n(n∈N*)等分切割,再重新组合成一个与圆柱等底等高的几何体,当n越大,重新组合的几何体就越接近于一个“长方体”,若新几何体的表面积比圆柱的表面积增加了8,则圆柱的侧面积为 ,在满足前面条件且圆柱外接球表面积最小时,它的外接球体积为 .
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤,考生根据要求作答,)
17.已知等差数列{an}的前n项和为Sn,且Sn=2n2+kn+k.
(1)求{an}的通项公式;
(2)若bn=,求数列{bn}的前n项和Tn.
18.在△ABC中,角A,B,C的对边分别为a,b,c,且=.
(1)若△ABC的外接圆半径为,求b;
(2)若b=4,a+c=6,求△ABC的面积.
19.在某公司举行的年会中,为了表彰年度优秀员工,该公司特意设置了二个抽奖环节,其规则如下,一个不透明的箱子中装有形状、大小相同的两个红色小球和四个绿色小球,从箱子中一次取出两个小球,同色奖励,不同色不奖励,一名优秀员工仅有一次抽奖机会若取出的两个均为红色,奖励2000元;若两个均为绿色,奖励1000元.
(1)求优秀员工小张获得2000元的概率;
(2)若一对夫妻均为年度优秀员工,求这对夫妻获得的奖励总金额X的分布列和数学期望.
20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,BC∥AD,AB⊥AD,E为侧棱PA上一点,且AE=2PE,AP=3,AB=BC=2,AD=4.
(1)证明:PC∥平面BDE.
(2)求平面PCD与平面BDE所成锐二面角的余弦值.
21.已知直线y=kx﹣3(k>1)与抛物线C;x2=﹣4y相交于A,B两点,且线段AB的中点为D(x0,y0).
(1)证明:y0<﹣5.
(2)过D作x轴的垂线,垂足为E,过E作直线AB的垂线,交C于M,N两点,求|MN|的取值范围.
22.已知函数f(x)=(x﹣m)ex﹣m.
(1)求f(x)的单调区间;
(2)若xlnx<e对x∈(1,+∞)恒成立,求a的取值范围.
参考答案
一、选择题(共12小题).
1.已知全集U={x∈Z|0≤x≤4},集合A={1,2,3,4},B={0,2,4},则?U(A∩B)=( )
A.{1,3} B.{0,1,3} C.{0,4} D.{0,1,2,3,4}
解:∵全集U={x∈Z|0≤x≤4}={0,1,2,3,4},
集合A={1,2,3,4},B={0,2,4},
∴A∩B={2,4},
∴?U(A∩B)={0,1,3}.
故选:B.
2.若(2﹣mi)(3﹣2i)(m∈R)是纯虚数,则m=( )
A.0 B.1 C.2 D.3
解:∵(2﹣mi)(3﹣2i)=(6﹣2m)﹣(3m+4)i是纯虚数,
∴,即m=3.
故选:D.
3.已知a=lg2,b=ln2,c=e,则( )
A.a<b<c B.a<c<b C.b<c<a D.b<a<c
解:∵0=lg1<a=lg2<b=ln2<lne=1,
c=e>e0=1,
∴a<b<c.
故选:A.
4.已知直线m,n和平面α,且n?α,那么“m∥α”是“m∥n”( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:直线m,n,平面α,n?α,
“m∥α”?“m与n平行或异面”,
“m∥n”?“m与α平行或m?α”,
∴“m∥α”是“m∥n”的既不充分也不必要条件.
故选:D.
5.(1﹣x)4的展开式中x3的系数为( )
A.﹣8 B.8 C.﹣16 D.16
解:展开式的通项公式为Tk+1=C(x)k,
令k=3,则T4=C(x)3=﹣8x3,
则x3的系数为﹣8,
故选:A.
6.已知数列{an}为等比数列,若a3=1,a9=125,则a5=( )
A.±5 B.25 C. D.5
解:设等比数列{an}的公比为q,∵a3=1,a9=125,
∴1×q6=125,解得q2=5.
∴a5==5.
故选:D.
7.港珠澳大桥位于中国广东省珠江口伶仃洋海域内,是中国境内一项连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度和顶尖的建造技术而闻名世界.2018年10月24日上午9时开通运营后香港到澳门之间4个小时的陆路车程极大缩短.为了解实际通行所需时间,随机抽取了n台车辆进行统计,结果显示这些车辆的通行时间(单位:分钟)都在[35,50]内,按通行时间分为[35,38),[38,41),[41,44),[44,47),[47,50]五组,其中通行时间在[38,47)的车辆有182台,频率分布直方图如图所示,则n=( )
A.280 B.260 C.250 D.200
解:由题意可知,通行时间在[38,47)的频率为1﹣(0.01+0.02)×3=0.91,
所以,解得n=200.
故选:D.
8.已知函数f(x)=,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
A.﹣ B.﹣ C. D.
解:函数f(x)=,f′(x)=,
故f′(1)=,
所以曲线y=f(x)在点(1,f(1))处的切线的斜率为.
故选:C.
9.已知向量,满足||=3||,?=6,<,>=,则||=( )
A.2 B.3 C.4 D.6
解:因为?=cos<,>=||?||?cos=6,所以||=6.
故选:D.
10.如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,D为C1B1的中点,则异面直线A1C1与AD所成角的余弦值为( )
A. B. C. D.
解:如图,过点D作DF∥A1C1,交A1B1于点F,
则∠ADF为异面直线A1C1与AD所成角(或所成角的补角),
∵在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,
四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,D为C1B1的中点,
∴由题意知AD==,DF==,AF==,
∴异面直线A1C1与AD所成角的余弦值为:
cos∠ADF===.
故选:C.
11.函数y=(|x|﹣1)ln|x|的图象大致为( )
A. B.
C. D.
解:根据题意,f(x)=(|x|﹣1)ln|x|,有f(﹣x)=(|x|﹣1)ln|x|=f(x),
即函数y=(|x|﹣1)ln|x|为偶函数,排除A选项;
当0<x<1时,ln|x|<0,|x|﹣1<0,所以y=(|x|﹣1)ln|x|>0,排除B选项;
当x>1时,y=(x﹣1)lnx,,所以函数y=(|x|﹣1)ln|x|在(1,+∞)上单调递增,排除D选项.
故选:C.
12.已知离心率为的椭圆+y2=1(m>1)的左、右顶点分别为A,B,点P为该椭圆上一点,且P在第一象限,直线AP与直线x=4交于点C,直线BP与直线x=4交于点D,若|CD|=,则直线AP的斜率为( )
A.或 B. C.或 D.或
解:由,得m=9.
设p(x0,y0),则.
设kPA=k(0<k<),则,直线AP的方程为y=k(x+3),则C的坐标(4,7k).
直线BP的方程为y=,则D坐标(4,).
所以|CD|=7k+,解得k=(舍去)或.
故选:B.
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知函数f(x)=Asin(πx﹣3)+2的最小正周期为A,则f(x)的最大值为 4 .
解:∵函数f(x)=Asin(πx﹣3)+2的最小正周期为A,
∴A==2,
∴f(x)=2sin(πx﹣3)+2的最大值为4.
故答案为:4.
14.若双曲线C:x2﹣=1(b>0)的浙近线方程为y=±7x,则b= 7 .
解:双曲线C:x2﹣=1(b>0)的浙近线方程为y=±7x,
可得b=7.
故答案为:7.
15.已知定义域为R的函数f(x)满足f(﹣x)=﹣f(x),f(x+2)=﹣f(x),且当0<x≤1时,f(x)=2x2﹣log8x,则f(47)= ﹣2 .
解:∵函数f(x)满足f(﹣x)=﹣f(x),∴函数是奇函数,
f(x+2)=﹣f(x)=﹣f(x),
所以f(x+4)=﹣f(x+2)=f(x),
所以函数的周期为4,
当0<x≤1时,f(x)=2x2﹣log8x,
则f(47)=f(12×4﹣1)=f(﹣1)=﹣f(1)
=﹣(2×12﹣log81)=﹣2.
故答案为:﹣2.
16.如图,将一个圆柱2n(n∈N*)等分切割,再重新组合成一个与圆柱等底等高的几何体,当n越大,重新组合的几何体就越接近于一个“长方体”,若新几何体的表面积比圆柱的表面积增加了8,则圆柱的侧面积为 8π ,在满足前面条件且圆柱外接球表面积最小时,它的外接球体积为 .
解:设圆柱的底面半径为r,高h,外接球半径R,则2rh=8即hr=4,
所以圆柱的侧面积为2πrh=8π,
R2=≥rh=4即R≥2,当且仅当r==2时取等号,
此时外接球的表面积最小V==.
故答案为:8π;.
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤,考生根据要求作答,)
17.已知等差数列{an}的前n项和为Sn,且Sn=2n2+kn+k.
(1)求{an}的通项公式;
(2)若bn=,求数列{bn}的前n项和Tn.
解:(1)由题意,设等差数列{an}的公差为d,则
Sn=n2+(a1﹣)n=2n2+kn+k.
故,解得.
∴数列{an}的通项公式为an=2+4(n﹣1)=4n﹣2.
(2)由(1)知,
bn===?(﹣).
故Tn=b1+b2+…+bn
=?(1﹣)+?(﹣)+…+?(﹣)
=?(1﹣+﹣+…+﹣)
=?(1﹣)
=.
18.在△ABC中,角A,B,C的对边分别为a,b,c,且=.
(1)若△ABC的外接圆半径为,求b;
(2)若b=4,a+c=6,求△ABC的面积.
解:(1)△ABC中,角A,B,C的对边分别为a,b,c,且===,
由正弦定理可得=,
∴cos=sinB=2sincos,
∵cos≠0,
∴sin=,
∴=或=,(舍去),
∴B=,
∵△ABC的外接圆半径为,
∴=2R=2,
∴b=2×=3,
(2)由余弦定理可得b2=a2+c2﹣2accosB=(a+c)2﹣3ac,
即16=36﹣3ac,
∴ac=,
∴S△ABC=acsinB=××=.
19.在某公司举行的年会中,为了表彰年度优秀员工,该公司特意设置了二个抽奖环节,其规则如下,一个不透明的箱子中装有形状、大小相同的两个红色小球和四个绿色小球,从箱子中一次取出两个小球,同色奖励,不同色不奖励,一名优秀员工仅有一次抽奖机会若取出的两个均为红色,奖励2000元;若两个均为绿色,奖励1000元.
(1)求优秀员工小张获得2000元的概率;
(2)若一对夫妻均为年度优秀员工,求这对夫妻获得的奖励总金额X的分布列和数学期望.
解:(1)记“小张获得2000元”为事件A,
取出两个小球共有=15种情况,
其中两个小球均为红色共有=1种情况,
∴优秀员工小张获得2000元的概率为p(A)=.
(2)记“一名员工中奖1000元”为事件B,“一名员工不中奖”为事件C,
则P(B)==,
P(C)=1﹣P(A)﹣P(B)=,
由题知X所有的可能取值为0,1000,2000,3000,4000,
则P(X=0)=P(C)P(C)==,
P(X=1000)=2P(B)P(C)=2×=,
P(X=2000)=2P(A)P(C)+P(B)P(B)=+=,
P(X=3000)=2P(A)P(B)=2×=,
P(X=4000)=P(A)P(A)=,
∴X的分布列为:
X 0 1000 2000 3000 4000
P
E(X)=+=.
20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,BC∥AD,AB⊥AD,E为侧棱PA上一点,且AE=2PE,AP=3,AB=BC=2,AD=4.
(1)证明:PC∥平面BDE.
(2)求平面PCD与平面BDE所成锐二面角的余弦值.
解:(1)证明:连结AC,交BD于点F,连结EF,
∵BC∥AD,∴△BFC∽△DFA,∴,
∵=2.∴,∴EF∥PC,
∵EF?平面BDE,PC?平面BDE,
∴PC∥平面BDE.
(2)解:以A为坐标原点,建立空间直角坐标系A﹣xyz,如图所示,
则B(2,0,0),D(0,4,0),C(2,2,0),P(0,0,3),E(0,0,2),
则=(﹣2,2,0),=(0,4,﹣3),=(﹣2,4,0),=(0,4,﹣2),
设平面PCD的法向量=(x,y,z),
则,取x=3,得=(3,3,4),
设平面BDE的法向量=(a,b,c),
则,取b=1,得=(2,1,2),
cos<>===.
∴平面PCD与平面BDE所成锐二面角的余弦值为.
21.已知直线y=kx﹣3(k>1)与抛物线C;x2=﹣4y相交于A,B两点,且线段AB的中点为D(x0,y0).
(1)证明:y0<﹣5.
(2)过D作x轴的垂线,垂足为E,过E作直线AB的垂线,交C于M,N两点,求|MN|的取值范围.
解:(1)证明:由,可得x2+4kx﹣12=0,
设A(x1,y1),B(x2,y2),则x1+x2=﹣4k,
可得x0==﹣2k,y0=kx0﹣3=﹣2k2﹣3,
因为k>1,所以y0<﹣5;
(2)由题意,可得E的坐标为(﹣2k,0),
直线MN的方程为y=﹣(x+2k)即y=﹣x﹣2,
由可,得x2﹣x﹣8=0,
设M(x3,y3),N(x4,y4),可得x3+x4=,x3x4=﹣8,
△=+32>0恒成立,
|MN|=?==4,
由k>1,所以0<<1,则2<++2<6,
故|MN|的取值范围是(4,4).
22.已知函数f(x)=(x﹣m)ex﹣m.
(1)求f(x)的单调区间;
(2)若xlnx<e对x∈(1,+∞)恒成立,求a的取值范围.
解:(1)由f(x)=(x﹣m)ex﹣m,得f′(x)=(x﹣m+1)ex﹣m.
令f′(x)<0,得x<m﹣1,令f′(x)>0,得x>m﹣1.
∴f(x)的单调减区间为(﹣∞,m﹣1),单调递增区间为(m﹣1,+∞);
(2)当m=0时,f(x)=xex,由(1)知,f(x)在(0,+∞)上单调递增.
xlnx<e对x∈(1,+∞)恒成立,
即elnx?lnx<e对x∈(1,+∞)恒成立,
当x∈(1,+∞)时,lnx>0,x2>0,
当a<0时,不等式elnx?lnx<e显然不成立.
故a>0.
∴>0,则lnx<,即a<.
设函数g(x)=(x>1),则g′(x)=(x>1).
当1<x<时,g′(x)<0,当x>时,g′(x)>0,
∴.
故0<a<2e.
即a的取值范围是(0,2e).
一、选择题(共12小题).
1.已知全集U={x∈Z|0≤x≤4},集合A={1,2,3,4},B={0,2,4},则?U(A∩B)=( )
A.{1,3} B.{0,1,3} C.{0,4} D.{0,1,2,3,4}
2.若(2﹣mi)(3﹣2i)(m∈R)是纯虚数,则m=( )
A.0 B.1 C.2 D.3
3.已知a=lg2,b=ln2,c=e,则( )
A.a<b<c B.a<c<b C.b<c<a D.b<a<c
4.已知直线m,n和平面α,且n?α,那么“m∥α”是“m∥n”( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.(1﹣x)4的展开式中x3的系数为( )
A.﹣8 B.8 C.﹣16 D.16
6.已知数列{an}为等比数列,若a3=1,a9=125,则a5=( )
A.±5 B.25 C. D.5
7.港珠澳大桥位于中国广东省珠江口伶仃洋海域内,是中国境内一项连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度和顶尖的建造技术而闻名世界.2018年10月24日上午9时开通运营后香港到澳门之间4个小时的陆路车程极大缩短.为了解实际通行所需时间,随机抽取了n台车辆进行统计,结果显示这些车辆的通行时间(单位:分钟)都在[35,50]内,按通行时间分为[35,38),[38,41),[41,44),[44,47),[47,50]五组,其中通行时间在[38,47)的车辆有182台,频率分布直方图如图所示,则n=( )
A.280 B.260 C.250 D.200
8.已知函数f(x)=,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
A.﹣ B.﹣ C. D.
9.已知向量,满足||=3||,?=6,<,>=,则||=( )
A.2 B.3 C.4 D.6
10.如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,D为C1B1的中点,则异面直线A1C1与AD所成角的余弦值为( )
A. B. C. D.
11.函数y=(|x|﹣1)ln|x|的图象大致为( )
A. B.
C. D.
12.已知离心率为的椭圆+y2=1(m>1)的左、右顶点分别为A,B,点P为该椭圆上一点,且P在第一象限,直线AP与直线x=4交于点C,直线BP与直线x=4交于点D,若|CD|=,则直线AP的斜率为( )
A.或 B. C.或 D.或
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知函数f(x)=Asin(πx﹣3)+2的最小正周期为A,则f(x)的最大值为 .
14.若双曲线C:x2﹣=1(b>0)的浙近线方程为y=±7x,则b= .
15.已知定义域为R的函数f(x)满足f(﹣x)=﹣f(x),f(x+2)=﹣f(x),且当0<x≤1时,f(x)=2x2﹣log8x,则f(47)= .
16.如图,将一个圆柱2n(n∈N*)等分切割,再重新组合成一个与圆柱等底等高的几何体,当n越大,重新组合的几何体就越接近于一个“长方体”,若新几何体的表面积比圆柱的表面积增加了8,则圆柱的侧面积为 ,在满足前面条件且圆柱外接球表面积最小时,它的外接球体积为 .
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤,考生根据要求作答,)
17.已知等差数列{an}的前n项和为Sn,且Sn=2n2+kn+k.
(1)求{an}的通项公式;
(2)若bn=,求数列{bn}的前n项和Tn.
18.在△ABC中,角A,B,C的对边分别为a,b,c,且=.
(1)若△ABC的外接圆半径为,求b;
(2)若b=4,a+c=6,求△ABC的面积.
19.在某公司举行的年会中,为了表彰年度优秀员工,该公司特意设置了二个抽奖环节,其规则如下,一个不透明的箱子中装有形状、大小相同的两个红色小球和四个绿色小球,从箱子中一次取出两个小球,同色奖励,不同色不奖励,一名优秀员工仅有一次抽奖机会若取出的两个均为红色,奖励2000元;若两个均为绿色,奖励1000元.
(1)求优秀员工小张获得2000元的概率;
(2)若一对夫妻均为年度优秀员工,求这对夫妻获得的奖励总金额X的分布列和数学期望.
20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,BC∥AD,AB⊥AD,E为侧棱PA上一点,且AE=2PE,AP=3,AB=BC=2,AD=4.
(1)证明:PC∥平面BDE.
(2)求平面PCD与平面BDE所成锐二面角的余弦值.
21.已知直线y=kx﹣3(k>1)与抛物线C;x2=﹣4y相交于A,B两点,且线段AB的中点为D(x0,y0).
(1)证明:y0<﹣5.
(2)过D作x轴的垂线,垂足为E,过E作直线AB的垂线,交C于M,N两点,求|MN|的取值范围.
22.已知函数f(x)=(x﹣m)ex﹣m.
(1)求f(x)的单调区间;
(2)若xlnx<e对x∈(1,+∞)恒成立,求a的取值范围.
参考答案
一、选择题(共12小题).
1.已知全集U={x∈Z|0≤x≤4},集合A={1,2,3,4},B={0,2,4},则?U(A∩B)=( )
A.{1,3} B.{0,1,3} C.{0,4} D.{0,1,2,3,4}
解:∵全集U={x∈Z|0≤x≤4}={0,1,2,3,4},
集合A={1,2,3,4},B={0,2,4},
∴A∩B={2,4},
∴?U(A∩B)={0,1,3}.
故选:B.
2.若(2﹣mi)(3﹣2i)(m∈R)是纯虚数,则m=( )
A.0 B.1 C.2 D.3
解:∵(2﹣mi)(3﹣2i)=(6﹣2m)﹣(3m+4)i是纯虚数,
∴,即m=3.
故选:D.
3.已知a=lg2,b=ln2,c=e,则( )
A.a<b<c B.a<c<b C.b<c<a D.b<a<c
解:∵0=lg1<a=lg2<b=ln2<lne=1,
c=e>e0=1,
∴a<b<c.
故选:A.
4.已知直线m,n和平面α,且n?α,那么“m∥α”是“m∥n”( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:直线m,n,平面α,n?α,
“m∥α”?“m与n平行或异面”,
“m∥n”?“m与α平行或m?α”,
∴“m∥α”是“m∥n”的既不充分也不必要条件.
故选:D.
5.(1﹣x)4的展开式中x3的系数为( )
A.﹣8 B.8 C.﹣16 D.16
解:展开式的通项公式为Tk+1=C(x)k,
令k=3,则T4=C(x)3=﹣8x3,
则x3的系数为﹣8,
故选:A.
6.已知数列{an}为等比数列,若a3=1,a9=125,则a5=( )
A.±5 B.25 C. D.5
解:设等比数列{an}的公比为q,∵a3=1,a9=125,
∴1×q6=125,解得q2=5.
∴a5==5.
故选:D.
7.港珠澳大桥位于中国广东省珠江口伶仃洋海域内,是中国境内一项连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度和顶尖的建造技术而闻名世界.2018年10月24日上午9时开通运营后香港到澳门之间4个小时的陆路车程极大缩短.为了解实际通行所需时间,随机抽取了n台车辆进行统计,结果显示这些车辆的通行时间(单位:分钟)都在[35,50]内,按通行时间分为[35,38),[38,41),[41,44),[44,47),[47,50]五组,其中通行时间在[38,47)的车辆有182台,频率分布直方图如图所示,则n=( )
A.280 B.260 C.250 D.200
解:由题意可知,通行时间在[38,47)的频率为1﹣(0.01+0.02)×3=0.91,
所以,解得n=200.
故选:D.
8.已知函数f(x)=,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
A.﹣ B.﹣ C. D.
解:函数f(x)=,f′(x)=,
故f′(1)=,
所以曲线y=f(x)在点(1,f(1))处的切线的斜率为.
故选:C.
9.已知向量,满足||=3||,?=6,<,>=,则||=( )
A.2 B.3 C.4 D.6
解:因为?=cos<,>=||?||?cos=6,所以||=6.
故选:D.
10.如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,D为C1B1的中点,则异面直线A1C1与AD所成角的余弦值为( )
A. B. C. D.
解:如图,过点D作DF∥A1C1,交A1B1于点F,
则∠ADF为异面直线A1C1与AD所成角(或所成角的补角),
∵在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,
四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,D为C1B1的中点,
∴由题意知AD==,DF==,AF==,
∴异面直线A1C1与AD所成角的余弦值为:
cos∠ADF===.
故选:C.
11.函数y=(|x|﹣1)ln|x|的图象大致为( )
A. B.
C. D.
解:根据题意,f(x)=(|x|﹣1)ln|x|,有f(﹣x)=(|x|﹣1)ln|x|=f(x),
即函数y=(|x|﹣1)ln|x|为偶函数,排除A选项;
当0<x<1时,ln|x|<0,|x|﹣1<0,所以y=(|x|﹣1)ln|x|>0,排除B选项;
当x>1时,y=(x﹣1)lnx,,所以函数y=(|x|﹣1)ln|x|在(1,+∞)上单调递增,排除D选项.
故选:C.
12.已知离心率为的椭圆+y2=1(m>1)的左、右顶点分别为A,B,点P为该椭圆上一点,且P在第一象限,直线AP与直线x=4交于点C,直线BP与直线x=4交于点D,若|CD|=,则直线AP的斜率为( )
A.或 B. C.或 D.或
解:由,得m=9.
设p(x0,y0),则.
设kPA=k(0<k<),则,直线AP的方程为y=k(x+3),则C的坐标(4,7k).
直线BP的方程为y=,则D坐标(4,).
所以|CD|=7k+,解得k=(舍去)或.
故选:B.
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知函数f(x)=Asin(πx﹣3)+2的最小正周期为A,则f(x)的最大值为 4 .
解:∵函数f(x)=Asin(πx﹣3)+2的最小正周期为A,
∴A==2,
∴f(x)=2sin(πx﹣3)+2的最大值为4.
故答案为:4.
14.若双曲线C:x2﹣=1(b>0)的浙近线方程为y=±7x,则b= 7 .
解:双曲线C:x2﹣=1(b>0)的浙近线方程为y=±7x,
可得b=7.
故答案为:7.
15.已知定义域为R的函数f(x)满足f(﹣x)=﹣f(x),f(x+2)=﹣f(x),且当0<x≤1时,f(x)=2x2﹣log8x,则f(47)= ﹣2 .
解:∵函数f(x)满足f(﹣x)=﹣f(x),∴函数是奇函数,
f(x+2)=﹣f(x)=﹣f(x),
所以f(x+4)=﹣f(x+2)=f(x),
所以函数的周期为4,
当0<x≤1时,f(x)=2x2﹣log8x,
则f(47)=f(12×4﹣1)=f(﹣1)=﹣f(1)
=﹣(2×12﹣log81)=﹣2.
故答案为:﹣2.
16.如图,将一个圆柱2n(n∈N*)等分切割,再重新组合成一个与圆柱等底等高的几何体,当n越大,重新组合的几何体就越接近于一个“长方体”,若新几何体的表面积比圆柱的表面积增加了8,则圆柱的侧面积为 8π ,在满足前面条件且圆柱外接球表面积最小时,它的外接球体积为 .
解:设圆柱的底面半径为r,高h,外接球半径R,则2rh=8即hr=4,
所以圆柱的侧面积为2πrh=8π,
R2=≥rh=4即R≥2,当且仅当r==2时取等号,
此时外接球的表面积最小V==.
故答案为:8π;.
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤,考生根据要求作答,)
17.已知等差数列{an}的前n项和为Sn,且Sn=2n2+kn+k.
(1)求{an}的通项公式;
(2)若bn=,求数列{bn}的前n项和Tn.
解:(1)由题意,设等差数列{an}的公差为d,则
Sn=n2+(a1﹣)n=2n2+kn+k.
故,解得.
∴数列{an}的通项公式为an=2+4(n﹣1)=4n﹣2.
(2)由(1)知,
bn===?(﹣).
故Tn=b1+b2+…+bn
=?(1﹣)+?(﹣)+…+?(﹣)
=?(1﹣+﹣+…+﹣)
=?(1﹣)
=.
18.在△ABC中,角A,B,C的对边分别为a,b,c,且=.
(1)若△ABC的外接圆半径为,求b;
(2)若b=4,a+c=6,求△ABC的面积.
解:(1)△ABC中,角A,B,C的对边分别为a,b,c,且===,
由正弦定理可得=,
∴cos=sinB=2sincos,
∵cos≠0,
∴sin=,
∴=或=,(舍去),
∴B=,
∵△ABC的外接圆半径为,
∴=2R=2,
∴b=2×=3,
(2)由余弦定理可得b2=a2+c2﹣2accosB=(a+c)2﹣3ac,
即16=36﹣3ac,
∴ac=,
∴S△ABC=acsinB=××=.
19.在某公司举行的年会中,为了表彰年度优秀员工,该公司特意设置了二个抽奖环节,其规则如下,一个不透明的箱子中装有形状、大小相同的两个红色小球和四个绿色小球,从箱子中一次取出两个小球,同色奖励,不同色不奖励,一名优秀员工仅有一次抽奖机会若取出的两个均为红色,奖励2000元;若两个均为绿色,奖励1000元.
(1)求优秀员工小张获得2000元的概率;
(2)若一对夫妻均为年度优秀员工,求这对夫妻获得的奖励总金额X的分布列和数学期望.
解:(1)记“小张获得2000元”为事件A,
取出两个小球共有=15种情况,
其中两个小球均为红色共有=1种情况,
∴优秀员工小张获得2000元的概率为p(A)=.
(2)记“一名员工中奖1000元”为事件B,“一名员工不中奖”为事件C,
则P(B)==,
P(C)=1﹣P(A)﹣P(B)=,
由题知X所有的可能取值为0,1000,2000,3000,4000,
则P(X=0)=P(C)P(C)==,
P(X=1000)=2P(B)P(C)=2×=,
P(X=2000)=2P(A)P(C)+P(B)P(B)=+=,
P(X=3000)=2P(A)P(B)=2×=,
P(X=4000)=P(A)P(A)=,
∴X的分布列为:
X 0 1000 2000 3000 4000
P
E(X)=+=.
20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,BC∥AD,AB⊥AD,E为侧棱PA上一点,且AE=2PE,AP=3,AB=BC=2,AD=4.
(1)证明:PC∥平面BDE.
(2)求平面PCD与平面BDE所成锐二面角的余弦值.
解:(1)证明:连结AC,交BD于点F,连结EF,
∵BC∥AD,∴△BFC∽△DFA,∴,
∵=2.∴,∴EF∥PC,
∵EF?平面BDE,PC?平面BDE,
∴PC∥平面BDE.
(2)解:以A为坐标原点,建立空间直角坐标系A﹣xyz,如图所示,
则B(2,0,0),D(0,4,0),C(2,2,0),P(0,0,3),E(0,0,2),
则=(﹣2,2,0),=(0,4,﹣3),=(﹣2,4,0),=(0,4,﹣2),
设平面PCD的法向量=(x,y,z),
则,取x=3,得=(3,3,4),
设平面BDE的法向量=(a,b,c),
则,取b=1,得=(2,1,2),
cos<>===.
∴平面PCD与平面BDE所成锐二面角的余弦值为.
21.已知直线y=kx﹣3(k>1)与抛物线C;x2=﹣4y相交于A,B两点,且线段AB的中点为D(x0,y0).
(1)证明:y0<﹣5.
(2)过D作x轴的垂线,垂足为E,过E作直线AB的垂线,交C于M,N两点,求|MN|的取值范围.
解:(1)证明:由,可得x2+4kx﹣12=0,
设A(x1,y1),B(x2,y2),则x1+x2=﹣4k,
可得x0==﹣2k,y0=kx0﹣3=﹣2k2﹣3,
因为k>1,所以y0<﹣5;
(2)由题意,可得E的坐标为(﹣2k,0),
直线MN的方程为y=﹣(x+2k)即y=﹣x﹣2,
由可,得x2﹣x﹣8=0,
设M(x3,y3),N(x4,y4),可得x3+x4=,x3x4=﹣8,
△=+32>0恒成立,
|MN|=?==4,
由k>1,所以0<<1,则2<++2<6,
故|MN|的取值范围是(4,4).
22.已知函数f(x)=(x﹣m)ex﹣m.
(1)求f(x)的单调区间;
(2)若xlnx<e对x∈(1,+∞)恒成立,求a的取值范围.
解:(1)由f(x)=(x﹣m)ex﹣m,得f′(x)=(x﹣m+1)ex﹣m.
令f′(x)<0,得x<m﹣1,令f′(x)>0,得x>m﹣1.
∴f(x)的单调减区间为(﹣∞,m﹣1),单调递增区间为(m﹣1,+∞);
(2)当m=0时,f(x)=xex,由(1)知,f(x)在(0,+∞)上单调递增.
xlnx<e对x∈(1,+∞)恒成立,
即elnx?lnx<e对x∈(1,+∞)恒成立,
当x∈(1,+∞)时,lnx>0,x2>0,
当a<0时,不等式elnx?lnx<e显然不成立.
故a>0.
∴>0,则lnx<,即a<.
设函数g(x)=(x>1),则g′(x)=(x>1).
当1<x<时,g′(x)<0,当x>时,g′(x)>0,
∴.
故0<a<2e.
即a的取值范围是(0,2e).
同课章节目录
