11.1 全等三角形
图片预览





文档简介
(共20张PPT)
有作为才能创造地位, 常作为才能捍卫地位!
八年级数学
——吴祥贵
人教版新课程标准实验教材
(一)教材地位和作用
本小节是全章学习的开篇课,也是本章学习的主线和进一步学习其它图形的基础之一。
因此,本小节的教学对全章乃至以后的学习都是至关重要的。
在能力培养上,无论是逻辑思维能力、推理论证能力,还是分析问题解决问题的能力 ,都可在全等三角形教学中得以启迪和发展。
在知识结构上 ,以后学习的几何图形很多要通过全等三角形来加以解决;
教材分析
(二)学习任务分析
本节先通过形状、大小相同的图形引出 全等三角形 及其对应元素这些核心概念,然后直观演示图形的平移、翻折、旋转,从中体会图形变换的思想,逐步培养大家动态研究几何的意识,进而理解本节课的重点全等三角形的性质。
教材分析
(三)学生情况分析
本小节是在学过了线段、角、相交线、平行线、三角形的有关知识以及一些简单的说理内容之后来学习的,为学习全等三角形奠定了基础。
然而由于大家在图形识别能力上不足,而教材要求我们会确定全等三角形的对应元素也就成了大家有待突破的难点。
通过本小节的学习,可以丰富和加深我们对已学图形的认识,同时为学习其它图形知识打好基础。
教材分析
教学过程
(一)情境导入
活动1、情境问题:
配回打碎的
三角形玻璃
教学过程
(一)情境导入
活动2、观察:
教学过程
(一)情境导入
活动3、生活中的例子:
同一张底片洗出的同规格照片。
两张纸重合后的剪纸;
还有……?
教学过程
(一)情境导入
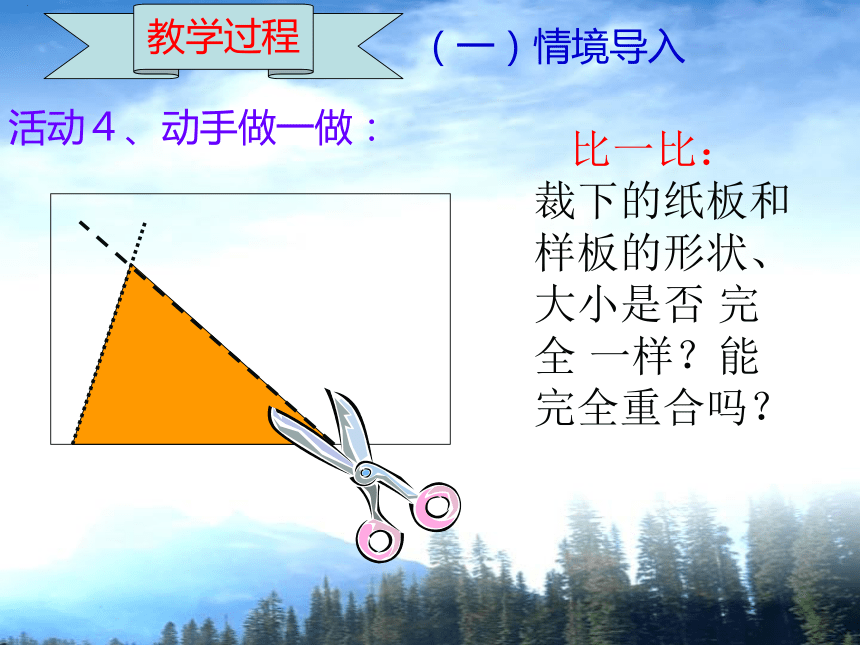
比一比: 裁下的纸板和样板的形状、大小是否 完 全 一样?能 完全重合吗?
活动4、动手做一做:
能够完全重合的两个图形;
全 等 形:
全等三角形:
定 义
能够完全重合的两个三角形。
A
B
C
D
F
E
(二)讲解新课
教学过程
1.全等三角形的定义
平移、翻折、旋转形状、大小都不变
结论:平移、翻折、旋转前后的图形全等。
⑴.平移
⑵.翻折
⑶.旋转
教学过程
2.三角形的变换
(二)讲解新课
A
C
B
F
E
D
想一想
能否记作 ABC≌ DEF
应该记作: ABC≌ DFE
原因:A与D、B与F、C与E对应。对应顶点要写在对应位置上。
A
B
C
D
F
E
教学过程
(二)讲解新课
3. 全等的对应元素及表示方法
记作: ABC≌ DEF
≌:读作“全等于”
(1)怎样的两条线段叫对应边?
(2)互相重合的两条线段的大小情况怎样?
可见,全等三角形的对应边相等
同理,全等三角形能够互相重合的两角是对应角,而能互相重合的两角大小是相等的。
所以,全等三角形的对应角相等
教学过程
(二)讲解新课
4. 全等三角形的性质
对应边相等,对应角相等
∴A B=D E,A C=D F,BC= E F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
如图,∵ ABC≌ DEF
(二)讲解新课
4. 全等三角形的性质
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
1、全等对应元素的找法
教学过程
(三)拓展与应用
小组活动
小组方案
方法提练
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边, 最小的边也是对应边;
(5)两个全等三角形最大的角是对应角, 最小的角也是对应角;
(2)将△ ABC 沿直线BC平移,得到△ DEF,说出图中线段、角的关系并说明理由。
A
B
C
D
E
O
A
F
E
D
C
B
(3)△ABD≌△ACE,若∠B=25°,BD=6㎝,AD=4㎝,你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么 ?
2、全等三角形性质的运用
教学过程
(三)拓展与应用
重点掌握:
明白道理:
“全等”和“对应相等”
因“完全重合”而“全等”
因“完全重合”而“对应”边(角)相等
口 诀: 形状相同大小等,完全重合是根本;
顶点一二三对应,边角相等方入门。
教学过程
交流:学会了什么? 收获了什么? 有什么感受?
课外作业:
1、P92-1、2、3
2、仿照图例,用全等形设计一幅美图,并附上一句诙谐的解说词.
天无绝人之路
我随奥运飞翔!
教学过程
谢谢合作
再见
有作为才能创造地位, 常作为才能捍卫地位!
八年级数学
——吴祥贵
人教版新课程标准实验教材
(一)教材地位和作用
本小节是全章学习的开篇课,也是本章学习的主线和进一步学习其它图形的基础之一。
因此,本小节的教学对全章乃至以后的学习都是至关重要的。
在能力培养上,无论是逻辑思维能力、推理论证能力,还是分析问题解决问题的能力 ,都可在全等三角形教学中得以启迪和发展。
在知识结构上 ,以后学习的几何图形很多要通过全等三角形来加以解决;
教材分析
(二)学习任务分析
本节先通过形状、大小相同的图形引出 全等三角形 及其对应元素这些核心概念,然后直观演示图形的平移、翻折、旋转,从中体会图形变换的思想,逐步培养大家动态研究几何的意识,进而理解本节课的重点全等三角形的性质。
教材分析
(三)学生情况分析
本小节是在学过了线段、角、相交线、平行线、三角形的有关知识以及一些简单的说理内容之后来学习的,为学习全等三角形奠定了基础。
然而由于大家在图形识别能力上不足,而教材要求我们会确定全等三角形的对应元素也就成了大家有待突破的难点。
通过本小节的学习,可以丰富和加深我们对已学图形的认识,同时为学习其它图形知识打好基础。
教材分析
教学过程
(一)情境导入
活动1、情境问题:
配回打碎的
三角形玻璃
教学过程
(一)情境导入
活动2、观察:
教学过程
(一)情境导入
活动3、生活中的例子:
同一张底片洗出的同规格照片。
两张纸重合后的剪纸;
还有……?
教学过程
(一)情境导入
比一比: 裁下的纸板和样板的形状、大小是否 完 全 一样?能 完全重合吗?
活动4、动手做一做:
能够完全重合的两个图形;
全 等 形:
全等三角形:
定 义
能够完全重合的两个三角形。
A
B
C
D
F
E
(二)讲解新课
教学过程
1.全等三角形的定义
平移、翻折、旋转形状、大小都不变
结论:平移、翻折、旋转前后的图形全等。
⑴.平移
⑵.翻折
⑶.旋转
教学过程
2.三角形的变换
(二)讲解新课
A
C
B
F
E
D
想一想
能否记作 ABC≌ DEF
应该记作: ABC≌ DFE
原因:A与D、B与F、C与E对应。对应顶点要写在对应位置上。
A
B
C
D
F
E
教学过程
(二)讲解新课
3. 全等的对应元素及表示方法
记作: ABC≌ DEF
≌:读作“全等于”
(1)怎样的两条线段叫对应边?
(2)互相重合的两条线段的大小情况怎样?
可见,全等三角形的对应边相等
同理,全等三角形能够互相重合的两角是对应角,而能互相重合的两角大小是相等的。
所以,全等三角形的对应角相等
教学过程
(二)讲解新课
4. 全等三角形的性质
对应边相等,对应角相等
∴A B=D E,A C=D F,BC= E F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
如图,∵ ABC≌ DEF
(二)讲解新课
4. 全等三角形的性质
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
1、全等对应元素的找法
教学过程
(三)拓展与应用
小组活动
小组方案
方法提练
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边, 最小的边也是对应边;
(5)两个全等三角形最大的角是对应角, 最小的角也是对应角;
(2)将△ ABC 沿直线BC平移,得到△ DEF,说出图中线段、角的关系并说明理由。
A
B
C
D
E
O
A
F
E
D
C
B
(3)△ABD≌△ACE,若∠B=25°,BD=6㎝,AD=4㎝,你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么 ?
2、全等三角形性质的运用
教学过程
(三)拓展与应用
重点掌握:
明白道理:
“全等”和“对应相等”
因“完全重合”而“全等”
因“完全重合”而“对应”边(角)相等
口 诀: 形状相同大小等,完全重合是根本;
顶点一二三对应,边角相等方入门。
教学过程
交流:学会了什么? 收获了什么? 有什么感受?
课外作业:
1、P92-1、2、3
2、仿照图例,用全等形设计一幅美图,并附上一句诙谐的解说词.
天无绝人之路
我随奥运飞翔!
教学过程
谢谢合作
再见
