11.4角平分线的性质(2)
文档属性
| 名称 | 11.4角平分线的性质(2) |  | |
| 格式 | rar | ||
| 文件大小 | 424.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-22 15:55:34 | ||
图片预览



文档简介
(共8张PPT)
1、回顾作一个已知角的角平分线;
2、探索角平分线上的点的性质并证明;
3、运用性质解决问题;
4、变式练习;
5、小结;
6、布置作业。
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵点P是∠AOB平分线上的一点
又PD⊥OA,PE⊥OB
∴ PD=PE
(角平分线上的点到角的两边的距离相等)
A
O
B
E
D
P
证明线段相等
有角的平分线,有垂直距离
应用定理的前提条件是:
定理的作用:
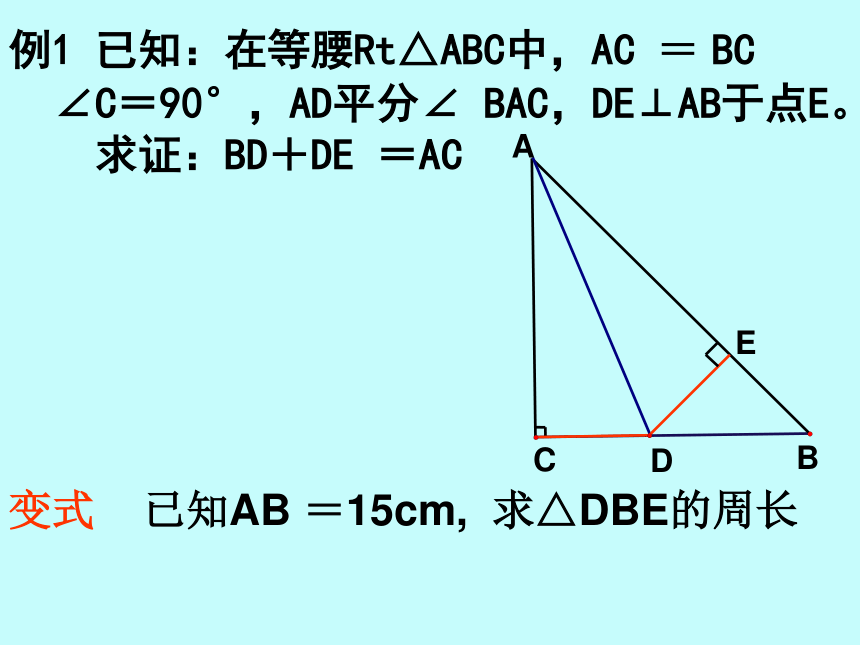
例1 已知:在等腰Rt△ABC中,AC = BC
∠C=90°,AD平分∠ BAC,DE⊥AB于点E。
求证:BD+DE =AC
变式 已知AB =15cm, 求△DBE的周长
E
D
C
B
A
D
E
F
A
B
C
P
1、应用角平分线的性质证题常用的
辅助线是什么?
2、三角形角平分线的交点有什么特征?
3、猜想如果点P是三角形的一个内角
平分线与一个外角平分线的交点,
结论是否仍成立?
4、如果点P是三角形的两个外角平分线
的交点,结论又会怎样?
5、完成讲义变式1、变式2。
1、角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3、定理的作用:证明线段相等
2、应用定理的前提条件是:
有角的平分线,有垂直距离
4、注意辅助线的作法
1、回顾作一个已知角的角平分线;
2、探索角平分线上的点的性质并证明;
3、运用性质解决问题;
4、变式练习;
5、小结;
6、布置作业。
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵点P是∠AOB平分线上的一点
又PD⊥OA,PE⊥OB
∴ PD=PE
(角平分线上的点到角的两边的距离相等)
A
O
B
E
D
P
证明线段相等
有角的平分线,有垂直距离
应用定理的前提条件是:
定理的作用:
例1 已知:在等腰Rt△ABC中,AC = BC
∠C=90°,AD平分∠ BAC,DE⊥AB于点E。
求证:BD+DE =AC
变式 已知AB =15cm, 求△DBE的周长
E
D
C
B
A
D
E
F
A
B
C
P
1、应用角平分线的性质证题常用的
辅助线是什么?
2、三角形角平分线的交点有什么特征?
3、猜想如果点P是三角形的一个内角
平分线与一个外角平分线的交点,
结论是否仍成立?
4、如果点P是三角形的两个外角平分线
的交点,结论又会怎样?
5、完成讲义变式1、变式2。
1、角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3、定理的作用:证明线段相等
2、应用定理的前提条件是:
有角的平分线,有垂直距离
4、注意辅助线的作法
