§2.1.1 指数与指数幂的运算(1)——根式
文档属性
| 名称 | §2.1.1 指数与指数幂的运算(1)——根式 |

|
|
| 格式 | rar | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-22 16:06:43 | ||
图片预览



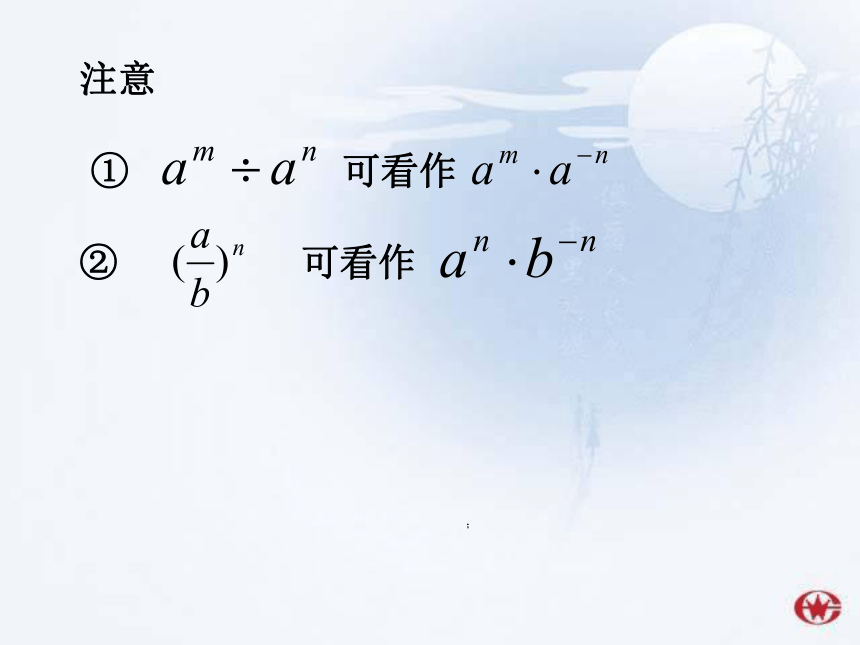



文档简介
(共19张PPT)
§2.1.1 指数与指数幂的运算(1)——根式
永昌四中 陈瑞天
*
an等于n个a的连乘积,即
an=a·a· ··· ·a
n个
正整数指数幂:
2)运算法则:
1)定义:
复习回顾
当m、n∈N+时
规定:
2.零指数幂、负整数指数幂:
an=a·a· ··· ·a
n个
正整数指数幂:
零指数幂、负整数指数幂:
整数指数幂:
定义
注意
① 可看作
② 可看作
;
运算法则:
当m、n∈Z时
3.整数指数幂的运算法则:
平方根(二次方根)
立方根(三次方根)
如果x2=a,则x叫做a的平方根.
如果x3=a,则x叫做a的立方根.
个数:
a>0
a=0
a<0
个数:
探索研究
如果存在实数x使得xn=a(a∈R,n﹥1,n ∈ N+),则x叫做a的n次方根.
1.n次方根的定义
例1.根据n次方根的概念,分别求出27的3次
方根,-32的5次方根,a6的3次方根。
(要求完整地叙述求解过程)
结论1:当n为奇数时(跟立方根一样),有下列
性质:正数的n次方根是正数,负数的n次方根是
负数,任何一个数的方根都是唯一的。此时,
a的n次方根可表示为
例2.根据n次方根的概念,分别求出
16的4次方根,-81的4次方根。
结论2:当n为偶数时(跟平方根一样)
有下列性质:正数的n次方根有两个且
互为相反数,负数没有n次方根。此时
正数a的n次方根可表示为:
其中
表示a的正的n次方根,
表示a的负的n次方根。
例3.根据n次方根的概念,分别求出0的3
次方根,0的4次方根。
结论3:0的n次方根是0,记作
当a=0时也有意义。
2. n次方根的个数:
a>0
a=0
a<0
n为偶数时
n为奇数时
(当n是奇数)
(当n是偶数,且a>0)
正数a的正n次方根叫做a的n次算术根.
3.根式的概念
根指数
被开方数
问题1:若对一个数先开方,再乘方(同次),
结果是什么?
,
例4:求
,
,
①
,即一个数先开方,再乘方
(同次),结果仍为被开方数。
②
问题2:若对一个数先乘方,再开方(同次),
结果又是什么?
探究:
4. 根式的运算性质
5. 乘方与开方
求a的n次方根,叫做把a开n次方,求一个数n次方根的运算称作开方运算.
开方运算与乘方运算互为逆运算.
6. 代数运算
加法、减法、乘法、除法、乘方、开方运算统称为代数运算.
求下列各式的值
达标检测
求下列各式的值:(1)
(2)
(3)
(4)
拓展练习
布置作业
教科书P59 习题2.1 A组 第1题
§2.1.1 指数与指数幂的运算(1)——根式
永昌四中 陈瑞天
*
an等于n个a的连乘积,即
an=a·a· ··· ·a
n个
正整数指数幂:
2)运算法则:
1)定义:
复习回顾
当m、n∈N+时
规定:
2.零指数幂、负整数指数幂:
an=a·a· ··· ·a
n个
正整数指数幂:
零指数幂、负整数指数幂:
整数指数幂:
定义
注意
① 可看作
② 可看作
;
运算法则:
当m、n∈Z时
3.整数指数幂的运算法则:
平方根(二次方根)
立方根(三次方根)
如果x2=a,则x叫做a的平方根.
如果x3=a,则x叫做a的立方根.
个数:
a>0
a=0
a<0
个数:
探索研究
如果存在实数x使得xn=a(a∈R,n﹥1,n ∈ N+),则x叫做a的n次方根.
1.n次方根的定义
例1.根据n次方根的概念,分别求出27的3次
方根,-32的5次方根,a6的3次方根。
(要求完整地叙述求解过程)
结论1:当n为奇数时(跟立方根一样),有下列
性质:正数的n次方根是正数,负数的n次方根是
负数,任何一个数的方根都是唯一的。此时,
a的n次方根可表示为
例2.根据n次方根的概念,分别求出
16的4次方根,-81的4次方根。
结论2:当n为偶数时(跟平方根一样)
有下列性质:正数的n次方根有两个且
互为相反数,负数没有n次方根。此时
正数a的n次方根可表示为:
其中
表示a的正的n次方根,
表示a的负的n次方根。
例3.根据n次方根的概念,分别求出0的3
次方根,0的4次方根。
结论3:0的n次方根是0,记作
当a=0时也有意义。
2. n次方根的个数:
a>0
a=0
a<0
n为偶数时
n为奇数时
(当n是奇数)
(当n是偶数,且a>0)
正数a的正n次方根叫做a的n次算术根.
3.根式的概念
根指数
被开方数
问题1:若对一个数先开方,再乘方(同次),
结果是什么?
,
例4:求
,
,
①
,即一个数先开方,再乘方
(同次),结果仍为被开方数。
②
问题2:若对一个数先乘方,再开方(同次),
结果又是什么?
探究:
4. 根式的运算性质
5. 乘方与开方
求a的n次方根,叫做把a开n次方,求一个数n次方根的运算称作开方运算.
开方运算与乘方运算互为逆运算.
6. 代数运算
加法、减法、乘法、除法、乘方、开方运算统称为代数运算.
求下列各式的值
达标检测
求下列各式的值:(1)
(2)
(3)
(4)
拓展练习
布置作业
教科书P59 习题2.1 A组 第1题
