§ 2.2.2 对数函数及其性质(4)——反函数的概念与求法
文档属性
| 名称 | § 2.2.2 对数函数及其性质(4)——反函数的概念与求法 |

|
|
| 格式 | rar | ||
| 文件大小 | 274.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-22 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
§ 2.2.2 对数函数及其性质(4)
——反函数的概念与求法
永昌四中 陈瑞天
*
一个学生到超市买笔记本,每个2元
(1)所用钱数y与购买个数X之间的关系式
是 _______________
(2)购买个数X与所用钱数y之间的关系式
是 _______________
y=2x (x∈N)
x=y/2
x=y/2(y∈ B)是函数吗
是
我们把 x=y/2 (y∈ B)叫做y=2x (x∈N)
的反函数.
(y∈ B) B={y | y=2n,n∈N}
问题情境
函数 y=2x x=y/2
x,y的关系
对应法则
定义域
值域
x是自变量,y是函数
自变量的2倍
N
B
B
B={y | y=2n,n∈N}
y是自变量,x是函数
自变量的1/2倍
N
探索研究
记作:x=f-1(y)
字母x、y互换,得 y=f-1(x)
一般地,函数y=f(x)(x A)中,设它的值域为C,我们根据这个函数中x,y的关系,用y把x表示出,得到x=φ(y),如果对于 y在 C中的任何一个值,通过x= φ (y),x在A中都有唯一的值和它对应,那么,x= φ(y)就表示y是自变量,x是自变量y的函数,这样的函数x = φ (y)(y C)叫做函数y=f(x)(x A)的反函数。
1.反函数定义:
即:y=f (x)与y=f-1(x)互为反函数
对反函数定义的理解
(1)反函数也是函数,因为它是符合函数定义的;
(2)原来函数与反函数的法则互逆;它们互为反函数;
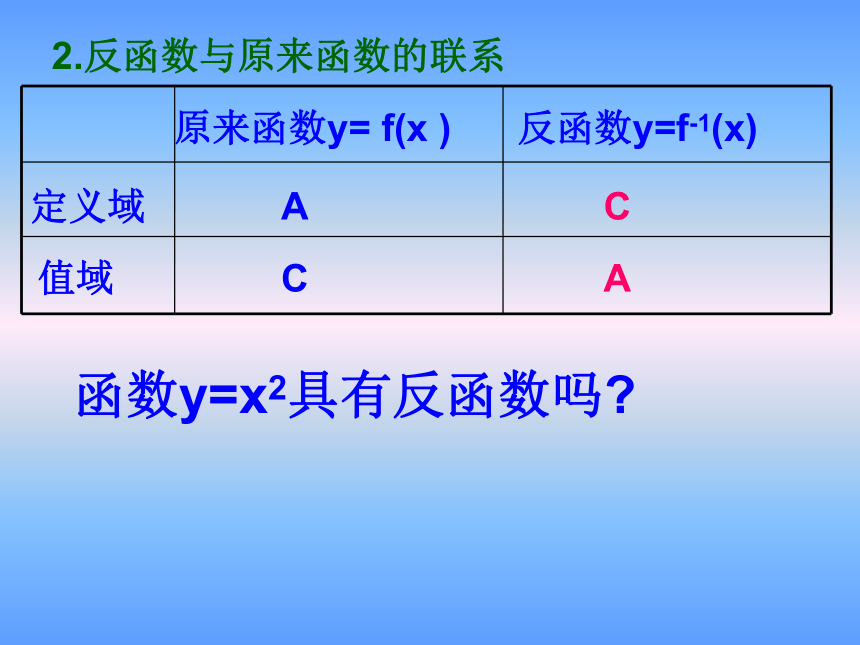
定义域
值域
原来函数y= f(x )
反函数y=f-1(x)
C
C
A
A
2.反函数与原来函数的联系
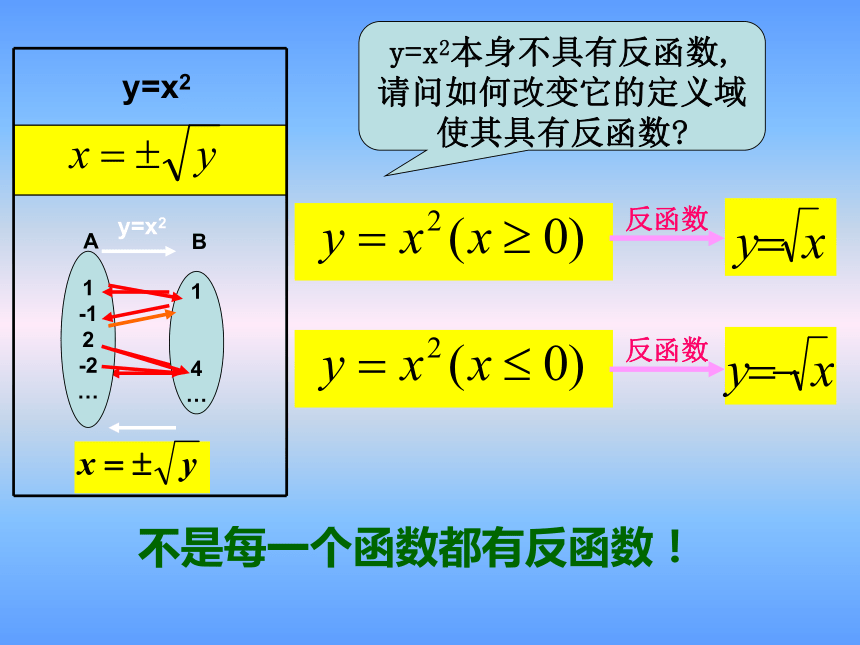
函数y=x2具有反函数吗
y=x2
y=x2本身不具有反函数,请问如何改变它的定义域使其具有反函数
反函数
反函数
A
B
1
-1
2
-2
…
1
4
…
y=x2
不是每一个函数都有反函数!
一个函数有反函数的充要条件是它相应的映射是一一映射
3.反函数存在的条件
问题:单调函数一定有反函数吗?反函数一定单调吗?
结论:单调函数必有反函数,反函数未必单调.
解:
(1)由 函数 ,解得
所以,函数 的反函数是
例1.求下列函数的反函数:
(1)
(2)
(3)
(4)
(2)由 函数 ,解得
所以,函数 的反函数是
(3)由 函数 ,解得
所以,函数 的反函数是
(4)由 函数 ,解得
所以,函数 的反函数是
(1)写出原来函数的定义域和值域
(2)由y=f(x)反解得x=f-1(y)
(3)把x、y互换
(4)写出反函数的定义域
4、求反函数的步骤:
例2.求函数y= 0 (x=0) 的反函数.
(x>0)
(x<0)
y = 0 x = 0
x – 1 x > 1
– – x – 1 x < – 1
1、求函数
的反函数
2、已知函数 的反函数是其本身,则
a= ———
-1
达标检测
1 反函数的定义
2 求反函数的步骤
3 并不是所有的函数都具有反函数
只有满足一一映射的函数才具有反函数
(1)反解出x
(2)交换x,y的位置
(3)求出原来函数的值域
作为反函数的定义域
(4)下结论
总结提炼
布置作业
1.求函数
的反函数.
§ 2.2.2 对数函数及其性质(4)
——反函数的概念与求法
永昌四中 陈瑞天
*
一个学生到超市买笔记本,每个2元
(1)所用钱数y与购买个数X之间的关系式
是 _______________
(2)购买个数X与所用钱数y之间的关系式
是 _______________
y=2x (x∈N)
x=y/2
x=y/2(y∈ B)是函数吗
是
我们把 x=y/2 (y∈ B)叫做y=2x (x∈N)
的反函数.
(y∈ B) B={y | y=2n,n∈N}
问题情境
函数 y=2x x=y/2
x,y的关系
对应法则
定义域
值域
x是自变量,y是函数
自变量的2倍
N
B
B
B={y | y=2n,n∈N}
y是自变量,x是函数
自变量的1/2倍
N
探索研究
记作:x=f-1(y)
字母x、y互换,得 y=f-1(x)
一般地,函数y=f(x)(x A)中,设它的值域为C,我们根据这个函数中x,y的关系,用y把x表示出,得到x=φ(y),如果对于 y在 C中的任何一个值,通过x= φ (y),x在A中都有唯一的值和它对应,那么,x= φ(y)就表示y是自变量,x是自变量y的函数,这样的函数x = φ (y)(y C)叫做函数y=f(x)(x A)的反函数。
1.反函数定义:
即:y=f (x)与y=f-1(x)互为反函数
对反函数定义的理解
(1)反函数也是函数,因为它是符合函数定义的;
(2)原来函数与反函数的法则互逆;它们互为反函数;
定义域
值域
原来函数y= f(x )
反函数y=f-1(x)
C
C
A
A
2.反函数与原来函数的联系
函数y=x2具有反函数吗
y=x2
y=x2本身不具有反函数,请问如何改变它的定义域使其具有反函数
反函数
反函数
A
B
1
-1
2
-2
…
1
4
…
y=x2
不是每一个函数都有反函数!
一个函数有反函数的充要条件是它相应的映射是一一映射
3.反函数存在的条件
问题:单调函数一定有反函数吗?反函数一定单调吗?
结论:单调函数必有反函数,反函数未必单调.
解:
(1)由 函数 ,解得
所以,函数 的反函数是
例1.求下列函数的反函数:
(1)
(2)
(3)
(4)
(2)由 函数 ,解得
所以,函数 的反函数是
(3)由 函数 ,解得
所以,函数 的反函数是
(4)由 函数 ,解得
所以,函数 的反函数是
(1)写出原来函数的定义域和值域
(2)由y=f(x)反解得x=f-1(y)
(3)把x、y互换
(4)写出反函数的定义域
4、求反函数的步骤:
例2.求函数y= 0 (x=0) 的反函数.
(x>0)
(x<0)
y = 0 x = 0
x – 1 x > 1
– – x – 1 x < – 1
1、求函数
的反函数
2、已知函数 的反函数是其本身,则
a= ———
-1
达标检测
1 反函数的定义
2 求反函数的步骤
3 并不是所有的函数都具有反函数
只有满足一一映射的函数才具有反函数
(1)反解出x
(2)交换x,y的位置
(3)求出原来函数的值域
作为反函数的定义域
(4)下结论
总结提炼
布置作业
1.求函数
的反函数.
