2.3.2 幂函数性质的应用
图片预览




文档简介
(共13张PPT)
2.3.2 幂函数性质的应用
永昌四中
任兰兰
定义域
值 域
奇偶性
单调性
定 点
复习回顾
幂函数的图象特征和性质:
1. >0时,
(1)图象都经过点(0,0)和(1,1);
(2)图象在第一象限是上升的,即在 上是增 函数.
(3)图象呈“抛物线”型的弧.
2. <0时
(1)图象都经过点(1,1);
(2)图象在第一象限是下降的,且向右无限接近X
轴,向上无限接近Y轴,即在 上是
减函数.
(3)图象呈“双曲线”型的弧.
在直线x=1右侧,幂指数越大,图象越高,即越远
离x轴;即x>1时,当函数的自变量相等时,幂指
数越大,函数值越大
4,在直线x=1左侧,幂指数越大,图象越低,即越
靠近x轴;即0指数越大,函数值越小
第一象限内幂函数图像的特点
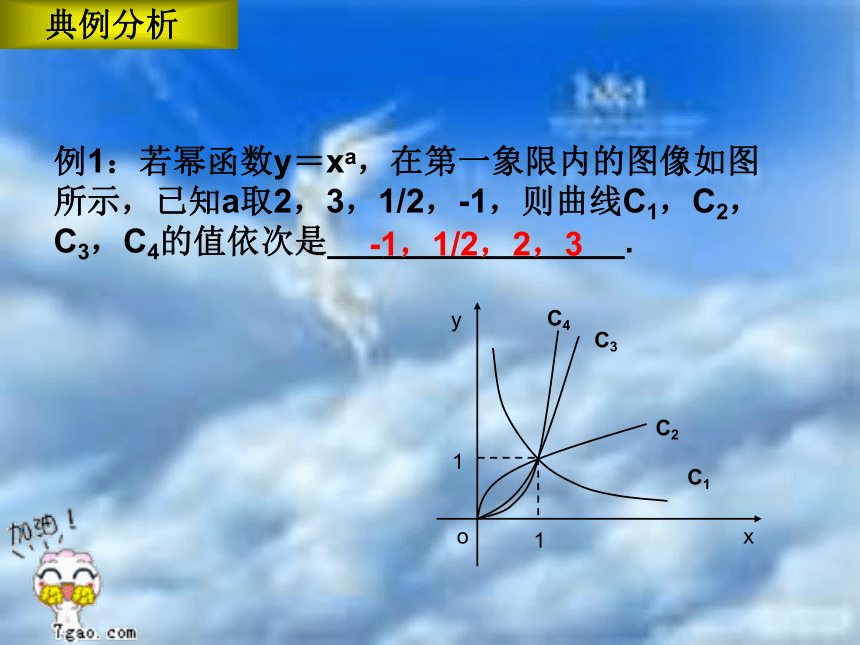
例1:若幂函数y=xa,在第一象限内的图像如图
所示,已知a取2,3,1/2,-1,则曲线C1,C2,
C3,C4的值依次是________________.
o
x
y
1
1
C1
C2
C3
C4
-1,1/2,2,3
典例分析
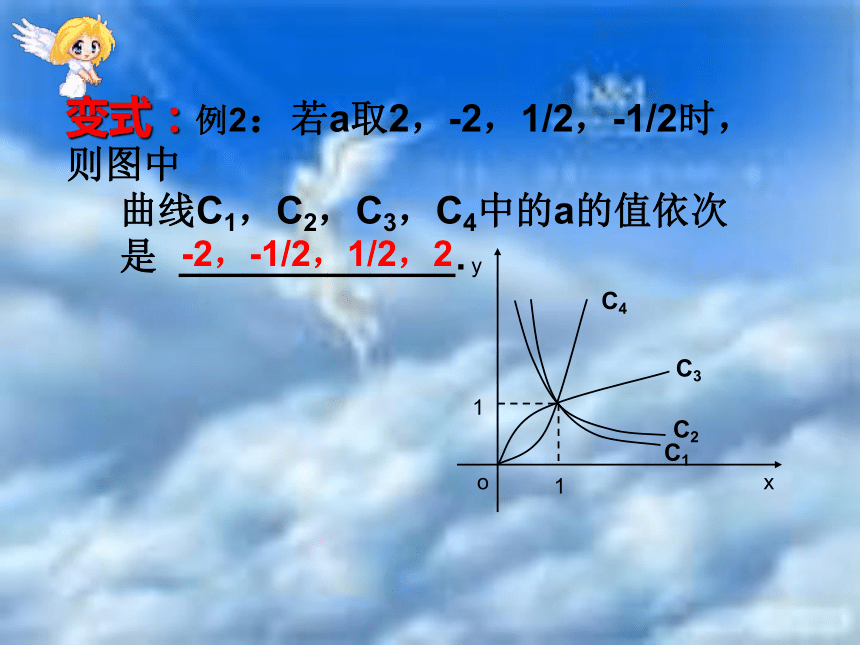
变式:例2:若a取2,-2,1/2,-1/2时,则图中
曲线C1,C2,C3,C4中的a的值依次
是 _____________.
o
x
y
1
1
C1
C2
C3
C4
-2,-1/2,1/2,2
例2:幂函数f(x)的图象过点(2, ),求
分析:本题可利用待定系数法
解:设y=xa
∵当x=2时,y=1/4
∴1/4=2a,即2a=2-2
∴a=-2
∴f(x)=x-2
∴ f(1/2)=(1/2)-2 = 4
例4
已知函数
(1) m为何值时,f(x)是正比例函数;
(2) m为何值时,f(x)是反比例函数;
(3) m为何值时,f(x)是二次函数;
(4) m为何值时,f(x)是幂函数;
分析:函数
当 且 ,f(x)时正比例函数;
当 且 , f(x)时反比例函数;
当 且 , f(x)时二次函数;
当 且 , f(x)时幂函数;
1.函数
是幂函数,且在
上是减函数,求实数m
m=2
课堂练习
2 幂函数f(x)=xa ,f(x)=xb ,f(x)=xc, f(x)=xd,在第一象限的图象如图所示,则a,b,c,d的大小关系
是( )
(A)a>b>c>d
(B)d>b>c>a
(C)d>c>b>a
(D)b>c>d>a
答案:D
1,若 ,求a的取值范围
2,已知幂函数f(x)存在反函数 ,
且 求f(x)的解析式
3,已知函数 (a为常数)
(1)a为何值时,此函数为幂函数?
(2) a为何值时,此函数为正比例函数?
(3) a为何值时,此函数为反比例函数?
布置作业
下 课 了 !
2.3.2 幂函数性质的应用
永昌四中
任兰兰
定义域
值 域
奇偶性
单调性
定 点
复习回顾
幂函数的图象特征和性质:
1. >0时,
(1)图象都经过点(0,0)和(1,1);
(2)图象在第一象限是上升的,即在 上是增 函数.
(3)图象呈“抛物线”型的弧.
2. <0时
(1)图象都经过点(1,1);
(2)图象在第一象限是下降的,且向右无限接近X
轴,向上无限接近Y轴,即在 上是
减函数.
(3)图象呈“双曲线”型的弧.
在直线x=1右侧,幂指数越大,图象越高,即越远
离x轴;即x>1时,当函数的自变量相等时,幂指
数越大,函数值越大
4,在直线x=1左侧,幂指数越大,图象越低,即越
靠近x轴;即0
第一象限内幂函数图像的特点
例1:若幂函数y=xa,在第一象限内的图像如图
所示,已知a取2,3,1/2,-1,则曲线C1,C2,
C3,C4的值依次是________________.
o
x
y
1
1
C1
C2
C3
C4
-1,1/2,2,3
典例分析
变式:例2:若a取2,-2,1/2,-1/2时,则图中
曲线C1,C2,C3,C4中的a的值依次
是 _____________.
o
x
y
1
1
C1
C2
C3
C4
-2,-1/2,1/2,2
例2:幂函数f(x)的图象过点(2, ),求
分析:本题可利用待定系数法
解:设y=xa
∵当x=2时,y=1/4
∴1/4=2a,即2a=2-2
∴a=-2
∴f(x)=x-2
∴ f(1/2)=(1/2)-2 = 4
例4
已知函数
(1) m为何值时,f(x)是正比例函数;
(2) m为何值时,f(x)是反比例函数;
(3) m为何值时,f(x)是二次函数;
(4) m为何值时,f(x)是幂函数;
分析:函数
当 且 ,f(x)时正比例函数;
当 且 , f(x)时反比例函数;
当 且 , f(x)时二次函数;
当 且 , f(x)时幂函数;
1.函数
是幂函数,且在
上是减函数,求实数m
m=2
课堂练习
2 幂函数f(x)=xa ,f(x)=xb ,f(x)=xc, f(x)=xd,在第一象限的图象如图所示,则a,b,c,d的大小关系
是( )
(A)a>b>c>d
(B)d>b>c>a
(C)d>c>b>a
(D)b>c>d>a
答案:D
1,若 ,求a的取值范围
2,已知幂函数f(x)存在反函数 ,
且 求f(x)的解析式
3,已知函数 (a为常数)
(1)a为何值时,此函数为幂函数?
(2) a为何值时,此函数为正比例函数?
(3) a为何值时,此函数为反比例函数?
布置作业
下 课 了 !
