§ 1.1.2 集合间的基本关系
文档属性
| 名称 | § 1.1.2 集合间的基本关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-22 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
§ 1.1.2 集合间的基本关系
永昌四中 陈瑞天
*
实数有相等关系、大小关系,如5=5,5<7,5>3,等等,类比实数之间的关系,你会想到集合之间的什么关系?
思考
问题情境
观察下面几个例子,你能发现两个集合之间的关系吗?
⑴ A={1,2,3} , B={1,2,3,4,5};
⑵设A为永昌四中高一(4)班女生的全体组成的集合,
B为这个班学生的全体组成的集合;
⑶ 设C={x|x是两条边相等的三角形},D={x|x是等腰三角形}.
探索研究
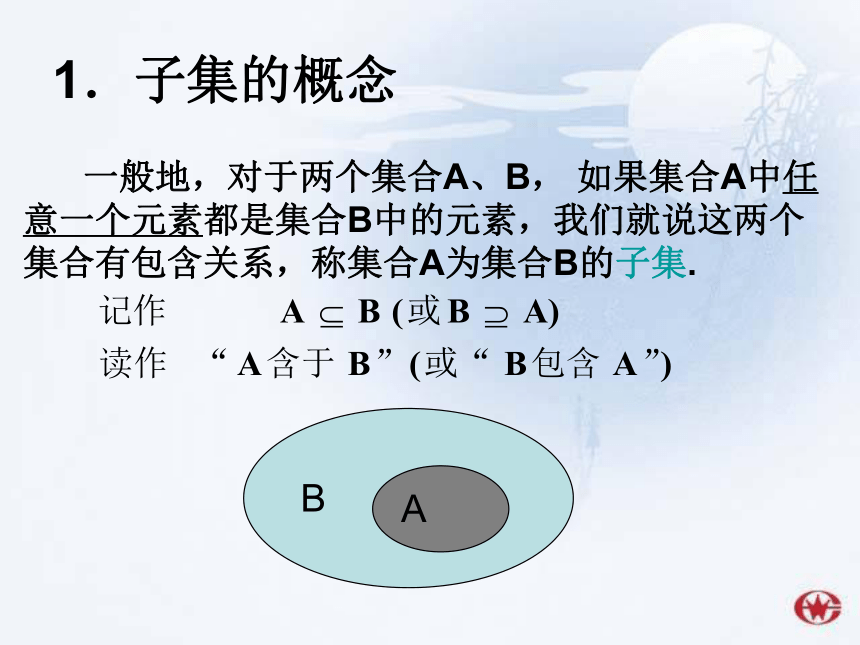
1.子集的概念
一般地,对于两个集合A、B, 如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集.
B
A
B
A B
A
注:有两种可能
(1)A是B的一部分;
(2)A与B是同一集合
B
A
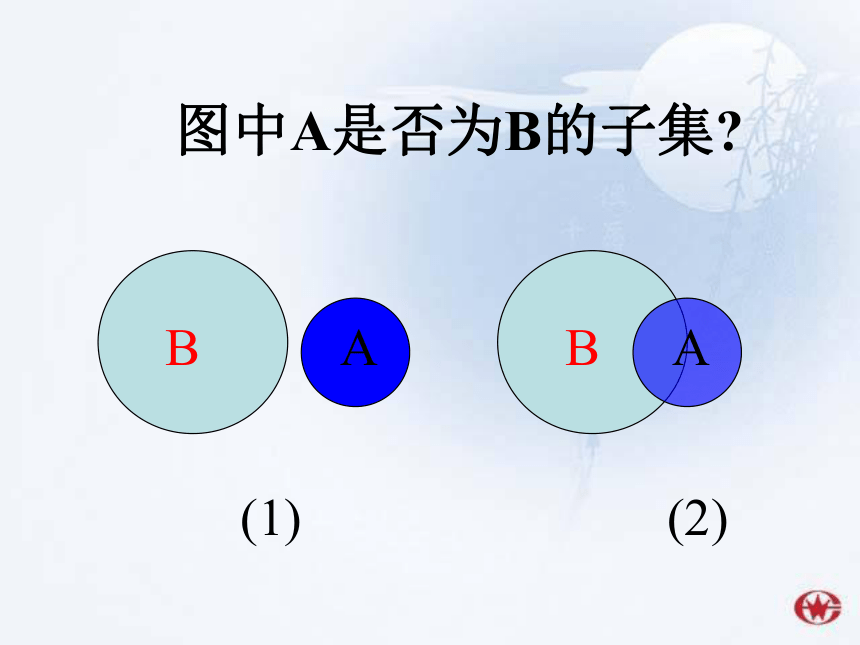
图中A是否为B的子集
(1)
B
A
(2)
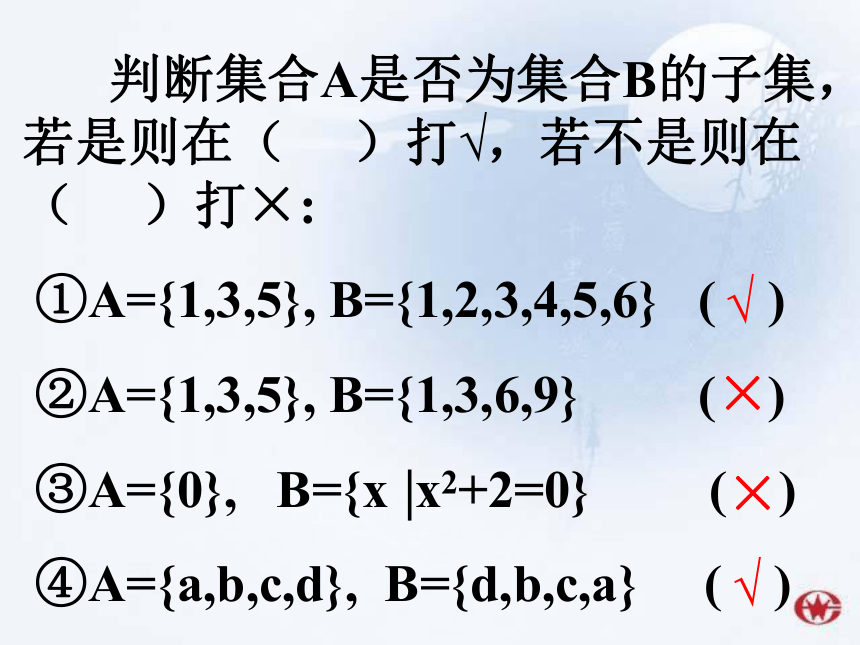
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
×
×
√
√
2.集合相等与真子集的概念
A
B
3.空集
空集是任何非空集合的真子集.
4.几个结论
①空集是任何集合的子集Φ A
②空集是任何非空集合的真子集
Φ A (A ≠ Φ)
③任何一个集合是它本身的子集,
即 A A
④对于集合A,B,C,如果 A B,
且B C,则A C
注意易混符号
①“∈ ”与“ ”:元素与集合之间是属于关系;集合与集合之间是包含关系如
Φ R,{1} {1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合如
Φ {0}不能写成Φ={0},Φ∈{0}
例1(1) 写出N,Z,Q,R的包含关系,并用Venn图表示
(2) 判断下列写法是否正确
①Φ A ②Φ A
③ A A ④A A
典例分析
答案:1
重要结论
结论:含n个元素的集合的所有子集的个数是2n,
所有真子集的个数是2n-1,非空真子集数为2n-2.
设集合A={x|1≤x≤3},B={x|x-a≥0}若A是B的真子集,求实数a的取值范围。
拓展练习
子集、真子集的定义
集合之间的关系
空集是任何集合的子集,是任何非空集合的真子集
总结提炼
教材P11~12 A组 第5题
布置作业
§ 1.1.2 集合间的基本关系
永昌四中 陈瑞天
*
实数有相等关系、大小关系,如5=5,5<7,5>3,等等,类比实数之间的关系,你会想到集合之间的什么关系?
思考
问题情境
观察下面几个例子,你能发现两个集合之间的关系吗?
⑴ A={1,2,3} , B={1,2,3,4,5};
⑵设A为永昌四中高一(4)班女生的全体组成的集合,
B为这个班学生的全体组成的集合;
⑶ 设C={x|x是两条边相等的三角形},D={x|x是等腰三角形}.
探索研究
1.子集的概念
一般地,对于两个集合A、B, 如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集.
B
A
B
A B
A
注:有两种可能
(1)A是B的一部分;
(2)A与B是同一集合
B
A
图中A是否为B的子集
(1)
B
A
(2)
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
×
×
√
√
2.集合相等与真子集的概念
A
B
3.空集
空集是任何非空集合的真子集.
4.几个结论
①空集是任何集合的子集Φ A
②空集是任何非空集合的真子集
Φ A (A ≠ Φ)
③任何一个集合是它本身的子集,
即 A A
④对于集合A,B,C,如果 A B,
且B C,则A C
注意易混符号
①“∈ ”与“ ”:元素与集合之间是属于关系;集合与集合之间是包含关系如
Φ R,{1} {1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合如
Φ {0}不能写成Φ={0},Φ∈{0}
例1(1) 写出N,Z,Q,R的包含关系,并用Venn图表示
(2) 判断下列写法是否正确
①Φ A ②Φ A
③ A A ④A A
典例分析
答案:1
重要结论
结论:含n个元素的集合的所有子集的个数是2n,
所有真子集的个数是2n-1,非空真子集数为2n-2.
设集合A={x|1≤x≤3},B={x|x-a≥0}若A是B的真子集,求实数a的取值范围。
拓展练习
子集、真子集的定义
集合之间的关系
空集是任何集合的子集,是任何非空集合的真子集
总结提炼
教材P11~12 A组 第5题
布置作业
