§ 1.1.3 集合的基本运算(2)
文档属性
| 名称 | § 1.1.3 集合的基本运算(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 691.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-22 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
§ 1.1.3 集合的基本运算(2)
永昌四中 陈瑞天
*
①用列举法表示下列集合:
探索研究
④问题①,集合Z,Q,R分别含有所解方程时所涉及的全部元素,这样的集合称为全集,请给出全集的定义.
②问题①中三个集合相等吗?为什么?
③由此看,解方程时要注意什么?
1.全集的定义
全集常用U表示.
如果一个集合含有我们所要研究的各个集合的全部元素,这个就称这个集合为全集(universe set)
⑤已知全集U={1,2,3},A={1},写出全集中不属于集合A的所有元素组成的集合B.
⑥问题⑤中集合B称为集合A相对于全集U的补集,请给出补集的定义.
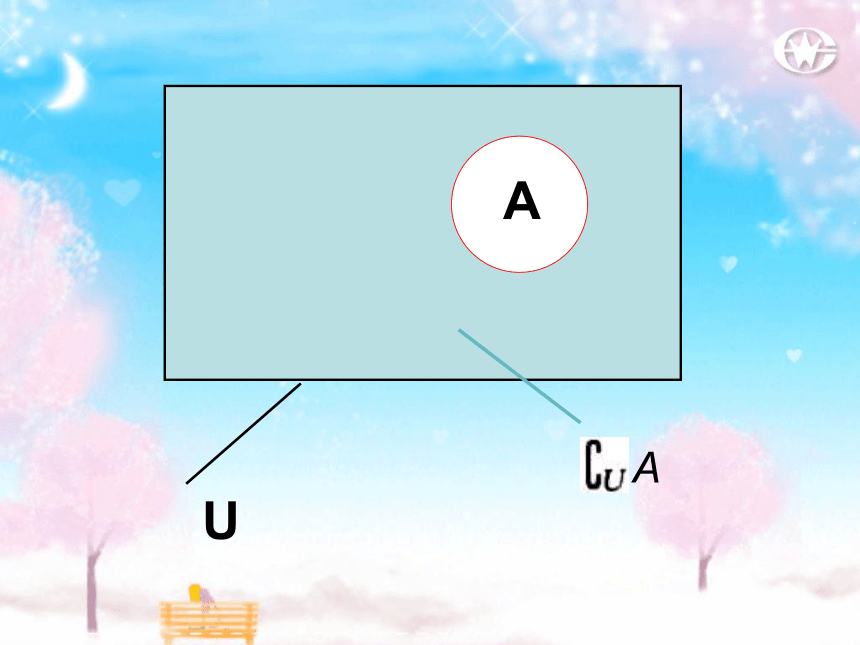
对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集,记作
2.补集的定义
A
即:
U
A
A
例1 设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CUA, CUB
例2.设U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.求A∩B, CU (A∪B)
例3.已知全集U=R,集合A={x|1≤2x+1<9},求CUA
用card来表示有限集A中的元素个数.
如:A={a,b,c} 则card(A)=3
3.集合中元素的个数
学校小卖部进了两次货,第一次进的货是圆珠笔,钢笔,橡皮,笔记本,方便面,汽水共6种,第二次进的货是圆珠笔,铅笔,火腿肠,方便面共4种,两次一共进了几种货物
问题:
card(A∪B)=card(A)+card(B)-card(A∩B)
公式:
例4.学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,这个班有12名学生参赛,两次运动会都参赛的有3人,两次运动会中,这个班共有多少名同学参赛
探索:
对有限集A,B,C你能发现card(A∪B∪C), card(A), card(B), card(C), card(A∩B), card(A∩C), card(C∩B), card(A∩B∩C)之间的关系吗
A
B
C
A∩B
B∩C
A∩C
A∩B∩C
利用Venn图:
card(A∪B∪C)=card(A)+ card(B)+ card(C)
- card(A∩B)- card(A∩C)- card(C∩B)+ card(A∩B∩C)
教材P12 9,10 B组 4
布置作业
教材P11练习 1~3.
达标检测
1. 理解两个集合交集与并集的概念和性质.
2. 求两个集合的交集与并集,常用图示法(数轴、坐标平面、韦恩图).
4. 注意对字母要进行讨论 .
3.注意灵活、准确地运用性质解题;
总结提炼
1.教材P12 A组6,7,8 B组3
2 补.P={a2,a+2,-3},
Q={a-2,2a+1,a2+1},P ∩Q={-3},
求a.
布置作业
§ 1.1.3 集合的基本运算(2)
永昌四中 陈瑞天
*
①用列举法表示下列集合:
探索研究
④问题①,集合Z,Q,R分别含有所解方程时所涉及的全部元素,这样的集合称为全集,请给出全集的定义.
②问题①中三个集合相等吗?为什么?
③由此看,解方程时要注意什么?
1.全集的定义
全集常用U表示.
如果一个集合含有我们所要研究的各个集合的全部元素,这个就称这个集合为全集(universe set)
⑤已知全集U={1,2,3},A={1},写出全集中不属于集合A的所有元素组成的集合B.
⑥问题⑤中集合B称为集合A相对于全集U的补集,请给出补集的定义.
对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集,记作
2.补集的定义
A
即:
U
A
A
例1 设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CUA, CUB
例2.设U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.求A∩B, CU (A∪B)
例3.已知全集U=R,集合A={x|1≤2x+1<9},求CUA
用card来表示有限集A中的元素个数.
如:A={a,b,c} 则card(A)=3
3.集合中元素的个数
学校小卖部进了两次货,第一次进的货是圆珠笔,钢笔,橡皮,笔记本,方便面,汽水共6种,第二次进的货是圆珠笔,铅笔,火腿肠,方便面共4种,两次一共进了几种货物
问题:
card(A∪B)=card(A)+card(B)-card(A∩B)
公式:
例4.学校先举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,这个班有12名学生参赛,两次运动会都参赛的有3人,两次运动会中,这个班共有多少名同学参赛
探索:
对有限集A,B,C你能发现card(A∪B∪C), card(A), card(B), card(C), card(A∩B), card(A∩C), card(C∩B), card(A∩B∩C)之间的关系吗
A
B
C
A∩B
B∩C
A∩C
A∩B∩C
利用Venn图:
card(A∪B∪C)=card(A)+ card(B)+ card(C)
- card(A∩B)- card(A∩C)- card(C∩B)+ card(A∩B∩C)
教材P12 9,10 B组 4
布置作业
教材P11练习 1~3.
达标检测
1. 理解两个集合交集与并集的概念和性质.
2. 求两个集合的交集与并集,常用图示法(数轴、坐标平面、韦恩图).
4. 注意对字母要进行讨论 .
3.注意灵活、准确地运用性质解题;
总结提炼
1.教材P12 A组6,7,8 B组3
2 补.P={a2,a+2,-3},
Q={a-2,2a+1,a2+1},P ∩Q={-3},
求a.
布置作业
