§ 1.3.1 单调性与最大(小)值(一)——函数的单调性
文档属性
| 名称 | § 1.3.1 单调性与最大(小)值(一)——函数的单调性 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-22 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
§ 1.3.1 单调性与最大(小)值(一)
——函数的单调性
永昌四中 陈瑞天
*
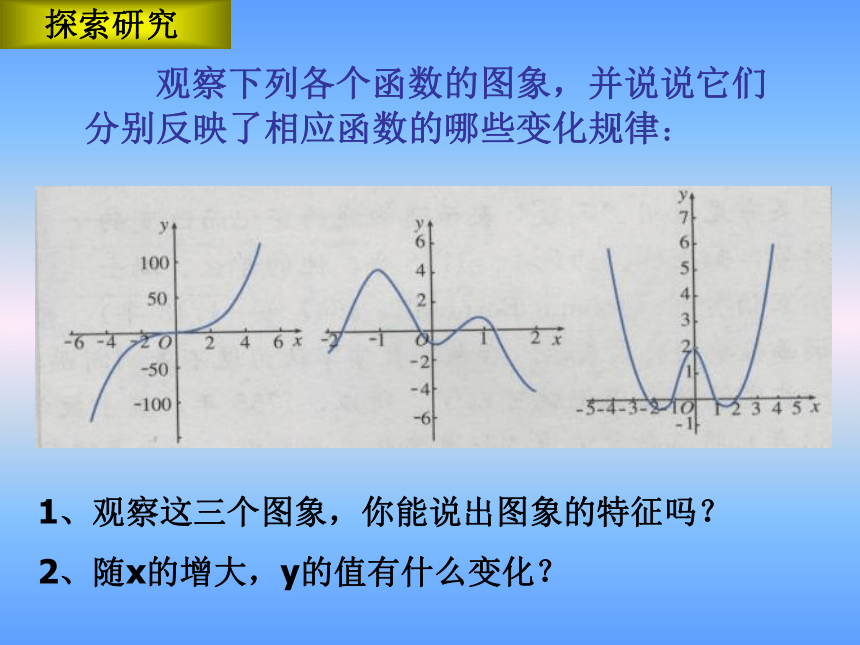
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
1、观察这三个图象,你能说出图象的特征吗?
2、随x的增大,y的值有什么变化?
探索研究
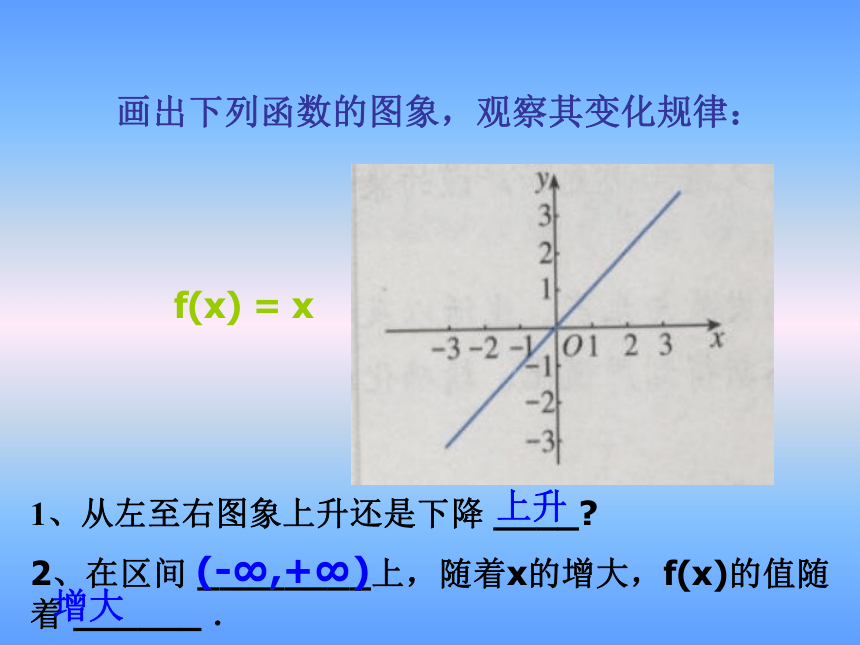
画出下列函数的图象,观察其变化规律:
1、从左至右图象上升还是下降 ____
2、在区间 ________上,随着x的增大,f(x)的值随着 ______ .
f(x) = x
(-∞,+∞)
增大
上升
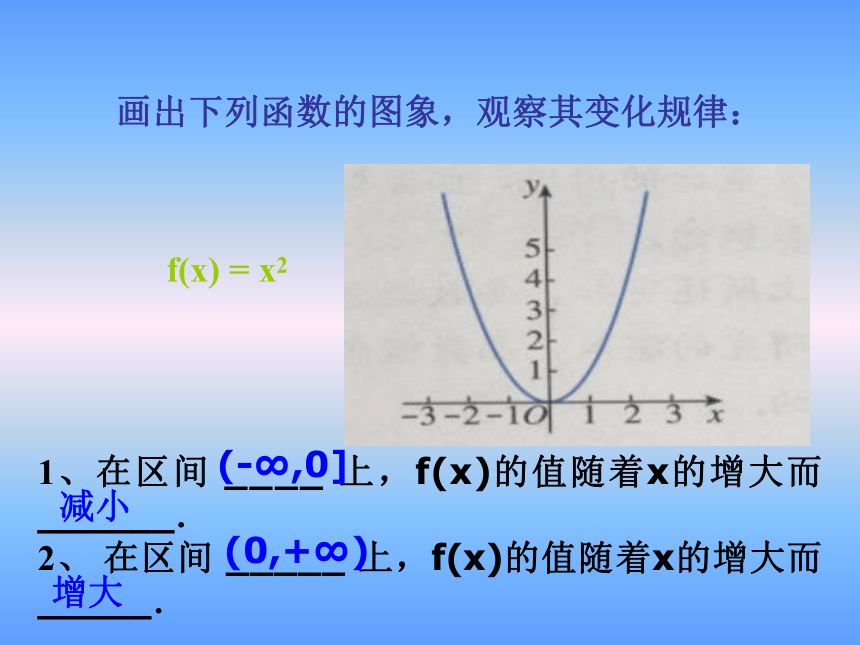
1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____.
f(x) = x2
(-∞,0]
(0,+∞)
增大
减小
画出下列函数的图象,观察其变化规律:
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x)=x2 … 16 9 4 1 0 1 4 9 16 …
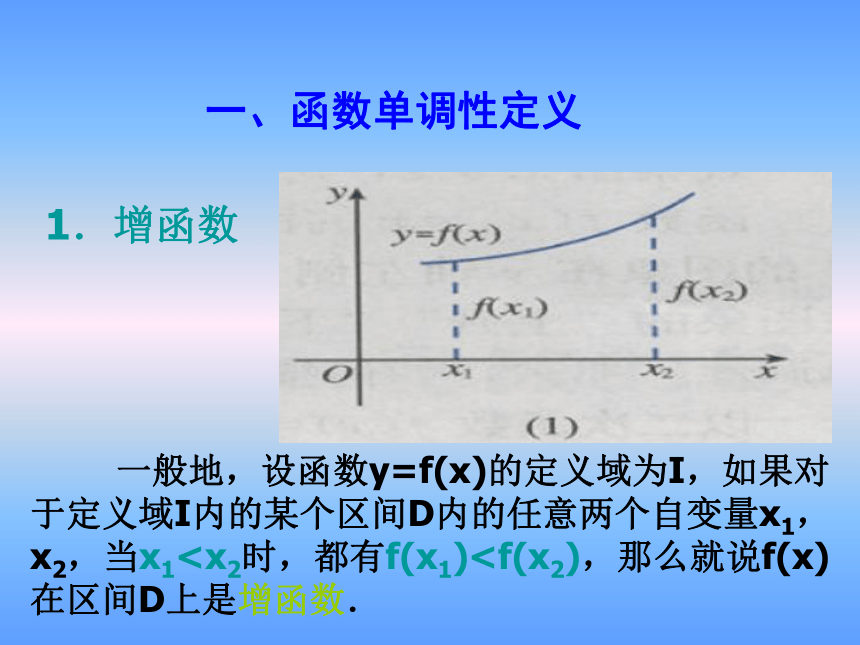
一、函数单调性定义
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x11.增函数
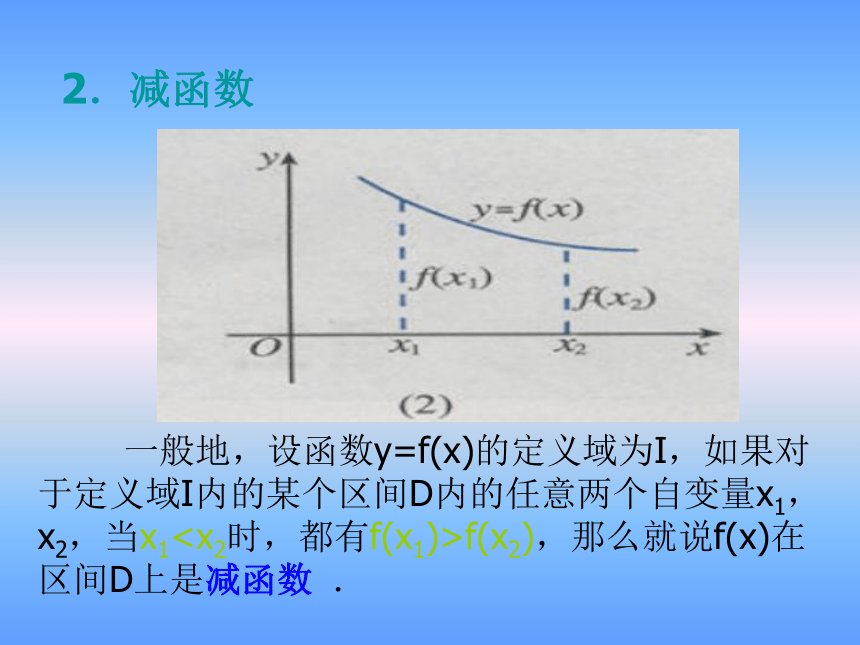
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在区间D上是减函数 .
2.减函数
1、函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
注意:
2 、必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2) 分别是增函数和减函数.
如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
二.函数的单调性定义
y
o
x
o
y
x
y
o
x
y
o
x
y
o
x
在
增函数
在
减函数
在
增函数
在
减函数
在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数
在(-∞,+∞)是增函数
在(-∞,0)和(0,+∞)是增函数
y
o
x
例1、下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?
解:函数y=f(x)的单调区间有 [-5,-2),[-2,1),[1,3),[3,5]
其中y=f(x)在区间[-5,-2), [1,3)上是减函数,
在区间[-2,1), [3,5] 上是增函数。
例2、物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1由V1,V2∈ (0,+∞)且V10, V2- V1 >0
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
变形
作差
结论
三.判断函数单调性的方法步骤
1 取值:任取x1,x2∈D,且x1(满足三个条件)
2 作差f(x1)-f(x2);
3 变形(通常是因式分解和配方);
4 定号(即判断差f(x1)-f(x2)的正负);
5 下结论(即指出函数f(x)在给定的区间D上的单调性).
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
思考?
思考:画出反比例函数f(x)=1/x的图象.
1 这个函数的定义域是什么?
2 它在定义域I上的单调性怎样?证明你的结论.
证明:函数f(x)=1/x 在(0,+∞)上是减函数。
证明:设x1,x2是(0,+∞)上任意两个实数,且x1f(x1)- f(x2)=
由于x1,x2 得x1x2>0,又由x10
所以f(x1)- f(x2)>0, 即f(x1)> f(x2)
因此 f(x)=1/x 在(0,+∞)上是减函数。
取值
定号
变形
作差
判断
四、归纳小结
函数的单调性一般是先根据图象判断,再利用定义证明.画函数图象通常借助计算机,求函数的单调区间时必须要注意函数的定义域,单调性的证明一般分五步:
取 值 → 作 差 → 变 形 → 定 号 → 下结论
必做: 课本P39 习题1.3(A组)
第1(不需要证明)、 2题.
五、作业
选做: 课本P39 习题1.3(A组) 第3题.
§ 1.3.1 单调性与最大(小)值(一)
——函数的单调性
永昌四中 陈瑞天
*
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
1、观察这三个图象,你能说出图象的特征吗?
2、随x的增大,y的值有什么变化?
探索研究
画出下列函数的图象,观察其变化规律:
1、从左至右图象上升还是下降 ____
2、在区间 ________上,随着x的增大,f(x)的值随着 ______ .
f(x) = x
(-∞,+∞)
增大
上升
1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____.
f(x) = x2
(-∞,0]
(0,+∞)
增大
减小
画出下列函数的图象,观察其变化规律:
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x)=x2 … 16 9 4 1 0 1 4 9 16 …
一、函数单调性定义
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
2.减函数
1、函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
注意:
2 、必须是对于区间D内的任意两个自变量x1,x2;当x1
如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
二.函数的单调性定义
y
o
x
o
y
x
y
o
x
y
o
x
y
o
x
在
增函数
在
减函数
在
增函数
在
减函数
在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数
在(-∞,+∞)是增函数
在(-∞,0)和(0,+∞)是增函数
y
o
x
例1、下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?
解:函数y=f(x)的单调区间有 [-5,-2),[-2,1),[1,3),[3,5]
其中y=f(x)在区间[-5,-2), [1,3)上是减函数,
在区间[-2,1), [3,5] 上是增函数。
例2、物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
变形
作差
结论
三.判断函数单调性的方法步骤
1 取值:任取x1,x2∈D,且x1
2 作差f(x1)-f(x2);
3 变形(通常是因式分解和配方);
4 定号(即判断差f(x1)-f(x2)的正负);
5 下结论(即指出函数f(x)在给定的区间D上的单调性).
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
思考?
思考:画出反比例函数f(x)=1/x的图象.
1 这个函数的定义域是什么?
2 它在定义域I上的单调性怎样?证明你的结论.
证明:函数f(x)=1/x 在(0,+∞)上是减函数。
证明:设x1,x2是(0,+∞)上任意两个实数,且x1
由于x1,x2 得x1x2>0,又由x1
所以f(x1)- f(x2)>0, 即f(x1)> f(x2)
因此 f(x)=1/x 在(0,+∞)上是减函数。
取值
定号
变形
作差
判断
四、归纳小结
函数的单调性一般是先根据图象判断,再利用定义证明.画函数图象通常借助计算机,求函数的单调区间时必须要注意函数的定义域,单调性的证明一般分五步:
取 值 → 作 差 → 变 形 → 定 号 → 下结论
必做: 课本P39 习题1.3(A组)
第1(不需要证明)、 2题.
五、作业
选做: 课本P39 习题1.3(A组) 第3题.
