第二章 基本初等复习

(共22张PPT)
第二章复习2
永昌四中
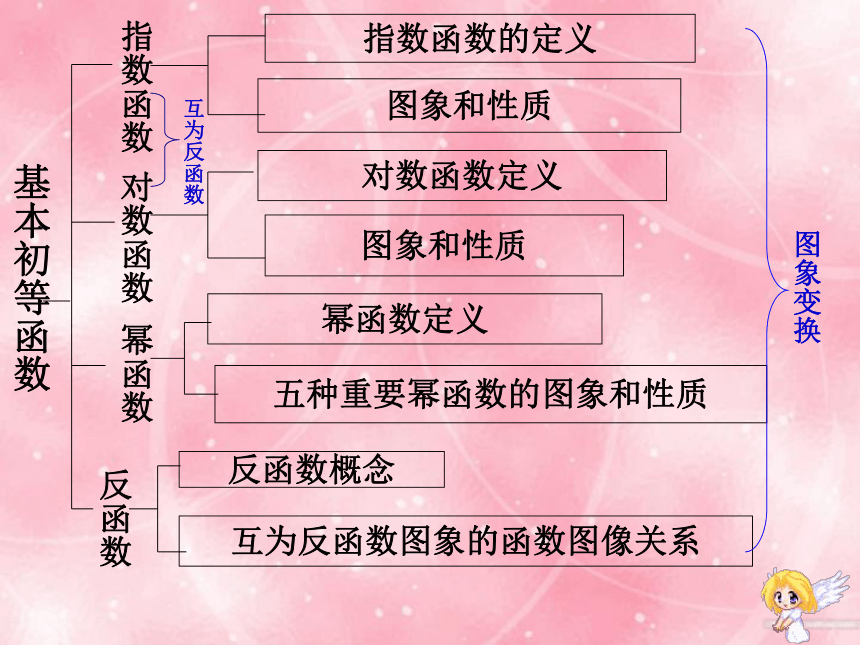
基本初等函数
指数函数
指数函数的定义
图象和性质
对数函数
对数函数定义
图象和性质
幂函数
幂函数定义
五种重要幂函数的图象和性质
反函数概念
互为反函数图象的函数图像关系
反函数
互为反函数
图象变换
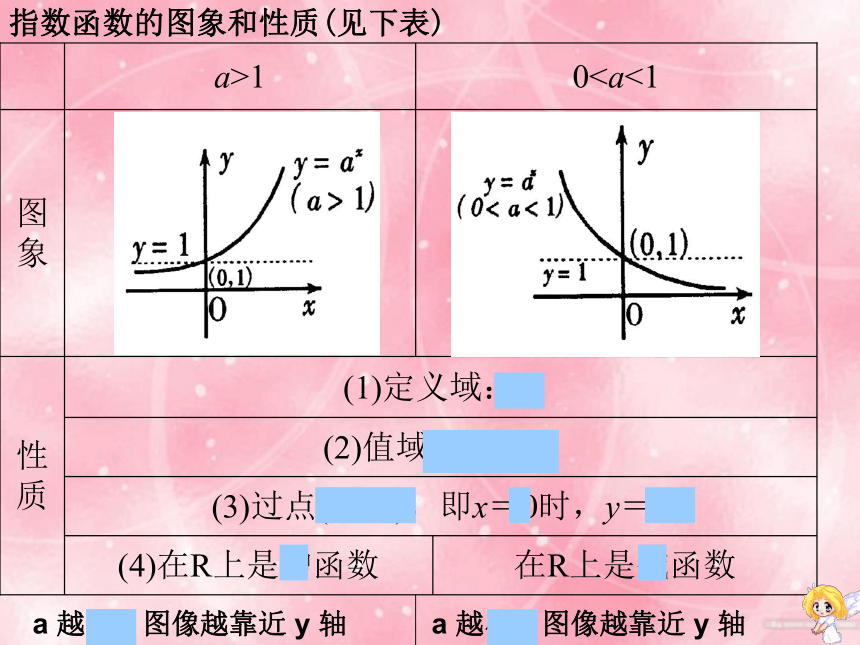
指数函数定义：
函数 y=ax （a>0,a≠1）叫做指数函数,其中x是自变量，函数的定义域为R
①若a=0，则当x≤0时，
②若a<0，对于x的某些数值，可能使
③若a=1，则对于任何x
R，
=1，是一个常量，没有研究的必要性.
指数函数的图象和性质(见下表)
在R上是减函数
(4)在R上是增函数
(3)过点(0，1)，即x＝0时，y＝1
(2)值域(0，＋∞)
(1)定义域：R
a>1
0性质
图象
a 越小，图像越靠近 y 轴
a 越大，图像越靠近 y 轴
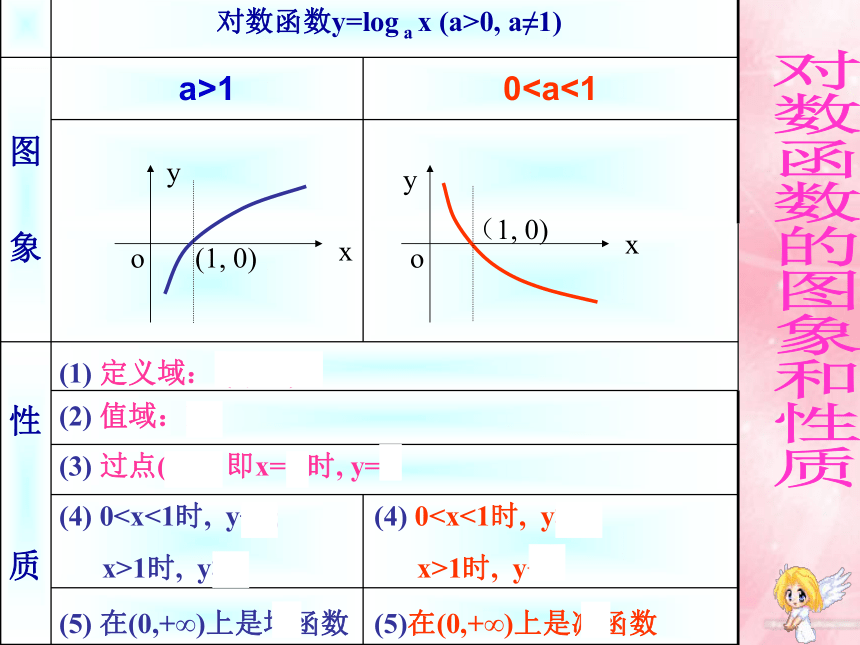
1.对数函数：
一般地，我们把函数 （a＞0且a≠1）叫做对数函数，其中x是自变量，函数的定义
域是（0，+∞）．
，
注意：
①对数函数的定义与指数函数类似，都是形式定义，注意辨别．如： ，
都不是对数函数，而只能称其为对数型函数．
②对数函数对底数的限制：
图
象
a>1 0性
质
对数函数y=log a x (a>0, a≠1)
(4) 0x>1时, y>0
(4) 00;
x>1时, y<0
(3) 过点(1,0), 即x=1 时, y=0
(1) 定义域： (0,+∞)
(2) 值域：R
x
y
o
(1, 0)
x
y
o
（1, 0)
(5)在(0,+∞)上是减函数
(5) 在(0,+∞)上是增函数
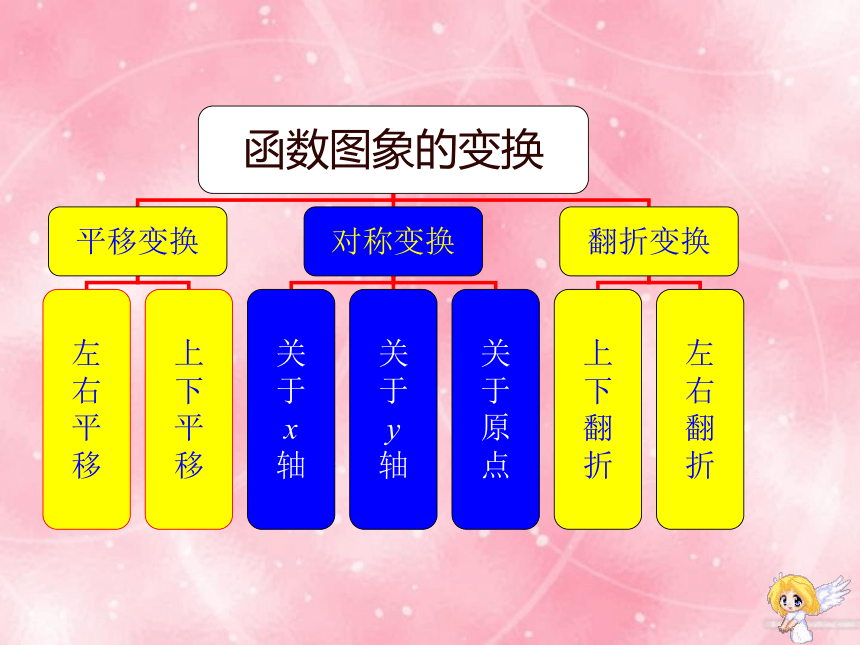
函数图象的变换
平移变换
对称变换
翻折变换
左
右
平
移
上
下
平
移
关
于
x
轴
关
于
y
轴
关
于
原
点
上
下
翻
折
左
右
翻
折
平
移
变
换
y = f(x)
的图象
y = f(x + h)
的 图 象
左移 h (h>0)
个 单 位
y = f(x - h)
的 图 象
y = f(x)
的图象
右移 h (h>0)
个 单 位
平
移
变
换
y = f(x)
的图象
上移 k (k>0)
个 单 位
y = f(x)
的图象
下移 k (k>0)
个 单 位
y = f(x)+k
y = f(x) - k
对
称
变
换
y = f(x)
的图象
y = f( -x )
的 图 象
关于 y 轴
对 称
y = f(x)
的图象
y = - f(x)
的 图 象
关于 x 轴
对 称
y = f(x)
的图象
y = - f( -x )
的 图 象
关于原点
对 称
翻
折
变
换
y = f(x)
的图象
y = f(|x|)
的图象
将y = f(x)在 y 轴右边的图
象保留，右边的图象以 y 轴
为对称轴翻折到左边可得到
y =f(|x|) 的图象
翻
折
变
换
y = f(x)
的图象
将y = f(x)在 x 轴上方的图
象保留，下方的图象以 x 轴
为对称轴翻折到上方可得到
y =|f(x)|的图象
y =|f( x )|
的图象
原来函数y= f(x )与反函数y=f-1(x)的定义域与值域互换
1.反函数与原来函数的联系
2、求反函数的步骤：
（1）写出原来函数的定义域和值域
（2）由y=f（x）反解得x=f-1(y)
（3）把x、y互换
（4）写出反函数的解析式与定义域
并不是所有的函数都具有反函数，
只有满足一一映射的函数才具有反函数
关于反函数的三条性质：
1，互为反函数的函数图像间关于直线 对称。
即原来函数图像过点（a,b），则反函数图像过点
（b,a）
3，
的值即为方程
的值即为方程
2，
（1）以幂的底为自变量;
（2）指数为常数；
（3）幂前的系数为1
幂函数的特点
幂函数的定义：
一般地函数
叫做幂函数
幂函数与指数函数有什么区别？
幂函数的底数为自变量，指数是常数，
而指数函数底数是常数，指数是自变量
定义域
值 域
奇偶性
单调性
定 点
五种重要幂函数的性质
幂函数的图象特征和性质：
1. >0时,
(1)图象都经过点（0，0）和（1，1）；
(2)图象在第一象限是上升的,即在 上是增 函数.
(3)图象呈“抛物线”型的弧.
2. <0时
(1)图象都经过点（1，1）；
(2)图象在第一象限是下降的,且向右无限接近X
轴，向上无限接近Y轴,即在 上是
减函数.
(3)图象呈“双曲线”型的弧.
在直线x=1右侧,幂指数越大,图象越高,即越远
离x轴;即x>1时,当函数的自变量相等时,幂指
数越大,函数值越大
4，在直线x=1左侧，幂指数越大,图象越低,即越
靠近x轴;即0指数越大,函数值越小
第一象限内幂函数图像的特点
分析：
f(m+n)=2
例1
例2 已知函数
（1）求f(x)的定义域与值域；
（2）判断f(x)的奇偶性
（3）讨论f(x)的单调性
（4）求f(x)的反函数
奇函数
范例讲解
例3、已知
（1）求定义域；（2）讨论函数的单调区间
解 （1）由
函数在 上是增函数
函数在 上也是增函数
(2)
布置作业
1.
2.
求其定义域
3.