北师大版数学八年级上册6.4 数据的离散程度 课件(第1课时 33张)
文档属性
| 名称 | 北师大版数学八年级上册6.4 数据的离散程度 课件(第1课时 33张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:43:13 | ||
图片预览






文档简介
6.4 数据的离散程度
(第1课时)
导入新知
现要从甲,乙两名射击选手中挑选一名射击选手参加比赛.若你是教练,你认为挑选哪一位比较合适?
教练的烦恼
?
导入新知
甲,乙两名射击选手的测试成绩统计如下:
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
8
8
9
乙命中环数
10
6
10
6
8
1. 理解极差、方差、标准差的概念、意义并掌握其计算方法.
2. 会计算一组数据的方差.
素养目标
3. 能利用极差、方差、标准差分析数据,做出决策.
探究 为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分.
某外贸公司要出口一批规格为75 g的鸡腿,现有2个厂家提供货源,它们的价格相同,鸡腿品质也相近.
探究新知
知识点
极差、方差、标准差的概念
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿,质量(单位:g)如下:
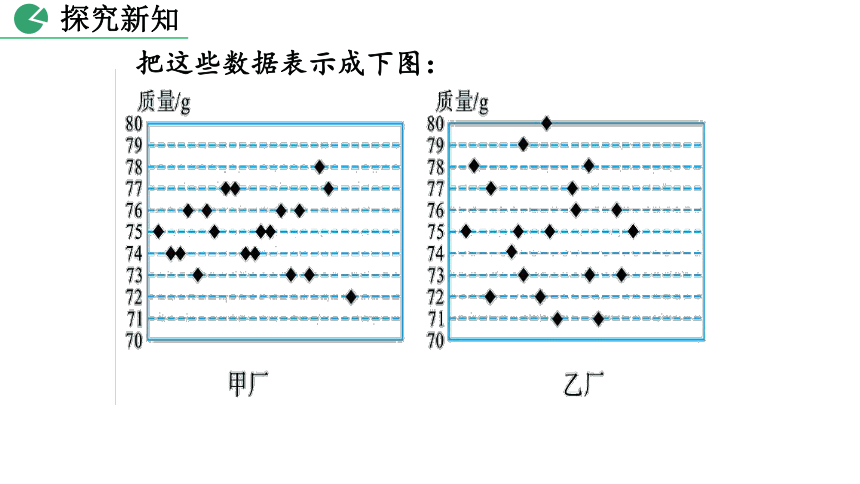
甲厂:75 74 74 76 73 76 75 77 77 74
74 75 75 76 73 76 73 78 77 72
乙厂:75 78 72 77 74 75 73 79 72 75
80 71 76 77 73 78 71 76 73 75
把这些数据表示成下图:
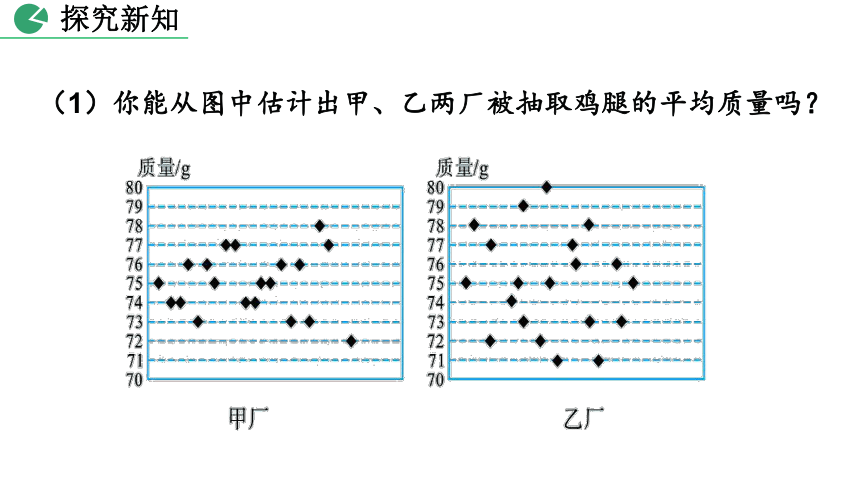
探究新知
(1)你能从图中估计出甲、乙两厂被抽取鸡腿的平均质量吗?
探究新知
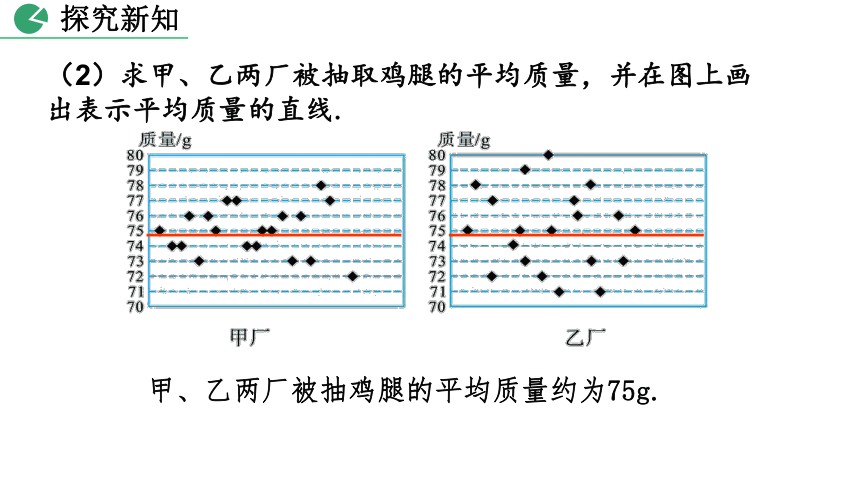
(2)求甲、乙两厂被抽取鸡腿的平均质量,并在图上画出表示平均质量的直线.
甲、乙两厂被抽鸡腿的平均质量约为75g.
探究新知
(3)从甲厂抽取的这20只鸡腿质量的最大值是多少?最小值又是多少?它们相差几克?乙厂呢?
(4)如果只考虑鸡腿的规格,你认为外贸公司应购买哪个厂家的鸡腿?
解:甲厂:最大值78g,最小值72g,相差6g;
乙厂:最大值80g,最小值71g,相差9g;
解:平均质量只能反映总体的集中趋势,并不能反映个体的变化情况.从图中看,甲厂的产品更符合要求.
探究新知
现实生活中,除了关心数据的“平均水平”外,人们还关注数据的离散程度,即它们相对于平均水平的偏离情况.极差就是刻画数据离散程度的一个统计量.
极差是指一组数据中最大数据与最小数据的差.
极差越大,偏离平均数越大,产品的质量(性能)越不稳定.
探究新知
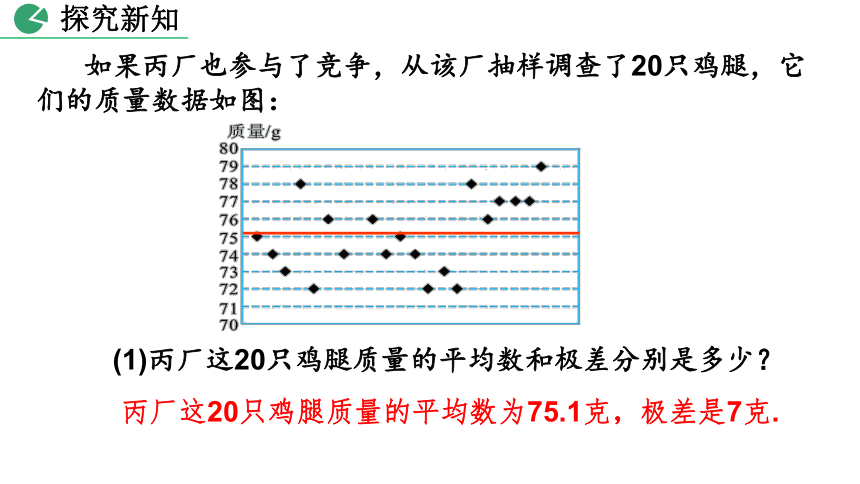
如果丙厂也参与了竞争,从该厂抽样调查了20只鸡腿,它们的质量数据如图:
(1)丙厂这20只鸡腿质量的平均数和极差分别是多少?
丙厂这20只鸡腿质量的平均数为75.1克,极差是7克.
探究新知
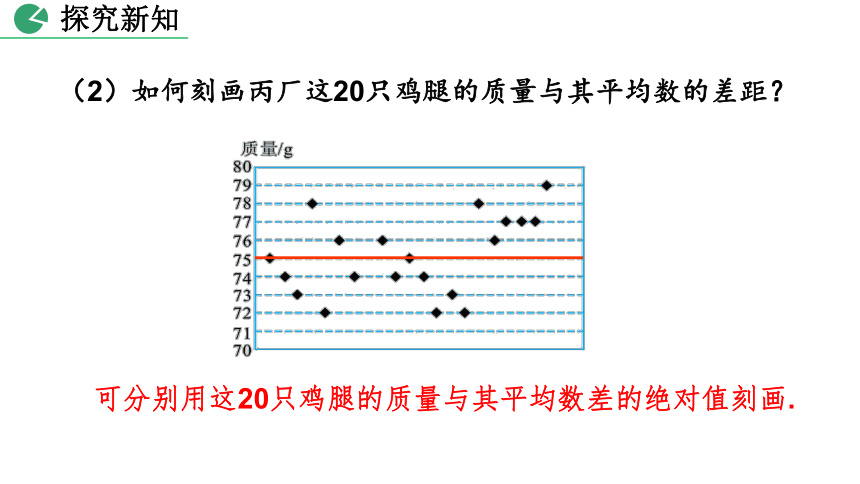
(2)如何刻画丙厂这20只鸡腿的质量与其平均数的差距?
可分别用这20只鸡腿的质量与其平均数差的绝对值刻画.
探究新知
(3)分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.
甲厂的差距依次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
探究新知
(4)在甲、丙两厂中,你认为哪个厂的鸡腿质量更符合要求?为什么?
差距和较小
甲厂的差距依次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
差距和
较大
探究新知
数学上,数据的离散程度还可以用方差或标准差来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
其中 是x1,x2,……,xn的平均数,s2是方差,而标准差就是方差的算术平方根.
探究新知
计算出从甲厂抽取的20只鸡腿质量的方差?
甲厂20只鸡腿质量的方差:
2.5.
解:甲厂20只鸡腿的平均质量:
=2.5.
或
探究新知
=75(g).
甲厂:75 74 74 76 73 76 75 77 77 74
74 75 75 76 73 76 73 78 77 72
例
(1)计算出从丙厂抽取的20只鸡腿质量的方差?
(2)根据计算的结果,你认为甲、丙两厂的产品哪个更符合规格?
丙厂:
解:(1)
(2)因为S2甲< S2丙 ,所以甲厂更符合规定.
探究新知
做一做
4.2.
S2丙 =
甲团
163
164
164
165
165
166
166
167
乙团
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
例 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
探究新知
素养考点
利用加权平均数方差解答实际问题
解:甲、乙两团演员的平均身高分别是
探究新知
方法一:
方差分别是
方法二:
解: 取 a = 165
甲芭蕾舞团数据为: -2,-1, -1, 0,0,1,1,2
乙芭蕾舞团数据为: -2,0,0,1,1,2,3,3
求两组新数据方差.
探究新知
探究新知
方法点拨
求一组较大数据的方差,有如下简便计算方法:
1.任取一个基准数a;
2.将原数据减去a,得到一组新数据;
3.求新数据的方差.
甲、乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;
乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
∴乙台编织机出的产品的波动性较小.
巩固练习
∵
解:
变式训练
1.打开计算器,依次按以下键进入统计状态.
2.按键输入数据2,3,4;
3.进入统计计算指令:
按 则显示改组数据的平均数;
按 则显示改组数据的标准差.
使用计算器说明:
探究新知
(2019?宁波)去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数 (单位:千克)及方差S2,如表所示:
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A.甲 B.乙 C.丙 D.丁
B
{5940675A-B579-460E-94D1-54222C63F5DA}
甲
乙
丙
丁
24
24
23
20
S2
2.1
1.9
2
1.9
连接中考
1.样本方差的作用是( )
A. 表示总体的平均水平 B.表示样本的平均水平
C.准确表示总体的波动大小 D.表示样本的波动大小
D
2.一组数据2,0,1,x,3的平均数是2,则这组数据的方差是( )
A. 2 B. 4
C. 1 D. 3
A
基础巩固题
课堂检测
3.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B. 乙 C. 丙 D. 丁
A
课堂检测
基础巩固题
4.已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A. 1 B. 2
C. 3 D. 4
D
课堂检测
基础巩固题
在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学
70
95
75
95
90
英语
80
85
90
85
85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学 110; ②英语 10
建议:英语较稳定但要提高; 数学不够稳定有待努力进步!
课堂检测
能力提升题
为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩
76
84
90
84
81
87
88
81
85
84
乙的成绩
82
86
87
90
79
81
93
90
74
78
拓广探索题
课堂检测
(1)填写下表:
同学
平均成绩
中位数
众数
方差
85分以上的频率
甲
84
84
0.3
乙
84
84
34
84
90
0.5
14.4
(2)利用以上信息,请从不同的角度对甲、乙两名同学 的成绩进行评价.
课堂检测
拓广探索题
解:从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4, s2乙=34,甲的成绩比乙相对稳定;
从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好.
课堂检测
拓广探索题
1.极差的定义:
极差是指一组数据中最大数据与最小数据的差.
2.方差的定义:
方差是各个数据与平均数之差的平方的平均数,即
其中,x是x1,x2 ,… ,xn的平均数,是方差.
3.标准差的定义:
标准差是方差的算术平方根.
4.数据的稳定性:
一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第1课时)
导入新知
现要从甲,乙两名射击选手中挑选一名射击选手参加比赛.若你是教练,你认为挑选哪一位比较合适?
教练的烦恼
?
导入新知
甲,乙两名射击选手的测试成绩统计如下:
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
8
8
9
乙命中环数
10
6
10
6
8
1. 理解极差、方差、标准差的概念、意义并掌握其计算方法.
2. 会计算一组数据的方差.
素养目标
3. 能利用极差、方差、标准差分析数据,做出决策.
探究 为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分.
某外贸公司要出口一批规格为75 g的鸡腿,现有2个厂家提供货源,它们的价格相同,鸡腿品质也相近.
探究新知
知识点
极差、方差、标准差的概念
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿,质量(单位:g)如下:
甲厂:75 74 74 76 73 76 75 77 77 74
74 75 75 76 73 76 73 78 77 72
乙厂:75 78 72 77 74 75 73 79 72 75
80 71 76 77 73 78 71 76 73 75
把这些数据表示成下图:
探究新知
(1)你能从图中估计出甲、乙两厂被抽取鸡腿的平均质量吗?
探究新知
(2)求甲、乙两厂被抽取鸡腿的平均质量,并在图上画出表示平均质量的直线.
甲、乙两厂被抽鸡腿的平均质量约为75g.
探究新知
(3)从甲厂抽取的这20只鸡腿质量的最大值是多少?最小值又是多少?它们相差几克?乙厂呢?
(4)如果只考虑鸡腿的规格,你认为外贸公司应购买哪个厂家的鸡腿?
解:甲厂:最大值78g,最小值72g,相差6g;
乙厂:最大值80g,最小值71g,相差9g;
解:平均质量只能反映总体的集中趋势,并不能反映个体的变化情况.从图中看,甲厂的产品更符合要求.
探究新知
现实生活中,除了关心数据的“平均水平”外,人们还关注数据的离散程度,即它们相对于平均水平的偏离情况.极差就是刻画数据离散程度的一个统计量.
极差是指一组数据中最大数据与最小数据的差.
极差越大,偏离平均数越大,产品的质量(性能)越不稳定.
探究新知
如果丙厂也参与了竞争,从该厂抽样调查了20只鸡腿,它们的质量数据如图:
(1)丙厂这20只鸡腿质量的平均数和极差分别是多少?
丙厂这20只鸡腿质量的平均数为75.1克,极差是7克.
探究新知
(2)如何刻画丙厂这20只鸡腿的质量与其平均数的差距?
可分别用这20只鸡腿的质量与其平均数差的绝对值刻画.
探究新知
(3)分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.
甲厂的差距依次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
探究新知
(4)在甲、丙两厂中,你认为哪个厂的鸡腿质量更符合要求?为什么?
差距和较小
甲厂的差距依次是:
0 1 1 1 2
1 0 2 2 1
1 0 0 1 2
1 2 3 2 3
丙厂的差距依次是:
0.1 1.1 2.1 2.9 3.1 0.9 1.1 0.9 1.1 0.1 1.1 3.1 2.1 3.1 2.9 0.9 1.9 1.9 1.9 3.9
甲厂
丙厂
差距和
较大
探究新知
数学上,数据的离散程度还可以用方差或标准差来刻画.
方差是各个数据与平均数之差的平方的平均数,
即
一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
其中 是x1,x2,……,xn的平均数,s2是方差,而标准差就是方差的算术平方根.
探究新知
计算出从甲厂抽取的20只鸡腿质量的方差?
甲厂20只鸡腿质量的方差:
2.5.
解:甲厂20只鸡腿的平均质量:
=2.5.
或
探究新知
=75(g).
甲厂:75 74 74 76 73 76 75 77 77 74
74 75 75 76 73 76 73 78 77 72
例
(1)计算出从丙厂抽取的20只鸡腿质量的方差?
(2)根据计算的结果,你认为甲、丙两厂的产品哪个更符合规格?
丙厂:
解:(1)
(2)因为S2甲< S2丙 ,所以甲厂更符合规定.
探究新知
做一做
4.2.
S2丙 =
甲团
163
164
164
165
165
166
166
167
乙团
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
例 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
探究新知
素养考点
利用加权平均数方差解答实际问题
解:甲、乙两团演员的平均身高分别是
探究新知
方法一:
方差分别是
方法二:
解: 取 a = 165
甲芭蕾舞团数据为: -2,-1, -1, 0,0,1,1,2
乙芭蕾舞团数据为: -2,0,0,1,1,2,3,3
求两组新数据方差.
探究新知
探究新知
方法点拨
求一组较大数据的方差,有如下简便计算方法:
1.任取一个基准数a;
2.将原数据减去a,得到一组新数据;
3.求新数据的方差.
甲、乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;
乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
∴乙台编织机出的产品的波动性较小.
巩固练习
∵
解:
变式训练
1.打开计算器,依次按以下键进入统计状态.
2.按键输入数据2,3,4;
3.进入统计计算指令:
按 则显示改组数据的平均数;
按 则显示改组数据的标准差.
使用计算器说明:
探究新知
(2019?宁波)去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数 (单位:千克)及方差S2,如表所示:
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A.甲 B.乙 C.丙 D.丁
B
{5940675A-B579-460E-94D1-54222C63F5DA}
甲
乙
丙
丁
24
24
23
20
S2
2.1
1.9
2
1.9
连接中考
1.样本方差的作用是( )
A. 表示总体的平均水平 B.表示样本的平均水平
C.准确表示总体的波动大小 D.表示样本的波动大小
D
2.一组数据2,0,1,x,3的平均数是2,则这组数据的方差是( )
A. 2 B. 4
C. 1 D. 3
A
基础巩固题
课堂检测
3.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B. 乙 C. 丙 D. 丁
A
课堂检测
基础巩固题
4.已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A. 1 B. 2
C. 3 D. 4
D
课堂检测
基础巩固题
在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学
70
95
75
95
90
英语
80
85
90
85
85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学 110; ②英语 10
建议:英语较稳定但要提高; 数学不够稳定有待努力进步!
课堂检测
能力提升题
为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩
76
84
90
84
81
87
88
81
85
84
乙的成绩
82
86
87
90
79
81
93
90
74
78
拓广探索题
课堂检测
(1)填写下表:
同学
平均成绩
中位数
众数
方差
85分以上的频率
甲
84
84
0.3
乙
84
84
34
84
90
0.5
14.4
(2)利用以上信息,请从不同的角度对甲、乙两名同学 的成绩进行评价.
课堂检测
拓广探索题
解:从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4, s2乙=34,甲的成绩比乙相对稳定;
从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好.
课堂检测
拓广探索题
1.极差的定义:
极差是指一组数据中最大数据与最小数据的差.
2.方差的定义:
方差是各个数据与平均数之差的平方的平均数,即
其中,x是x1,x2 ,… ,xn的平均数,是方差.
3.标准差的定义:
标准差是方差的算术平方根.
4.数据的稳定性:
一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
