北师大版九年级上册 第三章 概率的进一步认识 小结与复习 课件(33张)
文档属性
| 名称 | 北师大版九年级上册 第三章 概率的进一步认识 小结与复习 课件(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
第三章
概率的进一步认识
小结与复习
九年级数学教学课件(北师版)
要点梳理
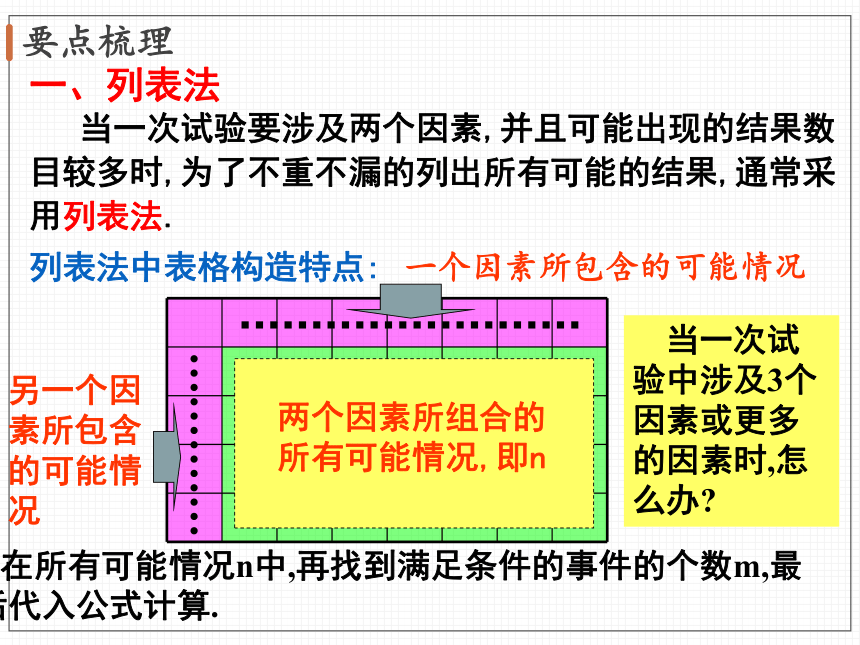
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办?
一、列表法
要点梳理
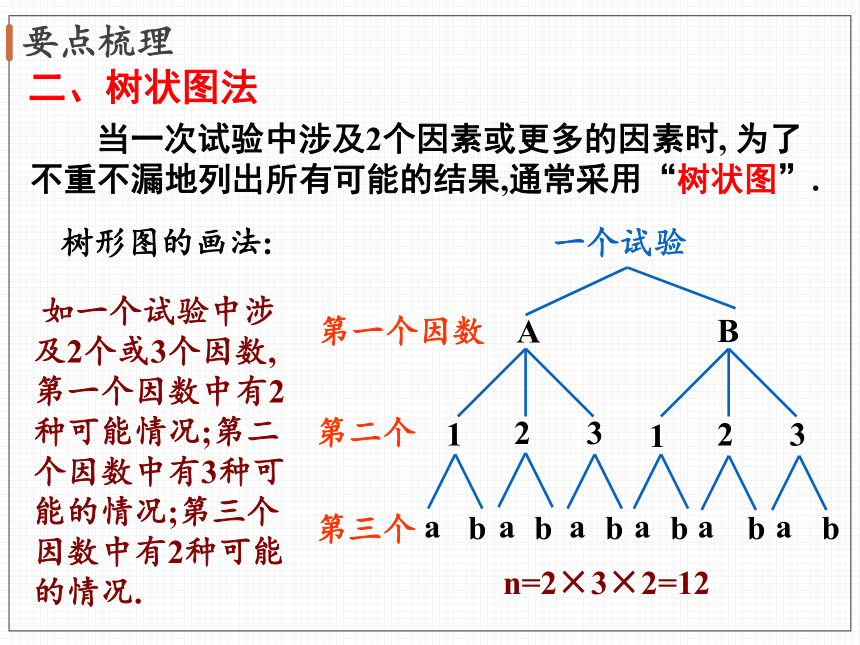
当一次试验中涉及2个因素或更多的因素时,
为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
二、树状图法
要点梳理
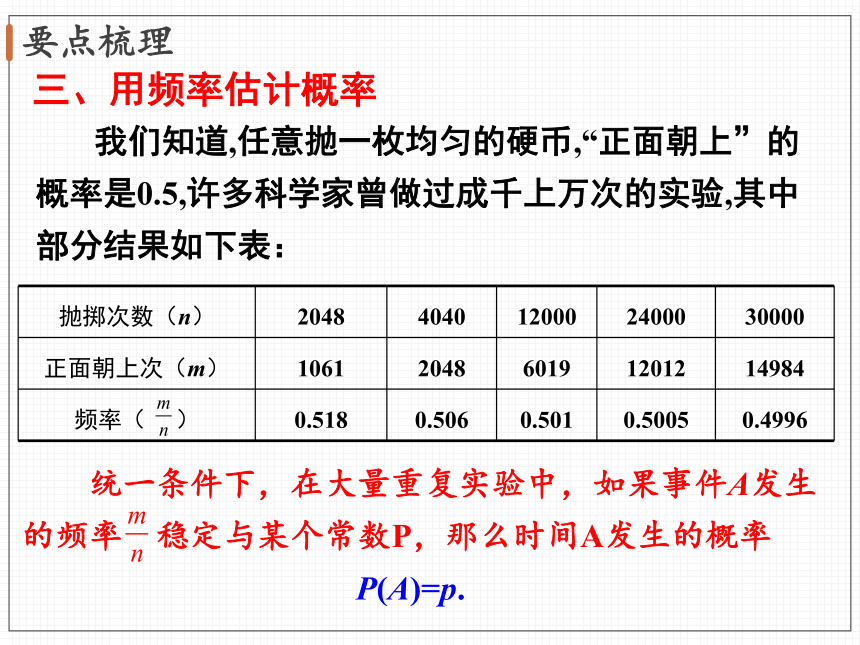
我们知道,任意抛一枚均匀的硬币,“正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
抛掷次数(n)
2048
4040
12000
24000
30000
正面朝上次(m)
1061
2048
6019
12012
14984
频率(
)
0.518
0.506
0.501
0.5005
0.4996
统一条件下,在大量重复实验中,如果事件A发生的频率
稳定与某个常数P,那么时间A发生的概率
P(A)=p.
三、用频率估计概率
考点讲练
核心知识点一
用列举法求概率
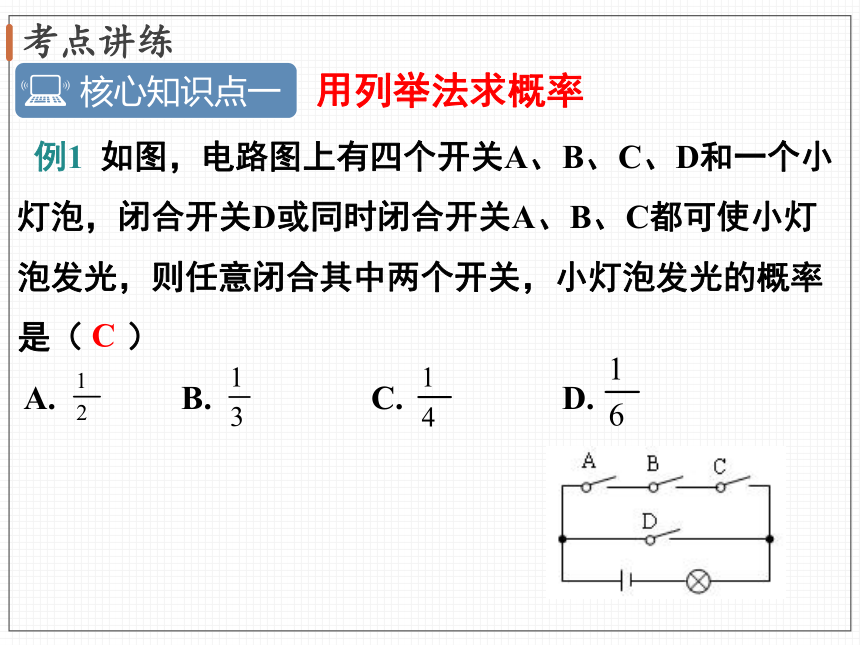
例1
如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是(
)
A.
B.
C.
D.
C
考点讲练
例2
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象经过
二、三、四象限的概率.
考点讲练
解:(1)P(k为负数)=
.
【解析】(1)因为-1,-2,3中有两个负数,故k为负数的概率为
;
(2)由于一次函数y=kx+b的图象经过二、三、四象限时,k,b均为负数,
所以在画树形图列举出k、b取值的所有情况后,从中找出所有k、b均为负数的情况,即可得出答案.
考点讲练
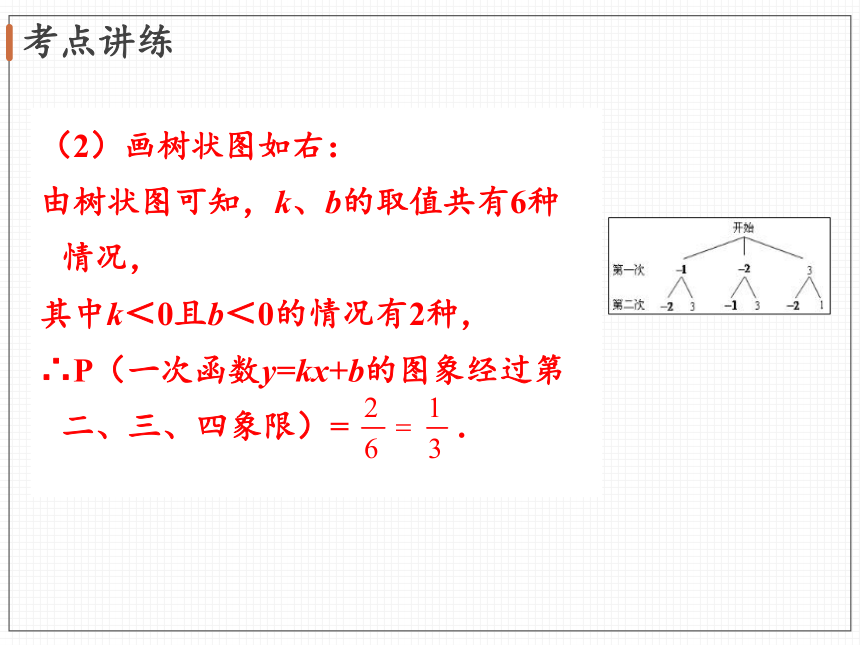
(2)画树状图如右:
由树状图可知,k、b的取值共有6种情况,
其中k<0且b<0的情况有2种,
∴P(一次函数y=kx+b的图象经过第二、三、四象限)=
.
考点讲练
1.
一个袋中装有2个黑球3个白球,这些球除颜色外,大小、形状、质地完全相同,在看不到球的情况下,随机的从这个袋子中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
A
针对训练
考点讲练
核心知识点二
用树状图或表格法求概率
例3
在中央电视台《星光大道》2015年度冠军总决赛中,甲、乙、丙三位评委对选手的综合表现,分别给出“待定”或“通过”的结论.
(1)写出三位评委给出A选手的所有可能的结果;
(2)对于选手A,只有甲、乙两位评委给出相同结果的概率是多少?
考点讲练
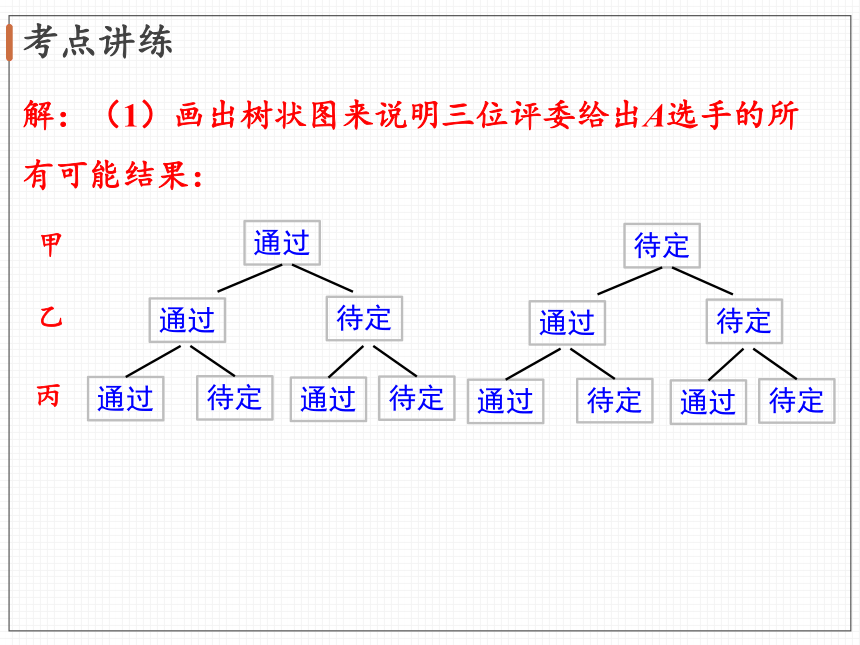
解:(1)画出树状图来说明三位评委给出A选手的所有可能结果:
通过
通过
待定
通过
待定
通过
待定
甲
乙
丙
待定
通过
待定
通过
待定
通过
待定
考点讲练
(2)由上图可知三位评委给出A选手的所有可能的结果共有8种.
对于选手A,
“只有甲、乙两位评委给出相同结果”有2种,即“通过-通过-待定”
“待定-待定-通过”,所以对于选手A,
“只有甲、乙两位评委给出相同结果”的概率是
.
(2)对于选手A,只有甲、乙两位评委给出相同结果的概率是多少?
考点讲练
这个游戏对小亮和小明公平吗?
例4
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”.如果你是小亮,你愿意接受这个游戏的规则吗?
为什么?
考点讲练
1
2
3
4
5
6
1
2
3
4
5
6
红
桃
黑桃
解:这个游戏不公平,理由如下:
列表:
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
由表中可以看出,在两堆牌中分别取一张,它可能出现的结果有36个,它们出现的可能性相等.
考点讲练
因为P(A)
<
P(B),所以如果我是小亮,我不愿
意接受这个游戏的规则.
满足两张牌的数字之积为奇数(记为事件A)
的有9种情况,所以
满足两张牌的数字之积为偶数(记为事件B)
的有27种情况,所以
考点讲练
用画树状图或列表分析是求概率的常用方法:
1.当事件要经过多个步骤完成是,用画树状图法求事件的概率很有效;
2.一次试验要涉及两个因素,并且可能出现的结果数目较多时,通常采用列表法分析所有等可能的结果;当结果要求进行数的和、积等有关运算时,用列表法显得更加清晰、明确.
方法总结
考点讲练
针对训练
2.
一个袋中装有2个黑球3个白球,这些球除颜色外,大小、形状、质地完全相同,在看不到球的情况下,随机的从这个袋子中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
A
考点讲练
3.如图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到红色部分的概率.
图①
图②
解:图①,
图②,设圆的半径为a,则
考点讲练
4.
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象
经过二、三、四象限的概率.
考点讲练
【解析】(1)因为-1,-2,3中有两个负数,故k为负数的概率为
;
(2)由于一次函数y=kx+b的图象经过二、三、四象限时,k,b均为负数,所以在画树形图列举出k、b取值的所有情况后,从中找出所有k、b均为负数的情况,即可得出答案.
考点讲练
(2)画树状图如下:
由树状图可知,k、b的取值共有6种情况,其中k<0且b<0的情况有2种,
∴P=
解:(1)P(k为负数)=
.
开始
-1
3
-2
-2
3
-1
3
-2
1
考点讲练
核心知识点三
用频率估计概率
例5
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是(
)
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
考点讲练
例6
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数最有可能是(
)
A.24个
B.18个
C.16个
D.6个
C
考点讲练
针对训练
5.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球.如果口袋中装有3个红球且摸到红球的概率为
,那么口袋中球的总个数为_____.
解析:设口袋中球的总个数为x,
则摸到红球的概率为
,
所以x=15.
15
考点讲练
核心知识点四
用概率作决策
例6
在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
考点讲练
解:(1)列表如下
6
7
8
2
(6,2)
(7,2)
(8,2)
4
(6,4)
(7,4)
(8,4)
6
(6,6)
(7,6)
(8,6)
卡片
小球
共有9种等可能结果;
考点讲练
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
规则1:P(小红赢)=
;
规则2:P(小红赢)=
∵
,
∴小红选择规则1.
考点讲练
针对训练
6.A、B两个小型超市举行有奖促销活动,顾客每购满20元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同.规则是:
①A超市把转盘甲等分成4个扇形区域、B超市把转盘乙等分成3个扇形区域,并标上了数字(如图所示);
②顾客第一回转动转盘要转两次,第一次与第二次分别停止
后指针所指数字之和为奇数时
就获奖(若指针停在等分线上,
那么重转一次,直到指针指向
某一份为止).
1
1
2
2
3
3
4
甲
乙
考点讲练
解:(1)列表格如下:
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
第一回
第二回
甲转盘
共有16种等可能结果,其中中奖的有8种;
∴P(甲)=
(1)利用树形图或列表法分别求出A、B两超市顾客一回转盘获奖的概率;
考点讲练
1
2
3
1
2
3
4
2
3
4
5
3
4
5
6
第一回
第二回
乙转盘
∴P(乙)=
共有9种等可能结果,其中中奖的有4种;
考点讲练
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?说明理由.
(2)选甲超市.理由如下:
∵P(甲)>P(乙),
∴选甲超市.
知识小结
概率的进一步认识
简单的随机事件
复杂的随机事件
具有等可能性
不具有等可能性
树状图
列表
试验法
摸拟试验
理论计算
试验估算
概率定义
谢谢欣赏
THANK
YOU
FOR
LISTENING
第三章
概率的进一步认识
小结与复习
九年级数学教学课件(北师版)
要点梳理
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办?
一、列表法
要点梳理
当一次试验中涉及2个因素或更多的因素时,
为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
二、树状图法
要点梳理
我们知道,任意抛一枚均匀的硬币,“正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
抛掷次数(n)
2048
4040
12000
24000
30000
正面朝上次(m)
1061
2048
6019
12012
14984
频率(
)
0.518
0.506
0.501
0.5005
0.4996
统一条件下,在大量重复实验中,如果事件A发生的频率
稳定与某个常数P,那么时间A发生的概率
P(A)=p.
三、用频率估计概率
考点讲练
核心知识点一
用列举法求概率
例1
如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是(
)
A.
B.
C.
D.
C
考点讲练
例2
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象经过
二、三、四象限的概率.
考点讲练
解:(1)P(k为负数)=
.
【解析】(1)因为-1,-2,3中有两个负数,故k为负数的概率为
;
(2)由于一次函数y=kx+b的图象经过二、三、四象限时,k,b均为负数,
所以在画树形图列举出k、b取值的所有情况后,从中找出所有k、b均为负数的情况,即可得出答案.
考点讲练
(2)画树状图如右:
由树状图可知,k、b的取值共有6种情况,
其中k<0且b<0的情况有2种,
∴P(一次函数y=kx+b的图象经过第二、三、四象限)=
.
考点讲练
1.
一个袋中装有2个黑球3个白球,这些球除颜色外,大小、形状、质地完全相同,在看不到球的情况下,随机的从这个袋子中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
A
针对训练
考点讲练
核心知识点二
用树状图或表格法求概率
例3
在中央电视台《星光大道》2015年度冠军总决赛中,甲、乙、丙三位评委对选手的综合表现,分别给出“待定”或“通过”的结论.
(1)写出三位评委给出A选手的所有可能的结果;
(2)对于选手A,只有甲、乙两位评委给出相同结果的概率是多少?
考点讲练
解:(1)画出树状图来说明三位评委给出A选手的所有可能结果:
通过
通过
待定
通过
待定
通过
待定
甲
乙
丙
待定
通过
待定
通过
待定
通过
待定
考点讲练
(2)由上图可知三位评委给出A选手的所有可能的结果共有8种.
对于选手A,
“只有甲、乙两位评委给出相同结果”有2种,即“通过-通过-待定”
“待定-待定-通过”,所以对于选手A,
“只有甲、乙两位评委给出相同结果”的概率是
.
(2)对于选手A,只有甲、乙两位评委给出相同结果的概率是多少?
考点讲练
这个游戏对小亮和小明公平吗?
例4
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”.如果你是小亮,你愿意接受这个游戏的规则吗?
为什么?
考点讲练
1
2
3
4
5
6
1
2
3
4
5
6
红
桃
黑桃
解:这个游戏不公平,理由如下:
列表:
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
由表中可以看出,在两堆牌中分别取一张,它可能出现的结果有36个,它们出现的可能性相等.
考点讲练
因为P(A)
<
P(B),所以如果我是小亮,我不愿
意接受这个游戏的规则.
满足两张牌的数字之积为奇数(记为事件A)
的有9种情况,所以
满足两张牌的数字之积为偶数(记为事件B)
的有27种情况,所以
考点讲练
用画树状图或列表分析是求概率的常用方法:
1.当事件要经过多个步骤完成是,用画树状图法求事件的概率很有效;
2.一次试验要涉及两个因素,并且可能出现的结果数目较多时,通常采用列表法分析所有等可能的结果;当结果要求进行数的和、积等有关运算时,用列表法显得更加清晰、明确.
方法总结
考点讲练
针对训练
2.
一个袋中装有2个黑球3个白球,这些球除颜色外,大小、形状、质地完全相同,在看不到球的情况下,随机的从这个袋子中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
A
考点讲练
3.如图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到红色部分的概率.
图①
图②
解:图①,
图②,设圆的半径为a,则
考点讲练
4.
如图所示,有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象
经过二、三、四象限的概率.
考点讲练
【解析】(1)因为-1,-2,3中有两个负数,故k为负数的概率为
;
(2)由于一次函数y=kx+b的图象经过二、三、四象限时,k,b均为负数,所以在画树形图列举出k、b取值的所有情况后,从中找出所有k、b均为负数的情况,即可得出答案.
考点讲练
(2)画树状图如下:
由树状图可知,k、b的取值共有6种情况,其中k<0且b<0的情况有2种,
∴P=
解:(1)P(k为负数)=
.
开始
-1
3
-2
-2
3
-1
3
-2
1
考点讲练
核心知识点三
用频率估计概率
例5
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是(
)
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
考点讲练
例6
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数最有可能是(
)
A.24个
B.18个
C.16个
D.6个
C
考点讲练
针对训练
5.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球.如果口袋中装有3个红球且摸到红球的概率为
,那么口袋中球的总个数为_____.
解析:设口袋中球的总个数为x,
则摸到红球的概率为
,
所以x=15.
15
考点讲练
核心知识点四
用概率作决策
例6
在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
考点讲练
解:(1)列表如下
6
7
8
2
(6,2)
(7,2)
(8,2)
4
(6,4)
(7,4)
(8,4)
6
(6,6)
(7,6)
(8,6)
卡片
小球
共有9种等可能结果;
考点讲练
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
规则1:P(小红赢)=
;
规则2:P(小红赢)=
∵
,
∴小红选择规则1.
考点讲练
针对训练
6.A、B两个小型超市举行有奖促销活动,顾客每购满20元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同.规则是:
①A超市把转盘甲等分成4个扇形区域、B超市把转盘乙等分成3个扇形区域,并标上了数字(如图所示);
②顾客第一回转动转盘要转两次,第一次与第二次分别停止
后指针所指数字之和为奇数时
就获奖(若指针停在等分线上,
那么重转一次,直到指针指向
某一份为止).
1
1
2
2
3
3
4
甲
乙
考点讲练
解:(1)列表格如下:
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
第一回
第二回
甲转盘
共有16种等可能结果,其中中奖的有8种;
∴P(甲)=
(1)利用树形图或列表法分别求出A、B两超市顾客一回转盘获奖的概率;
考点讲练
1
2
3
1
2
3
4
2
3
4
5
3
4
5
6
第一回
第二回
乙转盘
∴P(乙)=
共有9种等可能结果,其中中奖的有4种;
考点讲练
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?说明理由.
(2)选甲超市.理由如下:
∵P(甲)>P(乙),
∴选甲超市.
知识小结
概率的进一步认识
简单的随机事件
复杂的随机事件
具有等可能性
不具有等可能性
树状图
列表
试验法
摸拟试验
理论计算
试验估算
概率定义
谢谢欣赏
THANK
YOU
FOR
LISTENING
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
