4.3.3余角与补角1
图片预览



文档简介
(共30张PPT)
1
2
比萨斜塔
1
2
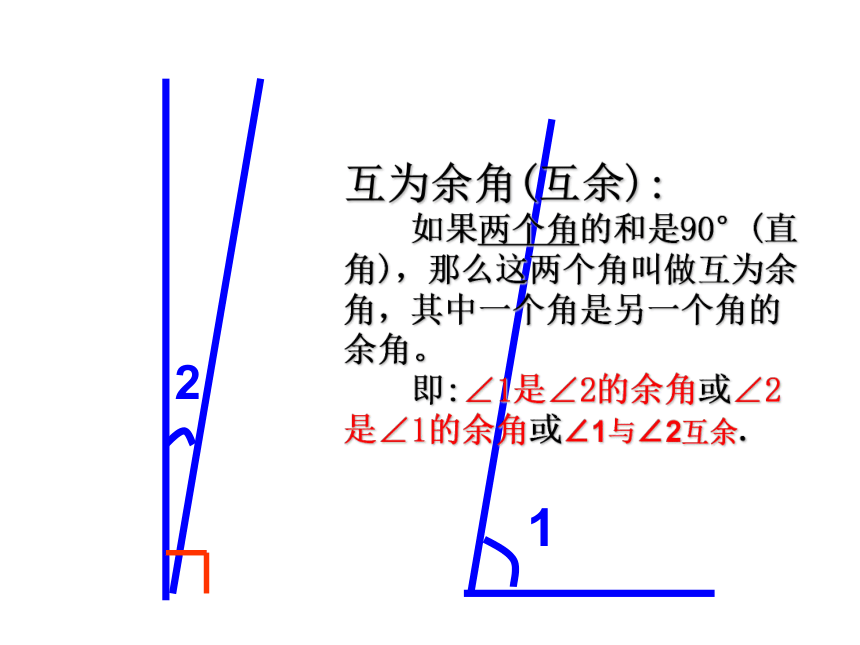
互为余角(互余):
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
即:∠1是∠2的余角或∠2是∠1的余角或∠1与∠2互余.
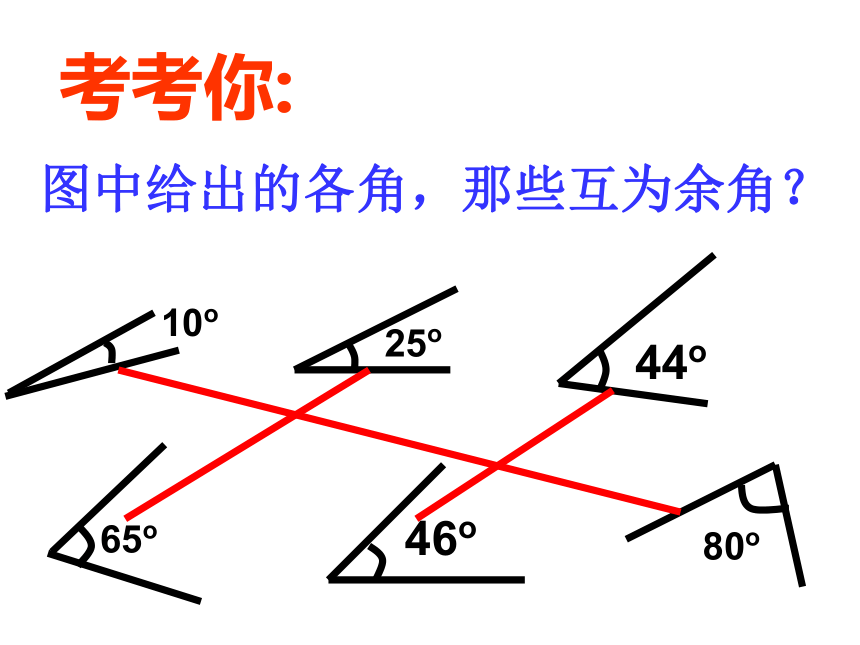
图中给出的各角,那些互为余角?
10o
25o
65o
80o
44o
46o
考考你:
3
4
比萨斜塔
4
3
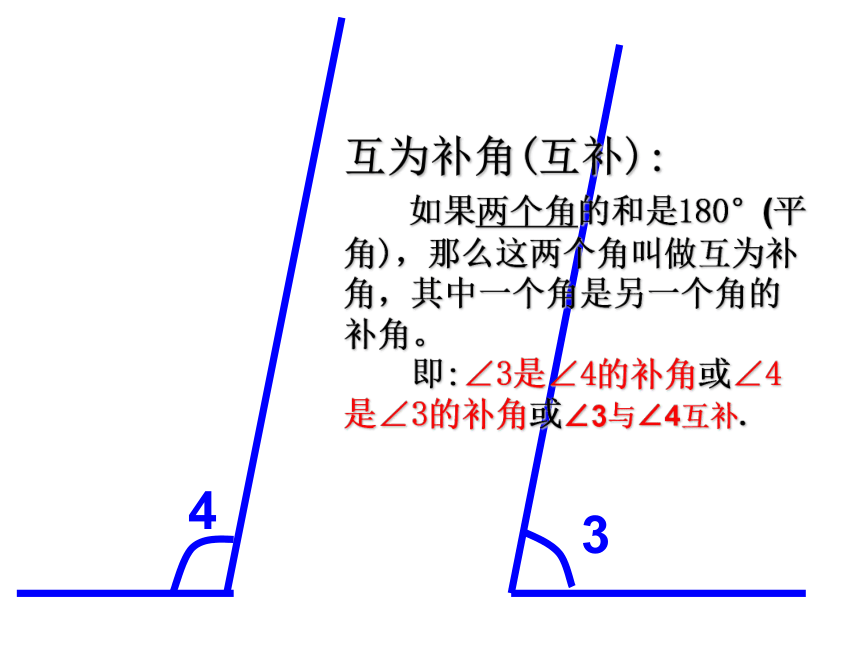
互为补角(互补):
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
即:∠3是∠4的补角或∠4是∠3的补角或∠3与∠4互补.
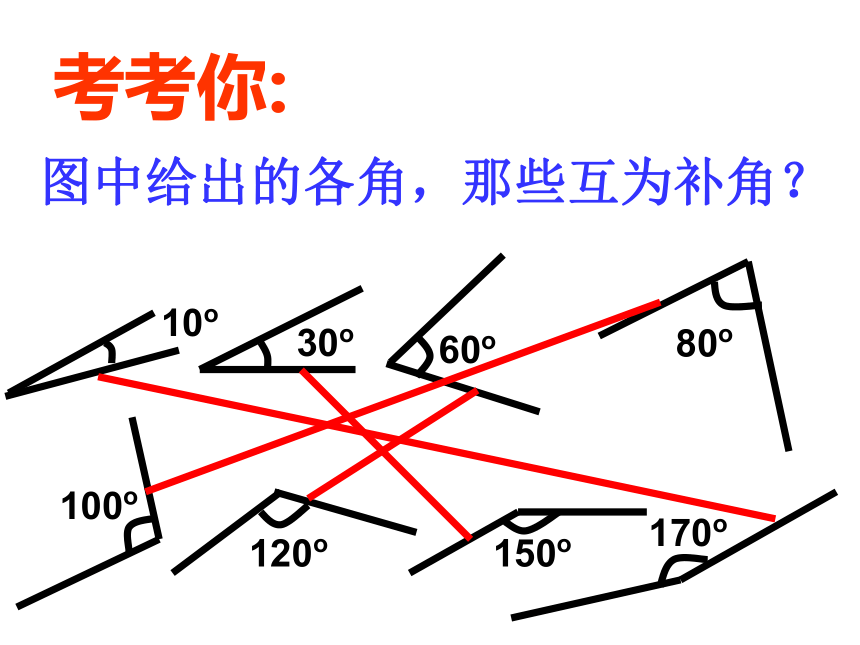
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
考考你:
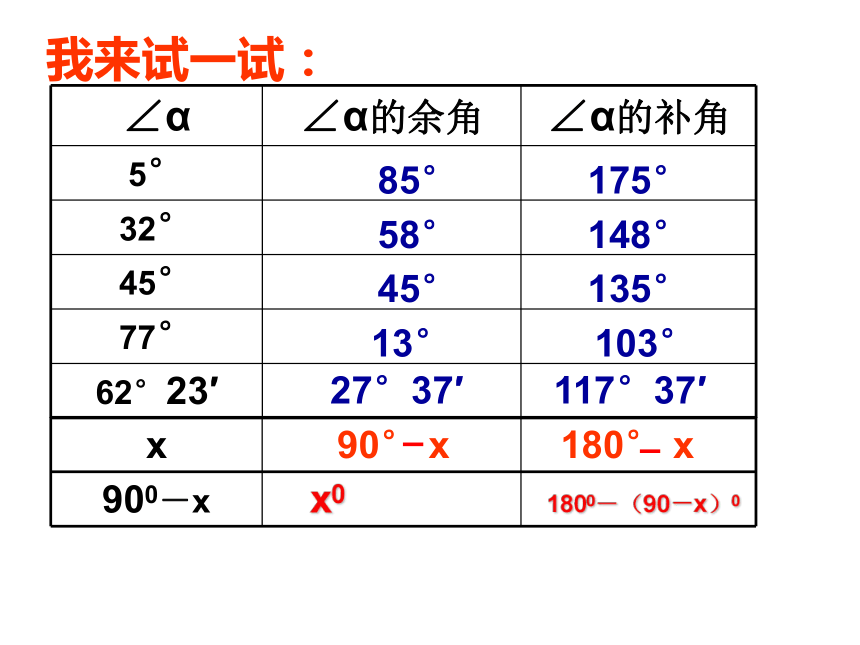
我来试一试:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x
900-x
90° x
180° x
x0
1800-(90-x)0
5) 30°的余角是_____,补角是______;若一个角的度数是x,
则它的余角的度数和补角的度数分别是__________,_________.
2)若∠1与∠2互补,则∠1+ ∠2=________.
3) ∠1= 180°-∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
90°- x
180°- x
1、抢答
反馈练习
1)已知∠1+∠2=90°则 ∠1 、∠2互为______.
4)已知∠A=50°,则∠A的余角是___ 补角是___ ,补角与余角的差是___.
余角
40°
130°
90°
1、90度的角叫余角,180度的角叫补角。 ( )
3、如果一个角有补角,那么这个角一定是钝角。( )
(一)判断题:
4、互补的两个角不可能相等。 ( )
5、钝角没有余角,但一定有补角。( )
6、互余的两个角一定都是锐角,两个锐角一定互余.( )
7、如果 。 ( )
2、若 ( )
8、如果 。( )
如图,C是直线AB上一点,CD是∠ACB的平分线
①图中互余的角有_______________________
②图中互补的角有_______________________
1
3
例:
若一个角的补角等于它的余角的4倍,求这个角的度数。
练习:
一个角的补角是它的3倍,这个角是多少度
练习:
1、一个角的补角是它的3倍,这个角是多少度
解:设这个角为x°,则它的补角为(180°-x°),得:
180 – x = 3 x
x = 45
答:这个角是45°。
你的点滴收获
本节课你学到了哪些知识?请你说一说.
互 余 互 补
数量关系
对
应
图
形
性
质
1、互余和互补
∠1+∠2=90°
∠1+∠2=180°
1
2
2
1
同角或等角的余角相等
同角或等角的补角相等
2、方位角
(1)方位角的表示
(2)方位角的特征
顶点是中心点
边:一边是南(北)线,另一边是视线
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:补角的性质
4
3
补角性质:
同角或等角的补角相等
1
4
2
探究:补角的性质
3
解:∵ ∠1 +∠2=180°, ∠3 +∠4=180°
∴ ∠2=180°-∠1 , ∠4=180°- ∠3
∵ ∠1 =∠3
∴ 180°-∠1 =180°- ∠3
即:∠2 =∠4
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:余角的性质
3
4
余角性质:
同角或等角的余角相等
探究:余角的性质
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解:∵ ∠1 +∠2=90°, ∠3 +∠4=90°
∴ ∠2=90°-∠1 , ∠4=90°- ∠3
∵ ∠1 =∠3
∴ 90°-∠1 =90°- ∠3
即:∠2 =∠4
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
甲地
乙地
乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
乙地对甲地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和蓝色线之间的角度
北
甲地
乙地
甲地对乙地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
甲地对乙地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
甲地对乙地的方位角
3.度量向南的射线和绿色线之间的角度
南
东
西
北
南
●
A
说出B在A的
B
●
40°
70°
●
B
65°
45°
●
B
●
B
那么A在B的
●
B
40°
北偏东40°
南偏西40°
例2:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
∴射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
1
2
比萨斜塔
1
2
互为余角(互余):
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
即:∠1是∠2的余角或∠2是∠1的余角或∠1与∠2互余.
图中给出的各角,那些互为余角?
10o
25o
65o
80o
44o
46o
考考你:
3
4
比萨斜塔
4
3
互为补角(互补):
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
即:∠3是∠4的补角或∠4是∠3的补角或∠3与∠4互补.
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
考考你:
我来试一试:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x
900-x
90° x
180° x
x0
1800-(90-x)0
5) 30°的余角是_____,补角是______;若一个角的度数是x,
则它的余角的度数和补角的度数分别是__________,_________.
2)若∠1与∠2互补,则∠1+ ∠2=________.
3) ∠1= 180°-∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
90°- x
180°- x
1、抢答
反馈练习
1)已知∠1+∠2=90°则 ∠1 、∠2互为______.
4)已知∠A=50°,则∠A的余角是___ 补角是___ ,补角与余角的差是___.
余角
40°
130°
90°
1、90度的角叫余角,180度的角叫补角。 ( )
3、如果一个角有补角,那么这个角一定是钝角。( )
(一)判断题:
4、互补的两个角不可能相等。 ( )
5、钝角没有余角,但一定有补角。( )
6、互余的两个角一定都是锐角,两个锐角一定互余.( )
7、如果 。 ( )
2、若 ( )
8、如果 。( )
如图,C是直线AB上一点,CD是∠ACB的平分线
①图中互余的角有_______________________
②图中互补的角有_______________________
1
3
例:
若一个角的补角等于它的余角的4倍,求这个角的度数。
练习:
一个角的补角是它的3倍,这个角是多少度
练习:
1、一个角的补角是它的3倍,这个角是多少度
解:设这个角为x°,则它的补角为(180°-x°),得:
180 – x = 3 x
x = 45
答:这个角是45°。
你的点滴收获
本节课你学到了哪些知识?请你说一说.
互 余 互 补
数量关系
对
应
图
形
性
质
1、互余和互补
∠1+∠2=90°
∠1+∠2=180°
1
2
2
1
同角或等角的余角相等
同角或等角的补角相等
2、方位角
(1)方位角的表示
(2)方位角的特征
顶点是中心点
边:一边是南(北)线,另一边是视线
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:补角的性质
4
3
补角性质:
同角或等角的补角相等
1
4
2
探究:补角的性质
3
解:∵ ∠1 +∠2=180°, ∠3 +∠4=180°
∴ ∠2=180°-∠1 , ∠4=180°- ∠3
∵ ∠1 =∠3
∴ 180°-∠1 =180°- ∠3
即:∠2 =∠4
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:余角的性质
3
4
余角性质:
同角或等角的余角相等
探究:余角的性质
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解:∵ ∠1 +∠2=90°, ∠3 +∠4=90°
∴ ∠2=90°-∠1 , ∠4=90°- ∠3
∵ ∠1 =∠3
∴ 90°-∠1 =90°- ∠3
即:∠2 =∠4
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
甲地
乙地
乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
乙地对甲地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和蓝色线之间的角度
北
甲地
乙地
甲地对乙地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
甲地对乙地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
甲地对乙地的方位角
3.度量向南的射线和绿色线之间的角度
南
东
西
北
南
●
A
说出B在A的
B
●
40°
70°
●
B
65°
45°
●
B
●
B
那么A在B的
●
B
40°
北偏东40°
南偏西40°
例2:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
∴射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
